【数据结构】二叉树 上篇
文章目录
- 二叉树的存储方式
- 二叉树的定义
- 常见的二叉树
-
- 满二叉树
- 完全二叉树
- 二叉搜索树
- 平衡二叉搜索树(AVL树)
- 红黑树
- 二叉树的遍历方式
-
- 深度优先(DFS)
- 广度优先(BFS)
- 二叉树的递归遍历
-
- leetcode144.二叉树的前序遍历
- leetcode145.二叉树的后序遍历
- leetcode94.二叉树的中序遍历
- 二叉树的迭代遍历
-
- 前序遍历
- 后序遍历
- 中序遍历
- 二叉树的统一迭代法遍历
-
- 前序遍历
- 后序遍历
- 中序遍历
- 二叉树的层序遍历
-
- leetcode102.二叉树的层序遍历
- leetcode199.二叉树的右视图
- leetcode637.二叉树的层平均值
- leetcode429.N 叉树的层序遍历
- leetcode515.在每个树行中找最大值
- leetcode116.填充每个节点的下一个右侧节点指针
- leetcode104.二叉树的最大深度
- leetcode111.二叉树的最小深度
- leetcode226.翻转二叉树
- leetcode101.对称二叉树
- leetcode100.相同的树
- leetcode572.另一个树的子树
- leetcode222.完全二叉树的节点个数
- leetcode110.平衡二叉树
二叉树的存储方式
二叉树可以顺序存储(用数组),也可以链式存储(用指针)。
顺序存储:如果父节点的数组下标是i,那么左子树就是2*i + 1,右子树是2*i + 2。
链式存储:

二叉树的定义
二叉树一般都选择用链式存储方式。其节点的定义如下:
struct TreeNode {
int val; // 节点值
TreeNode* left; // 左子树
TreeNode* right; // 右子树
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
}
二叉树节点的深度:从根节点到该节点的最长简单路径边的条数;(以节点为一度)
二叉树节点的高度:从该节点到叶子节点的最长简单路径边的条数。(以节点为一度)
常见的二叉树
满二叉树
满二叉树:深度为k,有2k-1个节点的二叉树
完全二叉树
完全二叉树:除了最底层节点可能没填满外,其余每层节点数都达到最大值,且最下面一层的节点都集中在该层最左边的若干位置。
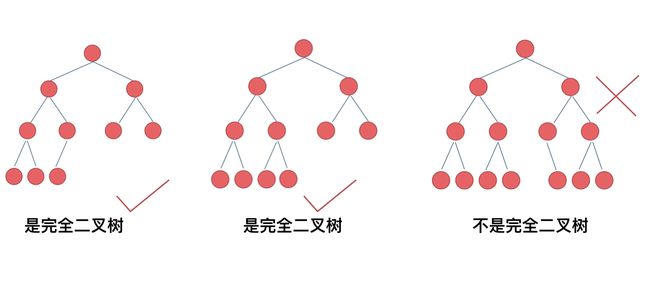
优先级队列其实是个堆,堆就是一颗完全二叉树,同时保证父子节点的顺序关系。
二叉搜索树
二叉搜索树的节点是有数值的,它是一个有序树。
平衡二叉搜索树(AVL树)
平衡二叉搜索树,简称平衡二叉树,又称为AVL树(Adelson-Velsky and Landis)。
它是一棵空树 或 它的左右两个子树的高度差的绝对值不超过1,且 左右两个子树都是一颗平衡二叉树。
AVL很严格,必须满足平衡条件,不管执行插入还是删除操作,只要不满足上面的条件,就要通过旋转来保持平衡,而旋转很耗时。
因此AVL树更适合用于查找多,插入/删除操作少的情况。

红黑树
红黑树是一种自平衡的二叉搜索树。
它在每个节点增加了一个存储位,用于表示节点的颜色,其颜色要求为:
- 每个节点非红即黑;
- 根节点必须是黑的;
- 红节点的两个子节点必须都是黑的;
- 任意节点到叶子节点的每条路径,经过的黑节点数目相同;
- 叶子节点(树尾端NULL指针或NULL节点)必须都是黑的;
C++中map、set、multimap、multiset的底层实现都是红黑树,其增删查找操作时间复杂度都是logn。
而unordered_map、unordered_set的底层实现是哈希表。
二叉树的遍历方式
深度优先(DFS)
先往深走,遇到叶子节点再往回走。
- 前序遍历:递归法、迭代法(栈)
- 中序遍历:递归法、迭代法(栈)
- 后序遍历:递归法、迭代法(栈)
广度优先(BFS)
一层一层的去遍历。
- 层序遍历:迭代法(队列)
栈其实是递归的一种实现结构,所以说前中后序遍历的逻辑其实都可以借助栈使用非递归的方式来实现;
而广度优先遍历的实现一般使用队列来实现,这是队列先进先出的特点所决定的,因为需要先进先出,才能一层一层的遍历二叉树。
二叉树的递归遍历
递归算法的三个要素:
- 确定递归函数的参数和返回值;
- 确定终止条件;
- 确定单层递归的逻辑。
leetcode144.二叉树的前序遍历
class Solution {
public:
void traversal(TreeNode* cur, vector<int>& vec) {
if(cur == nullptr) {
return;
}
vec.push_back(cur->val);
traversal(cur->left, vec);
traversal(cur->right, vec);
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> vec;
traversal(root, vec);
return vec;
}
};
leetcode145.二叉树的后序遍历
class Solution {
public:
void traversal(TreeNode* cur, vector<int>& vec) {
if(cur == nullptr) {
return;
}
traversal(cur->left, vec);
traversal(cur->right, vec);
vec.push_back(cur->val);
}
vector<int> postorderTraversal(TreeNode* root) {
vector<int> vec;
traversal(root, vec);
return vec;
}
};
leetcode94.二叉树的中序遍历
class Solution {
public:
void traversal(TreeNode* cur, vector<int>& vec) {
if(cur == nullptr) {
return;
}
traversal(cur->left, vec);
vec.push_back(cur->val);
traversal(cur->right, vec);
}
vector<int> inorderTraversal(TreeNode* root) {
vector<int> vec;
traversal(root, vec);
return vec;
}
};
二叉树的迭代遍历
递归的实现就是:每一次递归调用都把函数的局部变量、参数值和返回地址等压入调用栈中。然后递归返回的时候,从栈顶弹出上一次递归的各项参数,这就是递归为什么可以返回上一层位置的原因。
因此,用栈也可以实现二叉树的前中后序遍历。
前序遍历
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> vec;
stack<TreeNode*> st;
if(root == NULL) {
return vec;
}
st.push(root);
while(!st.empty()) {
TreeNode* tmpNode = st.top();
st.pop();
vec.push_back(tmpNode->val);
if(tmpNode->right) {
st.push(tmpNode->right);
}
if(tmpNode->left) {
st.push(tmpNode->left);
}
}
return vec;
}
};
后序遍历
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> vec;
stack<TreeNode*> st;
if(root == nullptr) {
return vec;
}
st.push(root);
while(!st.empty()) {
TreeNode* tmpNode = st.top();
st.pop();
vec.push_back(tmpNode->val);
if(tmpNode->left) {
st.push(tmpNode->left);
}
if(tmpNode->right) {
st.push(tmpNode->right);
}
}
reverse(vec.begin(), vec.end());
return vec;
}
};
中序遍历
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> vec;
stack<TreeNode*> st;
TreeNode* cur = root;
while(cur || !st.empty()) {
if(cur) {
st.push(cur);
cur = cur->left;
}
else {
cur = st.top();
st.pop();
vec.push_back(cur->val);
cur = cur->right;
}
}
return vec;
}
};
二叉树的统一迭代法遍历
使用栈:无法用时解决访问节点(遍历节点)和处理节点(将元素放进结果集)不一致的情况。
改进:将访问节点放入栈中,把要处理的节点也放入栈中,但是要做标记(紧接着放一个空指针作为标记)。
前序遍历
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> vec;
stack<TreeNode*> st;
if(root) {
st.push(root);
}
while(!st.empty()) {
TreeNode* tmpNode = st.top();
if(tmpNode) {
st.pop();
if(tmpNode->right) {
st.push(tmpNode->right); // 右
}
if(tmpNode->left) {
st.push(tmpNode->left); // 左
}
st.push(tmpNode); // 中
st.push(nullptr);
}
else { // 只有遇到空节点的时候,才将下一个节点放进结果集
st.pop();
tmpNode = st.top();
st.pop();
vec.push_back(tmpNode->val);
}
}
return vec;
}
};
后序遍历
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> vec;
stack<TreeNode*> st;
if(root) {
st.push(root);
}
while(!st.empty()) {
TreeNode* tmpNode = st.top();
if(tmpNode) {
st.pop();
st.push(tmpNode); // 中
st.push(nullptr);
if(tmpNode->right) {
st.push(tmpNode->right); // 右
}
if(tmpNode->left) {
st.push(tmpNode->left); // 左
}
}
else { // 只有遇到空节点的时候,才将下一个节点放进结果集
st.pop();
tmpNode = st.top();
st.pop();
vec.push_back(tmpNode->val);
}
}
return vec;
}
};
中序遍历
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> vec;
stack<TreeNode*> st;
if(root) {
st.push(root);
}
while(!st.empty()) {
TreeNode* tmpNode = st.top();
if(tmpNode) {
st.pop();
if(tmpNode->right) {
st.push(tmpNode->right); // 右
}
st.push(tmpNode); // 中
st.push(nullptr);
if(tmpNode->left) {
st.push(tmpNode->left); // 左
}
}
else { // 只有遇到空节点的时候,才将下一个节点放进结果集
st.pop();
tmpNode = st.top();
st.pop();
vec.push_back(tmpNode->val);
}
}
return vec;
}
};
二叉树的层序遍历
层序遍历:逐层地,从左到右访问所有节点。
二叉树的层序遍历就是图论中的广度优先搜索在二叉树中的应用,用队列实现。
leetcode102.二叉树的层序遍历
// BFS
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> result;
queue<TreeNode*> que;
if(root) que.push(root);
while(!que.empty()) {
int sz = que.size();
vector<int> vec;
for(int i = 0; i < sz; i++) {
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
result.push_back(vec);
}
return result;
}
};
// DFS
class Solution {
public:
void dfs(TreeNode* cur, vector<vector<int>>& result, int depth) {
if(!cur) {
return;
}
if(result.size() == depth) {
result.push_back(vector<int>());
}
result[depth].push_back(cur->val);
dfs(cur->left, result, depth + 1);
dfs(cur->right, result, depth + 1);
}
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> result;
int depth = 0;
dfs(root, result, depth);
return result;
}
};
leetcode199.二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
vector<int> result;
queue<TreeNode*> que;
if(root) que.push(root);
while(!que.empty()) {
int sz = que.size();
result.push_back(que.back()->val);
while(sz--) {
TreeNode* node = que.front();
que.pop();
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
}
return result;
}
};
leetcode637.二叉树的层平均值
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。
class Solution {
public:
vector<double> averageOfLevels(TreeNode* root) {
vector<double> result;
queue<TreeNode*> que;
if(root) que.push(root);
while(!que.empty()) {
int sz = que.size();
double sum = 0;
while(sz--) {
TreeNode* node = que.front();
que.pop();
sum += node->val;
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
result.push_back(sum/sz);
}
return result;
}
};
leetcode429.N 叉树的层序遍历
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
vector<vector<int>> result;
queue<Node*> que;
if(root) que.push(root);
while(!que.empty()) {
int sz = que.size();
vector<int> vec;
while(sz--) {
Node* node = que.front();
que.pop();
vec.push_back(node->val);
for(int i = 0; i < node->children.size(); i++) {
if(node->children[i]) que.push(node->children[i]);
}
}
result.push_back(vec);
}
return result;
}
};
leetcode515.在每个树行中找最大值
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
class Solution {
public:
vector<int> largestValues(TreeNode* root) {
vector<int> result;
queue<TreeNode*> que;
if(root) que.push(root);
while(!que.empty()) {
int sz = que.size();
int max = INT_MIN;
while(sz--) {
TreeNode* node = que.front();
que.pop();
max = node->val > max ? node->val : max;
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
result.push_back(max);
}
return result;
}
};
leetcode116.填充每个节点的下一个右侧节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> que;
if(root) que.push(root);
while(!que.empty()) {
int sz = que.size();
Node* node = NULL;
for(int i = 0; i < sz; i++) {
node = que.front();
que.pop();
node->next = que.front();
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
node->next = NULL;
}
return root;
}
};
leetcode104.二叉树的最大深度
// 递归法
class Solution {
public:
int maxDepth(TreeNode* root) {
if(!root) {
return 0;
}
int left = maxDepth(root->left);
int right = maxDepth(root->right);
return max(left, right) + 1;
}
};
// 迭代法
class Solution {
public:
int maxDepth(TreeNode* root) {
int result = 0;
queue<TreeNode*> que;
if(root) que.push(root);
while(!que.empty()) {
int sz = que.size();
result++;
while(sz--) {
TreeNode* node = que.front();
que.pop();
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
}
return result;
}
};
leetcode111.二叉树的最小深度
// 递归法
class Solution {
public:
int minDepth(TreeNode* root) {
if(!root) {
return 0;
}
int left = minDepth(root->left);
int right = minDepth(root->right);
if(!root->left && root->right) {
return right + 1;
}
if(root->left && !root->right) {
return left + 1;
}
return min(left, right) + 1;
}
};
// 迭代法
class Solution {
public:
int minDepth(TreeNode* root) {
int result = 0;
queue<TreeNode*> que;
if(root) que.push(root);
while(!que.empty()) {
int sz = que.size();
result++;
while(sz--) {
TreeNode* node = que.front();
que.pop();
if(!node->left && !node->right) {
return result;
}
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
}
return result;
}
};
leetcode226.翻转二叉树
// 递归,前序遍历
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root == nullptr) {
return root;
}
swap(root->left, root->right);
invertTree(root->left);
invertTree(root->right);
return root;
}
};
// 统一迭代,前序遍历
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
stack<TreeNode*> st;
if(root) st.push(root);
while(!st.empty()) {
TreeNode* node = st.top();
if(node) {
st.pop();
if(node->right) st.push(node->right);
if(node->left) st.push(node->left);
st.push(node);
st.push(nullptr);
}
else {
st.pop();
node = st.top();
st.pop();
swap(node->right, node->left);
}
}
return root;
}
};
// 迭代,层序遍历
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
queue<TreeNode*> que;
if(root) que.push(root);
while(!que.empty()) {
int sz = que.size();
while(sz--) {
TreeNode* node = que.front();
que.pop();
swap(node->left, node->right);
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
}
return root;
}
};
leetcode101.对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
// 递归法
class Solution {
public:
bool compare(TreeNode* left, TreeNode* right) {
if((!left && right) || (left && !right)) {
return false;
}
if(!left && !right) {
return true;
}
if(left->val != right->val) {
return false;
}
return compare(left->left, right->right) && compare(left->right, right->left);
}
bool isSymmetric(TreeNode* root) {
if(root == nullptr) return true;
return compare(root->left, root->right);
}
};
//迭代法,此处的stack换成queue也同样可以
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(!root) return true;
stack<TreeNode*> st;
st.push(root->left);
st.push(root->right);
while(!st.empty()) {
TreeNode* leftnode = st.top();
st.pop();
TreeNode* rightnode = st.top();
st.pop();
if(!leftnode && !rightnode) {
continue;
}
if(!leftnode || !rightnode || (leftnode->val != rightnode->val)) {
return false;
}
st.push(leftnode->left);
st.push(rightnode->right);
st.push(leftnode->right);
st.push(rightnode->left);
}
return true;
}
};
leetcode100.相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
// 递归法
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if(!p && !q) {
return true;
}
if(!p || !q || (p->val != q->val)) {
return false;
}
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
};
// 迭代法
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
queue<TreeNode*> que;
que.push(p);
que.push(q);
while(!que.empty()) {
TreeNode* pp = que.front();
que.pop();
TreeNode* qq = que.front();
que.pop();
if(!pp && !qq) {
continue;
}
if(!pp || !qq || (pp->val != qq->val)) {
return false;
}
que.push(pp->left);
que.push(qq->left);
que.push(pp->right);
que.push(qq->right);
}
return true;
}
};
leetcode572.另一个树的子树
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
// 递归法
class Solution {
public:
bool compare(TreeNode* p, TreeNode* q) {
if(!p && !q) {
return true;
}
if(!p || !q || (p->val != q->val)) {
return false;
}
return compare(p->left, q->left) && compare(p->right, q->right);
}
bool isSubtree(TreeNode* root, TreeNode* subRoot) {
if(!root && !subRoot) {
return true;
}
if(!root) {
return false;
}
return compare(root, subRoot) || isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}
};
leetcode222.完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
// 适用于所有二叉树
class Solution {
public:
int countNodes(TreeNode* root) {
if(!root) return 0;
int result = 0;
queue<TreeNode*> que;
que.push(root);
while(!que.empty()) {
TreeNode* node = que.front();
que.pop();
result++;
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
return result;
}
};
// 针对完全二叉树
class Solution {
public:
int countNodes(TreeNode* root) {
if(!root) return 0;
int leftlen = 0;
int rightlen = 0;
TreeNode* left = root->left;
TreeNode* right = root->right;
while(left) {
left = left->left;
leftlen++;
}
while(right) {
right = right->right;
rightlen++;
}
if(leftlen == rightlen) {
return (2 << leftlen) - 1;
}
return countNodes(root->left) + countNodes(root->right) + 1;
}
};
leetcode110.平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
class Solution {
public:
int getHeight(TreeNode* node) {
if (!node) return 0;
int leftHeight = getHeight(node->left);
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right);
if (rightHeight == -1) return -1;
return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
}
bool isBalanced(TreeNode* root) {
return getHeight(root) == -1 ? false : true;
}
};