数据结构——快速排序(hoare版、挖坑法、前后指针版、循环实现)
目录
一、算法思想
1.hoare版
2.挖坑法
3.前后指针版
二、算法缺陷与优化
1.算法缺陷
1.1基准值取值
1.2递归超限
2.优化方法
2.1三位取中法
2.2设置阈值
2.3循环实现
三、接口实现
1.快速排序
2.hoare版
3.挖坑法
4.前后指针版
5.非递归版
四、接口测试
1.测试用例
2.测试结果
2.1递归方式
2.2非递归方式
五、性能分析
六、完整代码
1.QuickSort.c
2.Stack.h
一、算法思想
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想是:任意选取待排序序列中的一个元素作为基准值,按照该排序码将待排序集合分割成两个子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后再对左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
注:后续实现均以取序列最右侧元素为基准值为例。
其中,将区间按照基准值划分为左右两部分的常见方式有三种:
1.hoare版
通过两个标志,分别从左往右找比基准值大的元素和从右向左找比基准值小的元素,然后交换两个元素,重复上述过程直到两个标志位相遇,最后再将基准值交换到相遇位置,然后再对左右子序列重复上述过程,直到整个序列完成排序。
图示:
2.挖坑法
挖坑法大体思路与hoare法思路相同,其基本思想是:将基准值保存到标记位中,这样最右侧位置就形成了一个坑位,然后左侧标注位往右遍历找比基准值大的元素,找到后将该元素填入右侧坑位中,该位置就又形成了一个新的坑位,然后从右侧往左遍历找比基准值小的元素,将该元素填入到坑位中,重复上述过程直到左右标志位相遇,最后将基准值放入最后的坑位中,最对左右子序列重复上述过程直到整个序列排序完成。
图示基准值取的为最左侧元素:
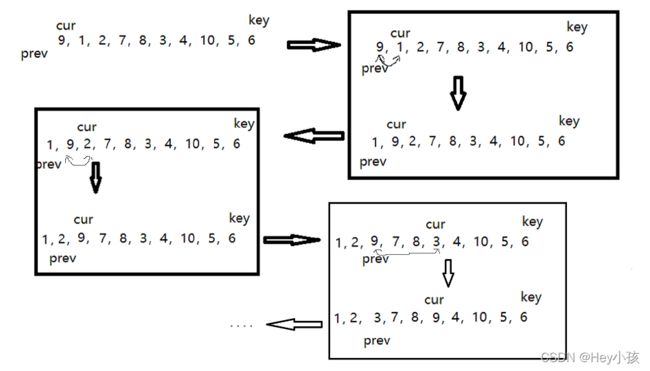
3.前后指针版
初始设置cur、prev两个标志指针,cur标志序列第一个元素,prev标志cur前一个位置,cur位置的元素若大于基准值,cur向前前进,若小于基准值,则先对prev进行加一,然后交换cur和prev标记位置的元素,这样就能保证cur与prev之间的元素都大于基准值,prev之前的元素都小于基准值,重复上述过程,直到cur超过序列最右侧位置,最后进行一次判断,若prev标记位置不是序列最后一个位置,则将基准值交换到prev交换位置,即完成左右子序列划分,再对左右子序列重复上述过程,直到整个序列完成排序。
图示:
二、算法缺陷与优化
1.算法缺陷
1.1基准值取值
若所取基准值为序列中的最大或最小值,那么每趟划分后,基准值的一侧将会出现没有元素的情况,就相当于每趟只完成了一个元素的排序,那么快速排序的时间复杂度此时将达到![]() ,效率较低。
,效率较低。
1.2递归超限
算法递归深度会随着元素的增多而加深,若序列元素元素量非常巨大,可能会造成递归超限。
2.优化方法
2.1三位取中法
我们可以通过选取序列中开始、中间、末尾三个位置中元素大小居中的元素作为基准值,此方法可以大大降低基准值取到序列内最大或最小元素的概率。
注:为了不改变代码的逻辑实现,若取得的基准值的位置不是基准值默认位置,可先提前将基准值交换到所取基准值的默认位置处。
2.2设置阈值
我们可以发现,随着划分次数的增加,子序列内的元素个数会不断减少,而且元素数量较少时,各类排序算法的效率差距其实是可以忽略不记的,而比较适合元素个数比较少的排序就是直接插入排序,所以我们可以在递归的过程中设计一个阈值,当子序列中元素个数不超过阈值时,递归不再进行,而是直接对当前子序列进行直接插入排序,然后返回。
当然,这种方法只能进行一定程度的缓解,并不能完全解决递归超限的问题。
所以,我们可以提前估算一下递归的深度N,再在递归深度上设置一个阈值count,若N小于count直接进行快速排序;若N大于count,先通过快速排序递归count次,然后再对每个分组中进行其他排序(比如:堆排序)。
这样即不会对算法效率造成太大影响,也避免了递归超限的问题。
2.3循环实现
使用循环的方式实现快速排序,我们会发现直接转循环并不容易实现,结合递归调用的特性,后调用的先结束退出,先调用的后结束,符合栈后进先出的特点,所有可以利用栈来循环实现快速排序。
每次对序列进行分割后,利用栈依次压入左右子序列的右边界和左边界,这样下一次循环就会依次拿到一个子序列的左右边界,然后再对此序列进行分割,循环进行上述操作,直到栈为空即完成序列排序。(可加上优化方法,为子序列元素个数加上阈值)
三、接口实现
1.快速排序
void QuickSort(int* array, int left, int right) {//快速排序
if (right - left <= 16) {//阈值设置为16
InsertSort(array + left, right - left);//达到阈值,进行直接插入排序
}
else {
if (right - left <= 1) {//区间内少于等于1个元素,不需要再排
return;
}
int div = PartSort2(array, left, right);//找一个基准值对区间元素进行划分,分割完成后返回基准值位置
QuickSort(array, left, div);//对基准值左侧进行快排
QuickSort(array, div + 1, right);//对基准值右侧进行快排
}
}2.hoare版
int PartSort1(int* array, int left, int right) {//快速排序hoare版
int begin = left;
int end = right - 1;
int midPos = GetMiddleIndex(array, left, right);//获取元素大小相对靠中的元素下标
if (midPos != end) {//将该元素交换到末尾,从而不影响后续代码的逻辑实现
Swap(&array[midPos], &array[end]);
}
int key = array[end];//取最后一个元素为基准值
while (begin < end) {//begin与end没有相遇
while (begin < end && array[begin] <= key) {//1.从前往后找比基准值key大的元素
begin++;
}
while (begin < end && array[end] >= key) {//2.从后往前找比基准值key小的元素
end--;
}
if (begin != end) {//3.交换两个元素
Swap(&array[begin], &array[end]);
}
}
Swap(&array[begin], &array[right - 1]);//4.将基准值交换到区间中间位置
return begin;//5.返回基准值下标
}3.挖坑法
int PartSort2(int* array, int left, int right) {//快速排序挖坑法
int begin = left;
int end = right - 1;
int midPos = GetMiddleIndex(array, left, right);//获取元素大小相对靠中的元素下标
if (midPos != end) {//将该元素交换到末尾,从而不影响后续代码的逻辑实现
Swap(&array[midPos], &array[end]);
}
int key = array[end];//1.取最后一个元素为基准值,并挖坑end
while (begin < end) {//begin与end没有相遇
while (begin < end && array[begin] <= key) {//2.从前往后找比基准值key大的元素
begin++;
}
if (begin != end) {
array[end--] = array[begin];//3.填end坑,挖begin坑,end前移一位
}
while (begin < end && array[end] >= key) {//4.从后往前找比基准值key小的元素
end--;
}
if (begin != end) {
array[begin++] = array[end];//5.填begin坑,挖end坑,begin后移一位
}
}
array[end] = key;//6.基准值放入最后一个坑内
return end;//7.返回基准值下标
}4.前后指针版
int PartSort3(int* array, int left, int right) {//快速排序前后指针版
int cur = left;//标记第一个元素
int prev = cur - 1;//位于cur之后一个位置
int midPos = GetMiddleIndex(array, left, right);//获取元素大小相对靠中的元素下标
if (midPos != right - 1) {//将该元素交换到末尾,从而不影响后续代码的逻辑实现
Swap(&array[midPos], &array[right - 1]);
}
int key = array[right - 1];//取最后一个元素为基准值
while (cur < right) {
if (array[cur] < key && ++prev != cur) {//始终保存cur与prev之间的元素都大于基准值key
Swap(&array[cur], &array[prev]);
}
cur++;
}
if (++prev != right - 1) {//将基准值交换到prev的下一个位置
Swap(&array[right - 1], &array[prev]);
}
return prev;
}5.非递归版
void QuickSortNonR(int* array, int size) {//快速排序非递归版
Stack s;
StackInit(&s);
int left = 0;
int right = size;
StackPush(&s, right);//依次压入右边界和左边界
StackPush(&s, left);
while (!StackEmpty(&s)) {//栈不为空,循环进行
left = StackTop(&s);//获取栈顶,左边界
StackPop(&s);//左边界出栈
right = StackTop(&s);//获取栈顶,右边界
StackPop(&s);//右边界出栈
if (right - left <= 16) {//子序列达到阈值
InsertSort(array + left, right - left);//进行直接插入排序
}
else {
int div = PartSort2(array, left, right);
//基准值左侧(left,div);右侧(div+1,right)
//先压右侧子序列边界(先压右边界,再压左边界)
StackPush(&s, right);
StackPush(&s, div + 1);
//再压左侧子序列边界
StackPush(&s, div);
StackPush(&s, left);
}
}
}四、接口测试
1.测试用例
void TestPartSort() {//快速排序测试函数
int array[] = { 5,4,8,1,9,7,3,2,6,0 };
int length = sizeof(array) / sizeof(array[0]);
printf("排序前:");
PrintArray(array, length);
QuickSort(array, 0, length);//递归方式
//QuickSortNonR(array, length);//非递归方式
printf("\n排序后:");
PrintArray(array, length);
}2.测试结果
2.1递归方式
2.2非递归方式
五、性能分析
1.时间复杂度:![]()
2.空间复杂度:![]()
3.稳定性:不稳定
六、完整代码
1.QuickSort.c
#include"Stack.h"
void QuickSort(int* array, int left, int right);//快速排序
int PartSort1(int* array, int left, int right);//快速排序hoare版
int PartSort2(int* array, int left, int right);//快速排序挖坑法
int PartSort3(int* array, int left, int right);//快速排序前后指针版
int GetMiddleIndex(int* array, int left, int right);//三位取中法(选取元素大小相对靠中的为基准值)
void QuickSortNonR(int* array, int size);//快速排序非递归版
void InsertSort(int* array, int size);//直接插入排序
void PrintArray(int* array, int size);//数组打印
void Swap(int* num1, int* num2);//整数交换
void TestPartSort();//快速排序测试函数
int main() {
TestPartSort();
return 0;
}
void QuickSort(int* array, int left, int right) {//快速排序
if (right - left <= 16) {//阈值设置为16
InsertSort(array + left, right - left);//达到阈值,进行直接插入排序
}
else {
if (right - left <= 1) {//区间内少于等于1个元素,不需要再排
return;
}
int div = PartSort2(array, left, right);//找一个基准值对区间元素进行划分,分割完成后返回基准值位置
QuickSort(array, left, div);//对基准值左侧进行快排
QuickSort(array, div + 1, right);//对基准值右侧进行快排
}
}
int PartSort1(int* array, int left, int right) {//快速排序hoare版
int begin = left;
int end = right - 1;
int midPos = GetMiddleIndex(array, left, right);//获取元素大小相对靠中的元素下标
if (midPos != end) {//将该元素交换到末尾,从而不影响后续代码的逻辑实现
Swap(&array[midPos], &array[end]);
}
int key = array[end];//取最后一个元素为基准值
while (begin < end) {//begin与end没有相遇
while (begin < end && array[begin] <= key) {//1.从前往后找比基准值key大的元素
begin++;
}
while (begin < end && array[end] >= key) {//2.从后往前找比基准值key小的元素
end--;
}
if (begin != end) {//3.交换两个元素
Swap(&array[begin], &array[end]);
}
}
Swap(&array[begin], &array[right - 1]);//4.将基准值交换到区间中间位置
return begin;//5.返回基准值下标
}
int PartSort2(int* array, int left, int right) {//快速排序挖坑法
int begin = left;
int end = right - 1;
int midPos = GetMiddleIndex(array, left, right);//获取元素大小相对靠中的元素下标
if (midPos != end) {//将该元素交换到末尾,从而不影响后续代码的逻辑实现
Swap(&array[midPos], &array[end]);
}
int key = array[end];//1.取最后一个元素为基准值,并挖坑end
while (begin < end) {//begin与end没有相遇
while (begin < end && array[begin] <= key) {//2.从前往后找比基准值key大的元素
begin++;
}
if (begin != end) {
array[end--] = array[begin];//3.填end坑,挖begin坑,end前移一位
}
while (begin < end && array[end] >= key) {//4.从后往前找比基准值key小的元素
end--;
}
if (begin != end) {
array[begin++] = array[end];//5.填begin坑,挖end坑,begin后移一位
}
}
array[end] = key;//6.基准值放入最后一个坑内
return end;//7.返回基准值下标
}
int PartSort3(int* array, int left, int right) {//快速排序前后指针版
int cur = left;//标记第一个元素
int prev = cur - 1;//位于cur之后一个位置
int midPos = GetMiddleIndex(array, left, right);//获取元素大小相对靠中的元素下标
if (midPos != right - 1) {//将该元素交换到末尾,从而不影响后续代码的逻辑实现
Swap(&array[midPos], &array[right - 1]);
}
int key = array[right - 1];//取最后一个元素为基准值
while (cur < right) {
if (array[cur] < key && ++prev != cur) {//始终保存cur与prev之间的元素都大于基准值key
Swap(&array[cur], &array[prev]);
}
cur++;
}
if (++prev != right - 1) {//将基准值交换到prev的下一个位置
Swap(&array[right - 1], &array[prev]);
}
return prev;
}
void QuickSortNonR(int* array, int size) {//快速排序非递归版
Stack s;
StackInit(&s);
int left = 0;
int right = size;
StackPush(&s, right);//依次压入右边界和左边界
StackPush(&s, left);
while (!StackEmpty(&s)) {//栈不为空,循环进行
left = StackTop(&s);//获取栈顶,左边界
StackPop(&s);//左边界出栈
right = StackTop(&s);//获取栈顶,右边界
StackPop(&s);//右边界出栈
if (right - left <= 16) {//子序列达到阈值
InsertSort(array + left, right - left);//进行直接插入排序
}
else {
int div = PartSort2(array, left, right);
//基准值左侧(left,div);右侧(div+1,right)
//先压右侧子序列边界(先压右边界,再压左边界)
StackPush(&s, right);
StackPush(&s, div + 1);
//再压左侧子序列边界
StackPush(&s, div);
StackPush(&s, left);
}
}
}
int GetMiddleIndex(int* array, int left, int right) {//三位取中法(选取元素大小相对靠中的为基准值)
int mid = (left + right) / 2;
//返回基准值的下标
if (array[left] < array[right - 1]) {
if (array[mid] < array[left]) {
return left;
}
else if (array[mid] > array[right - 1]) {
return right - 1;
}
else {
return mid;
}
}
else {//array[left]>=array[right-1]
if (array[mid] > array[left]) {
return left;
}
else if (array[mid] < array[right - 1]) {
return right - 1;
}
else {
return mid;
}
}
}
void InsertSort(int* array, int size) {//直接插入排序
for (int i = 1; i < size; i++) {//从1开始循环,默认数组内第一个元素为有序序列
int end = i - 1;//标记已排序序列最后位置下标
int key = array[i];//依次拿取数组内元素
while (end >= 0 && key < array[end]) {//key从前往后比较:小于当前元素,继续往前走
array[end + 1] = array[end];//将当前元素往后移一个位置
end--;
}
array[end + 1] = key;//key大于等于当前元素,插入到当前位置之后
}
}
void PrintArray(int* array, int size) {//数组打印
for (int i = 0; i < size; i++) {
printf("%d ", array[i]);
}
}
void Swap(int* num1, int* num2) {//整数交换
int temp = *num1;
*num1 = *num2;
*num2 = temp;
}
void TestPartSort() {//快速排序测试函数
int array[] = { 5,4,8,1,9,7,3,2,6,0 };
int length = sizeof(array) / sizeof(array[0]);
printf("排序前:");
PrintArray(array, length);
//QuickSort(array, 0, length);//递归方式
QuickSortNonR(array, length);//非递归方式
printf("\n排序后:");
PrintArray(array, length);
}2.Stack.h
#pragma once
#include
#include
#include
#include
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack
{
STDataType* array;
int top; // 栈顶
int capacity; // 容量
}Stack;
/*void StackInit(Stack* ps, int capacity);// 初始化栈
void StackPush(Stack* ps, STDataType data);// 入栈
void StackPop(Stack* ps);// 出栈
STDataType StackTop(Stack* ps);// 获取栈顶元素
int StackSize(Stack* ps);// 获取栈中有效元素个数
int StackEmpty(Stack* ps);// 检测栈是否为空,为空返回1,非空返回0
void StackDestroy(Stack* ps);// 销毁栈
void Stack_Test();//功能测试函数
*/
// 初始化栈
void StackInit(Stack* ps) {
assert(ps);
ps->array = (STDataType*)malloc(sizeof(STDataType) * 3);
if (ps->array == NULL) {//申请失败
assert(0);
return;
}
ps->capacity = 3;
ps->top = 0;
}
void StackCheckCapacity(Stack* ps) {
assert(ps);
if (ps->top == ps->capacity) {//栈满
int newCapacity = ps->capacity * 2;//每次扩容扩大两倍
STDataType* temp = (STDataType*)malloc(sizeof(STDataType) * newCapacity);//开辟新空间
if (temp == NULL) {
assert(0);
return;
}
memcpy(temp, ps->array, sizeof(STDataType) * ps->capacity);//将元数据拷贝到新空间中
free(ps->array);//释放旧空间,使用新空间
ps->array = temp;
ps->capacity = newCapacity;
}
}
void StackPush(Stack* ps, STDataType data) {//入栈
StackCheckCapacity(ps);//判断是否栈满,栈满则扩容
ps->array[ps->top] = data;
ps->top++;
}
int StackEmpty(Stack* ps) {//栈判空
assert(ps);
return 0 == ps->top;//空返回1,非空返回0
}
void StackPop(Stack* ps) {//出栈
if (StackEmpty(ps)) {//判空
return;
}
ps->top--;
}
STDataType StackTop(Stack* ps) {//获取栈顶元素
assert(ps);
return ps->array[ps->top - 1];
}
int StackSize(Stack* ps) {//获取栈中有效元素个数
assert(ps);
return ps->top;
}
void StackDestroy(Stack* ps) {//栈销毁
assert(ps);
if (ps->array) {
free(ps->array);
ps->capacity = 0;
ps->top = 1;
}
}