小样本学习FSL介绍

1 概念

小样本学习（few-shot learning，FSL）旨在从有限的标记实例（通常只有几个）中学习，并对新的、未见过的实例进行识别。
相比于传统的深度学习和机器学习方法，小样本学习能够更好地模拟人类的学习方式，因为人类在学习新事物时通常只需要很少的示例即可，即从人工智能到人类智能转变。

首先，在FSL设置中，通常有三组数据集，包括支持集S、查询集Q和辅助集A。S中的实例类别已知，Q中实例类别未知但一定属于S，S和A的实例类别一定不相交，即S中的类别一定不会出现在A中。

FSL任务通常被设定为 N-way K-shot 的形式，其中N是类别的数量，K是每个类别中标记的样本数量，表示支持集 S 有N个类，每个类有K个标记样本。N通常设为5，K通常设为1或5。用符号表示：

1. 辅助集(或基类集) $A={\left\{X_i,y_i\right\}}_{i=1}^M$ ，其中图像 $X_i\in {\mathbb{R}}^{H\times W\times 3}$ ， one-hot 标签向量$y_i\in Y={\left\{0,1\right\}}^{C_{base}}$
2. 支持集 $S=\left\{S_1,\cdot \cdot \cdot ,S_N\right\}={\left\{X_i,y_i\right\}}_{i=1}^{NK}$ , 其中 $S_N={\left\{X_i,y_N\right\}}_{i=1}^K$ 包含 K 幅图像并且是 S 中的第 N 类。
3. 查询集 $Q={\left\{Qi,yi\right\}}_{i=1}^{NM}$，其中M通常设为15。

每个类别中如此少的标记样本几乎不可能训练出有效的分类模型，因此，FSL 的一个解决方案就是如何使用 A 来促进对目标任务（即 S 和 Q）的学习。好处是 A 通常比 S 拥有更多的类和每个类的样本，而挑战是 A 与 S 有一个不相交的标签空间，甚至可能与 S 有很大的域偏差。

通常FSL将 数据集D 分为$D_{train}、D_{val}和D_{test}$，分别进行训练、验证和测试。$D_{train}$作为辅助集A，然后分别从$D_{val}和D_{test}$中随机抽样形成大量评估任务 T。

为了学习有效的 FSL 模型，通常在训练阶段采用 Episodic-training策略（元训练范式），它依赖于 大量模拟的few-shot任务（即元任务） ，这些任务是从 辅助集A 中随机构建。一个模拟任务 T 由两个子集组成，$A_S和A_Q$，分别对应于支持集S和查询集Q 。具体来说，训练时的一个epoch当中有大量episodes，每个episode对应一个元任务，通过构建的大量元任务训练模型。在FSL设置中batch_size就相当于每次将几个元任务送入模型，如果batch_size=4，表示一次将4个元任务送入模型来训练。用符号表示：

1. 我们要从任务分布 ρ(T)中随机取样大量任务来训练模型，即 ${\left\{{\mathcal{T}}^i=⟨{\mathcal{A}}_{\mathcal{S}}^i,{\mathcal{A}}_{\mathcal{Q}}^i⟩\right\}}_{i=1}^{\mathcal{M}}\in \rho (\mathcal{T})$
2. 在每次迭代(epoch)中，通过大量模拟任务（episode）$T=⟨{\mathcal{A}}_{\mathcal{S}},{\mathcal{A}}_{\mathcal{Q}}⟩$ 来训练当前模型。

此外，接下来文中出现的 $f_{\theta }(\cdot )和g_{\omega }(\cdot )$ 分别表示嵌入主干（CNN或Transfomrer）和分类器。此外， $f_{\theta }(\cdot )和g_{\omega }(\cdot )$ 可以集成到同一个网络中，并以端到端（end-to-end）的方式进行训练。

2 方法

小样本方法可以粗略地分为三种：基于non-episodic的方法、基于优化（或元学习）的方法、基于度量的方法。

当前的 FSL 方法主要关注如何 有效地从 A 中学习可迁移知识以快速适应（基于元学习方法和基于non-episodic的方法）或 在 S 上通过少量标记实例进行良好的泛化（基于度量学习的方法）。

2.1 基于non-episodic的方法

基于non-episodic的方法 通常遵循标准的迁移学习程序，包括两个阶段：使用基类进行 预训练 和使用新类进行 微调 ，如图所示：

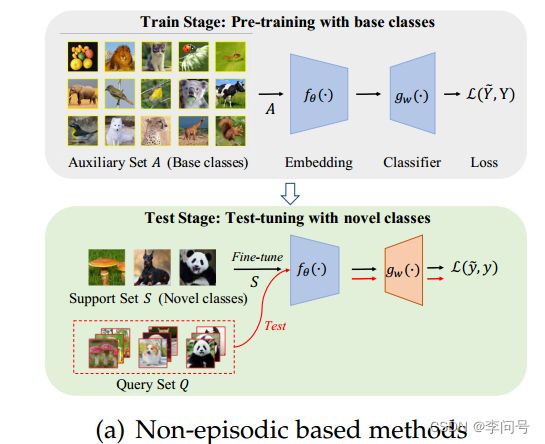
使用基类进行预训练。 在此阶段，整个辅助集 A 用于通过使用 标准交叉熵损失 来训练一个 $C_{base}$ 类的分类器，如下所示

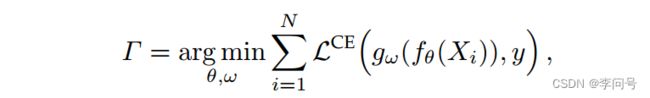
使用新类进行微调。 调整在测试阶段进行。具体来说，对于每个特定的新任务$T=⟨{\mathcal{A}}_{\mathcal{S}},{\mathcal{A}}_{\mathcal{Q}}⟩$ ，每次都会基于 S 重新学习一个新的 N 类分类器。基本上，因为 S 中的标记实例有限，预训练的嵌入参数 θ 是固定的，以避免过度拟合。这个新的 N 类分类器被学习之后，就可以用来预测 Q 中实例的标签。

代表性论文： Self-Promoted Supervision for Few-Shot Transformer (ECCV 2022)
关于该论文的详细讲解，可以看这篇文章:https://blog.csdn.net/Bluebro/article/details/129990479?spm=1001.2014.3001.5501

简单来说，在元训练阶段，为全局特征嵌入提供全局监督，并进一步采用单独的特定位置监督来指导每个patch标记，用每个patch 标记的置信度分数作为伪标签进行特定位置监督。在元微调阶段，使用现有方法（例如原型网络）在 大量few-shot任务 上微调 f（此处有些不同），使在元训练阶段学习到的 表示 适应新任务，然后使用支持集 S 预测每个查询 x 的标签。

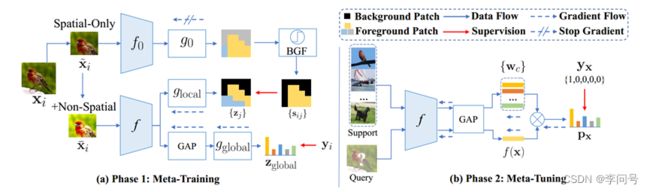
相比基于 纯元训练或episodic训练 的方法，基于non-episodic的方法以更简单的方法取得了非常不错的结果。但是，预训练阶段使用的交叉熵损失可能会使学习到的 表示 对基类数据 过拟合 ，从而缺乏对未见类的泛化能力。此外，基于non-episodic的方法严格遵循标准 迁移学习 的范式，并着重于利用最新和流行的深度学习技巧来改进预训练阶段，这可能在某种程度上 忽略了 FSL 的内在问题 。

2.2 基于优化的方法

如图所示，基于元学习的方法 在训练阶段 对从基类构建的一系列 few-shot任务 执行 元训练范式。 旨在使学习到的模型能够在测试阶段快速适应未见过的新任务。

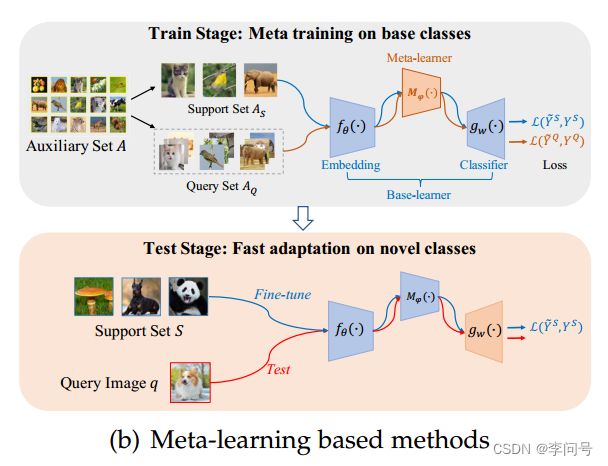
元训练过程包括 基础学习器(base-learner)和元学习器(meta-learner) 之间的两步优化。具体来说，给定一个采样任务 $T=⟨{\mathcal{A}}_{\mathcal{S}},{\mathcal{A}}_{\mathcal{Q}}⟩$
第一步（即base-learning或内循环）是使用 $A_S$（即每个任务中的训练实例）来学习基础学习器。
第二步（即元微调或外循环），使用 $A_Q$（即每个任务中的测试实例）来优化元学习器。通过这种方式，元学习者有望学习一种跨任务的元知识，可用于快速适应新任务。

代表性论文：Model-Agnostic Meta-Learning for Fast Adaptation of Deep Network(PMLR 2017)
Model-Agnostic Meta-Learning (MAML) 其核心思想是通过引入 二阶梯度 来训练模型的初始参数，使该模型只需一个或一个几个梯度步骤就能够快速适应新任务。
在base-learning阶段(内循环)，给定$T=⟨{\mathcal{A}}_{\mathcal{S}},{\mathcal{A}}_{\mathcal{Q}}⟩$，当前模型 $F_{\Theta }=f_{\theta }◦g_{\omega }，\Theta ={\Theta }_0$，我们可以得到第 m 次内循环梯度更新为：

其中 $\Theta =\theta ,\omega$， α 是步长超参数， m 是内部迭代的总数。
在元微调阶段(外循环)，模型的参数是使用查询集 $A_Q$ 根据之前的参数 $\Theta$而不是 ${\Theta }_m$ 进行更新的：

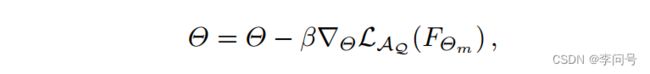
早期基于元学习的方法主要采用 纯元训练范式 从头开始学习模型，现在有很多方法将预训练引入到训练过程，值得进一步研究。

2.3 基于度量的方法

如图所示，基于度量学习的方法直接比较查询图像和支持类之间的相似性（或距离），通过 episodic-training策略 的一次单向前馈。不同于基于元学习的方法的双循环结构。

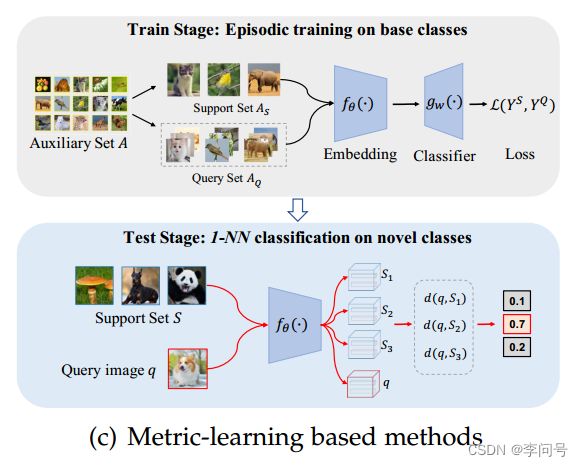
换句话说，对于每个输入的查询图像，整个支持集 $A_S$ 同时被编码到潜在嵌入空间中，并使用查询图像和支持集的关系（即输出）进行分类。通过对支持集进行调整，能够使模型适应每个任务的特征，并使学习到的 表示 在不同任务之间可迁移。

代表性论文1：Prototypical Networks for Few-shot Learning(NIPS2017)
Prototypical Networks（ProtoNet） 是一种典型的基于度量学习的方法，它将每个支持类的 均值向量 作为其对应的 原型表示 ，然后比较查询图像和原型的关系。

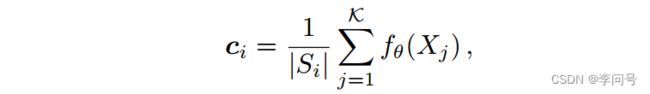
其中，$|S_i|$表示第i个支持类的实例数量，$f_{\theta }(\cdot )$ 为每个图像提取d维的 全局特征表示 。
给定距离函数 $D(\cdot ,\cdot )$，例如欧氏距离，查询图像 Q 的预测后验概率分布为:

$\rho (y=i\mid Q)=\frac{\exp \left(-D\left(f_{\theta }(Q),{\mathbf{c}}_i\right)\right)}{{\sum }_{j=1}^N\exp \left(-D\left(f_{\theta }(Q),{\mathbf{c}}_j\right)\right)}.$

在训练阶段，可以采用标准的交叉熵损失来训练整个模型。在测试阶段，可以使用最近邻分类器（1-NN）进行预测。

损失函数总结：

1. 对于常见分类(基于non-episodic的预训练阶段)和基于元学习的base-learner，损失函数表示为$\mathcal{L}\left(g_{\omega }\left(f_{\theta }(X)\right),y\right)$
2. 对于基于度量的方法，损失函数表示为$\mathcal{L}\left(g_{\omega }\left(f_{\theta }(X)\mid \mathcal{S}\right),y\right)$

代表性论文2：Revisiting Local Descriptor based Image-to-Class Measure
for Few-shot Learning(CVPR2019)
深度最近邻神经网络 (DN4) 是另一种代表性方法，它认为将局部特征池化为紧凑的全局级表示将丢失大量的判别信息。因此，DN4 提倡直接使用原始 局部特征 ，并采用基于图像到类 (image-to-class) 的局部描述符的方法来学习可迁移局部特征。

具体来说，给定输入图像 X，没有嵌入网络的最后一个池化或 FC 层，$f_{\theta }(X)\in {\mathbb{R}}^{d\times h\times w}$ 将是一个三维张量(tensor)，并且可以重塑为一组 d 维局部描述符:

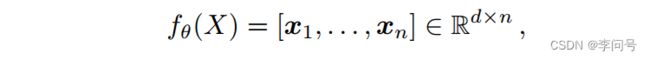
其中 $x_i$ 是第 i 个局部描述符，$n=h\times w$ 是图像 X 的局部描述符总数。

假设一个查询图像$Q$ 被表示为$f_{\theta }(Q)=\left[{\mathbf{x}}_1,\dots ,{\mathbf{x}}_n\right]\in {\mathbb{R}}^{d\times n}$
支持集S表示为：$f_{\theta }(S)=$ $\left[f_{\theta }\left(X_1\right),\dots ,f_{\theta }\left(X_K\right)\right]\in {\mathbb{R}}^{d\times nK}$
image-to-class(I2C) 方法将计算为：
$$D_{I2C}(Q,S)=\sum _{i=1}^n\mathrm{Topk}\left(\frac{f_{\theta }(Q{)}^{\top }\cdot f_{\theta }(S)}{{\Vert f_{\theta }(Q)\Vert }_F\cdot {\Vert f_{\theta }(S)\Vert }_F}\right),$$
使用余弦函数计算距离， $\Vert \cdot {\Vert }_F$ 表示 Frobenius 范数（各元素的平方和再开方，l2范数）, $\mathrm{Topk}(\cdot )$ 表示在Q和S的相关矩阵的每一行中选取k个最大的元素。

代表性论文3:Few-Shot Learning via Embedding Adaptation with Set-to-Set Functions(CVPR2020)

原型网络+Transformer