CH3-栈和队列

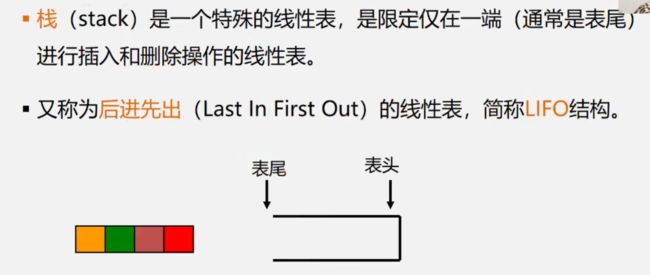
3.1栈和队列的定义和特点

• 栈和队列是两种常用的、重要的数据结构
• 栈和队列是限定插入和删除只能在表的“端点”进行的线性表

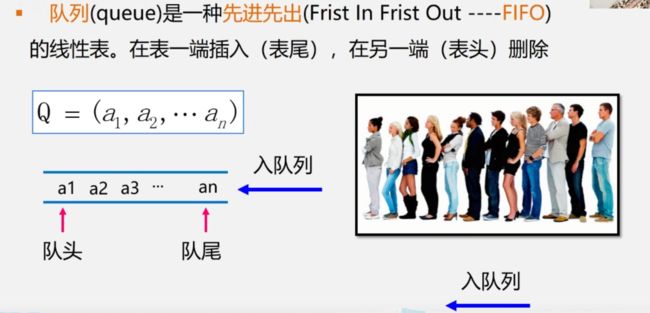
栈的应用

队列的应用

• 由于队列的操作具有先进先出的特性，使得队列成为程序设计中解决类似排队问题的有用工具。
  • 脱机打印输出，按申请的先后顺序依次输出
  • ·多用户系统中，多个用户排成队，分时地循环使用CPU和主存
  • 按用户的优先级排成多个队，每个优先级一个队列
  • 实时控制系统中，信号按接收的先后顺序依次处理
  • 网络电文传输，按到达的时间先后顺序依次进行

3.1.1栈的定义和特点

3.1.2队列的定义和特点

3.2案例引入

案例3.1 :进制转换

案例3.2:括号匹配的检验

案例3.3:表达式求值

案例3.4∶舞伴问题

3.3栈的表示和实现

3.3.1抽象数据类型定义

由于栈本身就是线性表，于是栈也有顺序存储和链式存储两种实现方式

• 栈的顺序存储—顺序栈
• ·栈的链式存储—链栈

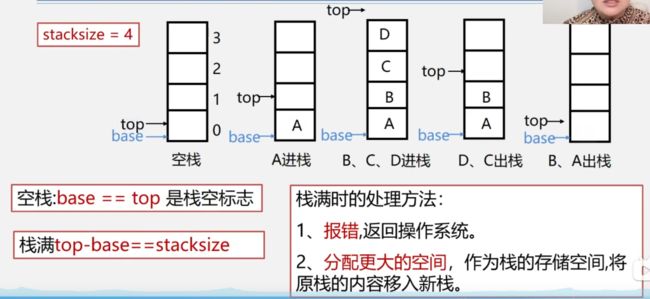
3.3.2顺序栈

使用数组作为顺序栈存储方式的特点:

​ 简单方便、但易产生溢出（数组大小固定)

• 上溢（overflow): 栈已经满，又要压入元素

  • 注:上溢是一种错误，使问题的处理无法进行;

• 下溢(underflow): 栈已经空，还要弹出元素

  • 而下溢一般认为是—种结束条件，即问题处理结束。

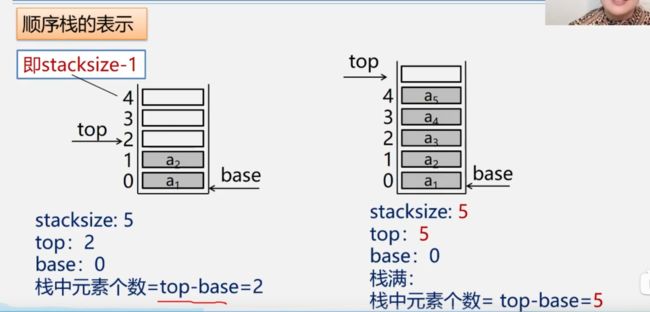
顺序栈的表示

#define MAXSIZE 100
typedef struct{
    SElemType *base;	//栈底指针
    SElemType *top;		//栈顶指针
    int stacksize;		//栈可用最大容量
}SqStack;

【算法3.1】初始化

Status InitStack(SqStack &S){//构造一个空栈
    S.base = new SElemType[MAXSIZE];
    //或S.base = (SElemType*)malloc(MAXSIZE*sizeof(SElemType));
    if (!S.base) exit (OVERFLOW);	//存储分配失败
    S.top= S.base;					//栈顶指针等于栈底指针
	S.stacksize = MAXSIZE;
	return OK;
}

【算法补充】判断栈是否为空

Status StackEmpty(SqStack S)
   // 若栈为空，返回TRUE;否则返回FALSE
    if (S.top == S.base)
    	return TRUE;
	else
    	return FALSE;
}

【算法补充】求栈长

int StackLength( SqStack S)
{
    return S.top - S.base;
}

【算法补充】清空

Status ClearStack( SqStack S ) {
    if( S.base ) 	S.top = S.base;
    return OK;	
}

【算法补充】销毁

Status DestroyStack( SqStack &S ){
    if(S.base ) {
        delete S.base ;
        S.stacksize = O;
        S.base = S.top = NULL;
    }
    return OK;
}

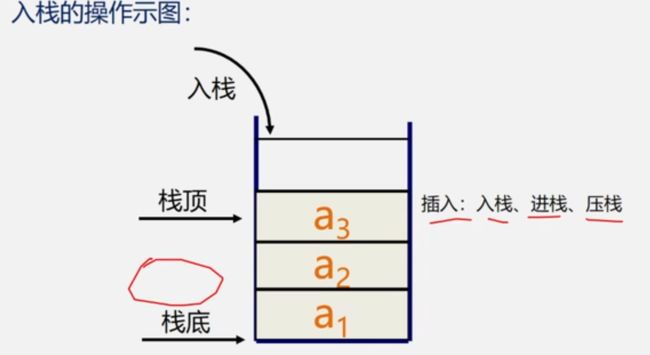
【算法3.2】入栈

• (1)判断是否栈满，若满则出错（上溢)
• (2)元素e压入栈顶
• (3)栈顶指针加1

Status Push( SqStack &S, SElemType e) {
    if( S.top - S.base== S.stacksize )//栈满
   		return ERROR;
    *S.top++=e;				//*S.top=e;	S.top++;
	return OK;
}

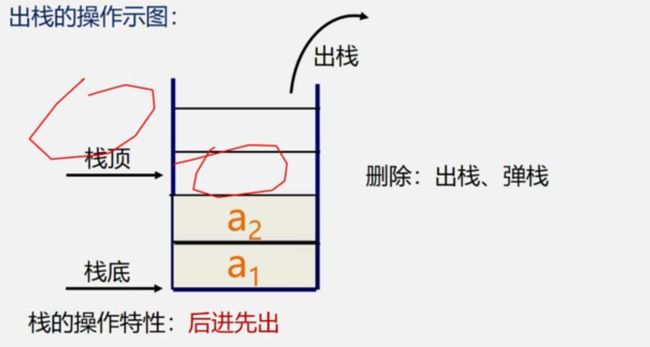
【算法3.3】出栈

• (1)判断是否栈空，若空则出错（下溢)
• (2)获取栈顶页元素
• (3)栈顶指针减1

Status Pop(SqStack &S, SElemType &e){
//若栈不空，则删除S的栈顶无素，用e返回其值，并返回OK;否则返回ERROR
    if(S.top == S.base)		//等价于if(StackEmpty(S))
        return ERROR;
    e = *--S.top;			//--S.top;	e=*S.top; 
    retum OK;
}

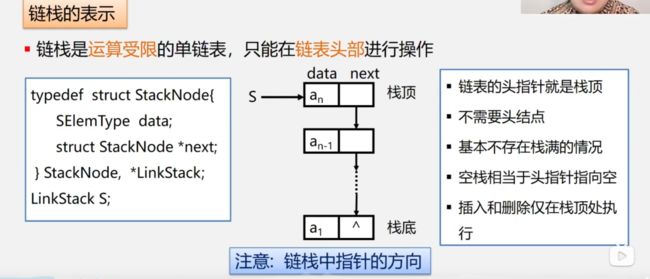
3.3.3链栈

typedef struct StackNode{
    SElemType data;
    struct StackNode *next;
} StackNode,*LinkStack;LinkStack S;

【算法3.5】初始化

void lnitStack(LinkStack &S ) {//构造一个空栈，栈顶指针置为空
	S=NULL;
	return OK;
}

【补充算法】判断栈是否为空

Status StackEmpty(LinkStack S)
    if (S==NULL) return TRUE;
    else return FALSE;
}

【算法3.7】出栈

Status Pop (LinkStack &S,SElemType &e){
    if (S==NULL)	return ERROR;
    e = S-> data;
    p = S;
    S = S-> next;
    delete p;
    return OK;
}

【算法3.8】取栈顶元素

SElemType GetTop(LinkStack S) {
    if (S!=NULL)	
    	return S->data;
}

3.4栈与递归

递归的定义

• 若一个对象部分地包含它自己 ，或用它自己给自己定义，则称这个对象是递归的;

• 若一个过程直接地或间接地调用自己,则称这个过程是递归的过程。

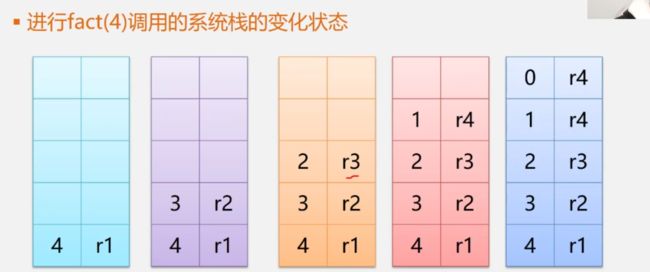
  • 例如:涕归求n的阶乘

    long Fact ( long n ) {
        if ( n == 0) 	return 1;
        else 	return n * Fact (n-1);
    }
    

• 以下三种情况常常用到递归方法

  • 递归定义的数学函数
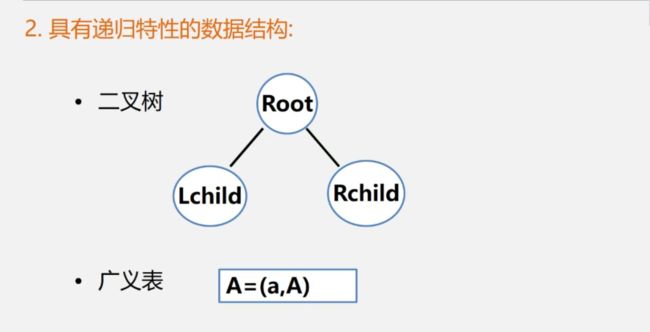
  • ·具有递归特性的数据结构
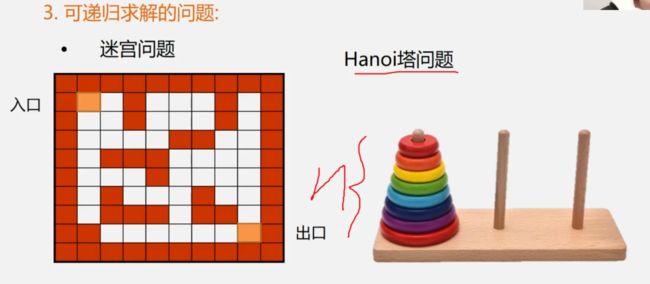
  • 可递归求解的问题

递归问题——用分治法求解

• 分治法: 对于一个较为复杂的问题，能够分解成几个相对简单的且解法相同或类似的子问题来求解
• 必备的三个条件
  • 1、能将一个问题转变成、个新问题，而新问题与原问题的解法相同或类同，不同的仅是处理的对象，且这些处理对象是变化有规律的
  • 2、可以通过上述转化而使白题简化
  • 3、必须有一个明确的递归出口，或称递归的边界

递归的优缺点

3.5队列的表示和实现

3.3.1抽象数据类型定义

3.5.2顺序队列

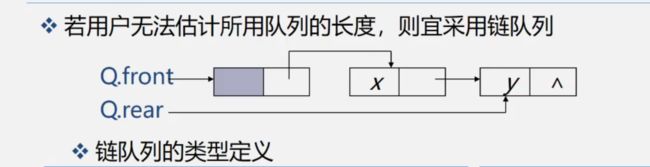
• 队列的物理存储可以用顺序存储结构，也可用链式存储结构, 队列的存储方式也分为两种，即顺序队列和链式队列。

• 队列的顺序表示——用一维数组base[MAXQSZE]

#define MAXQSIZE 100//最大队列长度
Typedef struct {
    QElemType *base;//初始化的动态分配存储空间
    int front;		//头指针
    int rear		//尾指针
}SqQueue;

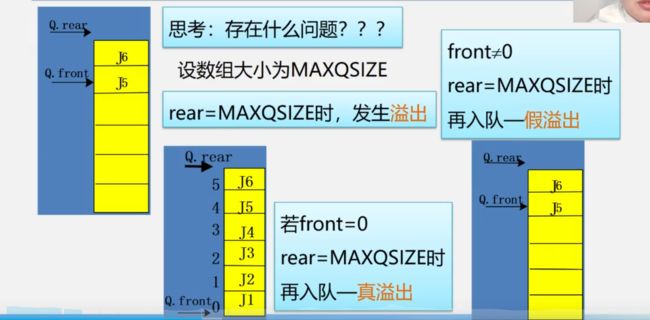
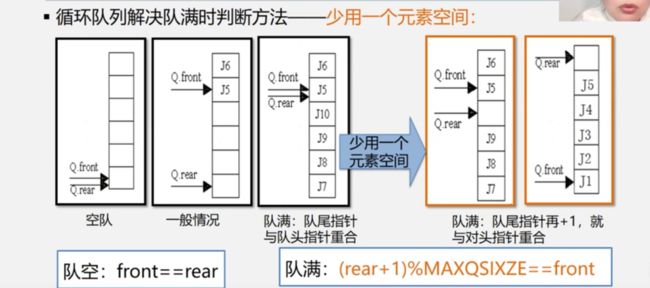
解决假上溢的方法——引入循环队列

类型定义

#define MAXQSIZE 100//最大队列长度
typedef struct {
    QElemType *base;//动态分配存储空间
    int front;		//头指针，若队列不空，指向队列头元素
    int rear;		//尾指针，若队列不空，指向队列尾元素的下一个位置
} SqQueue;

【算法3.4】初始化

Status lnitQueue (SqQueue &Q){
    Q.base =new QElemType[MAXQSIZE]		//分配数组空间
    //Qbase = (QElemType*)malloc(MAXQSIZE*sizeof(QElemType));
    if(!Q.base)exit(OVERFLOW);			//存储分配失败
    Q.front=Q.rear=O;					//头指针尾指针置为0，队列为空
    return OK;
}

【算法3.5】求队长

int QueueLength (SqQueue Q){
    return (Q.rear-Q.front+MAXQSIZE)% MAXQSIZE );
}

【算法3.6】入队

Status EnQueue(SqQueue &Q, QElemTypee){
    if((Q.rear+1)%MAXQSIZE==Q.front)	return ERROR;		//队满
    Q.base[Q.rear]=e;				//新元素加入队尾
    Q.rear=(Qrear+1)%MAXQSIZE;	    //队尾指针+1
    return OK;
}

【算法3.7】出队

Status DeQueue (SqQueue &Q,QElemType &e){
    if(Q.front==Qrear)	 return ERROR;	//队空
    Q.base[Q.front];						//保存队头元素
    Q.front=(Q.front+1)%MAXQSIZE;		//队头指针+1
    return OK;
}

【算法3.8】取队头元素

SElemType GetHead(SqQuere Q){
    if(Q.front!=Q.rear)			//队列不为空
    	return Q.base[Q.front];	//返回队头指针元素的值，队头指针不变
}

3.5.3链式队列

#define MAXQSIZE 100	//最大队列长度
typedef struct Qnode {
    QElemType data;
    struct Qnode *next;
}QNode,*QuenePtr;

typedef struct {
    QuenePtr front;//队头指针
    QuenePtr rear;//队尾指针
}LinkQueue;

【算法3.4】初始化

Status InitQueue (LinkQueue &Q){
    Q.front=Q.rear=(QueuePtr) malloc(sizeof(QNode));
    if(!Q.front) 	exit(OVERFLOW);
    Q.front->next=NULL;
    return OK;
}

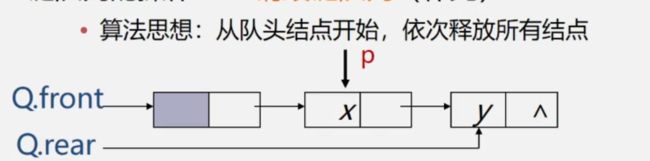
【算法补充】销毁

Status DestroyQueue (LinkQueue &Q){
    while(Q.front){
        p=Q.front->next;	//Q.rear=Q.front->next; 
        free(Q.front);		//free(Q.front);
        Q.front=p;			//Q.front=Q.rear;
    }
    return OK;
}

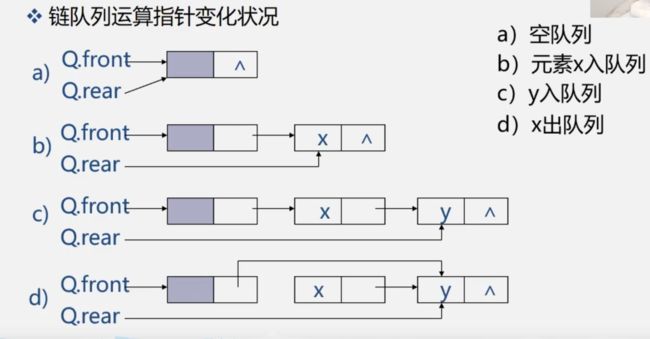
【算法3.6】入队

Status EnQueue(LinkQueue &Q, QElemType e){
    p=(QueuePtr)malloc(sizeof(QNode));
    if(!p) 	exit(OVERFLOW);
    p->data=e;	 p->next=NULL;
    Q.rear->next=p;
    Q.rear=p;
    return OK;
}

【算法3.7】出队

Status DeQueue (LinkQueue &Q,QElemType &e){
    if(Q.front==Q.rear)		 return ERROR;
    p=Q.front->next;
    e=p->data;
    Q.front->next = p->next;
    if(Q.rear==p)	Q.rear=Q.front;	
    delete p;
    return OK;
}

【算法3.8】取队头元素

Status GetHead (LinkQueue Q, QElemType &e){
    if(Q.front==Q.rear) 	return ERROR;
	e=Q.front->next->data;
	return OK;
}

ueue &Q, QElemType e){
p=(QueuePtr)malloc(sizeof(QNode));
if(!p) exit(OVERFLOW);
p->data=e; p->next=NULL;
Q.rear->next=p;
Q.rear=p;
return OK;
}

### 【算法3.7】出队

[外链图片转存中...(img-QNfcYgtG-1641895287115)]

```c
Status DeQueue (LinkQueue &Q,QElemType &e){
    if(Q.front==Q.rear)		 return ERROR;
    p=Q.front->next;
    e=p->data;
    Q.front->next = p->next;
    if(Q.rear==p)	Q.rear=Q.front;	
    delete p;
    return OK;
}

【算法3.8】取队头元素

Status GetHead (LinkQueue Q, QElemType &e){
    if(Q.front==Q.rear) 	return ERROR;
	e=Q.front->next->data;
	return OK;
}