算法的时间复杂度和空间复杂度(1)

1.算法效率
2.时间复杂度
3.空间复杂度

1.算法效率
如何衡量一个算法的好坏？
比如对于以下斐波那契数列：

long long Fib(int N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2)；
}

斐波那契数列的递归实现方式非常简洁，但简洁一定好吗？那该如何衡量其好与坏呢？
 

算法的复杂度
算法在编写成可执行程序后，运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏，一般是从时间和空间两个维度来衡量的，即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢，而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展，计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。

复杂度在校招中的考察
在校园招聘的笔试算法题和面试中都会考察对复杂度的计算和理解。

2.时间复杂度
时间复杂度的概念
时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。一个算法执行所耗费的时间，从理论上说，是不能算出来的，只有你把你的程序放在机器上跑起来，才能知道。但是我们需要每个算法都上机测试吗？是可以都上机测试，但是这很麻烦，所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。
即：找到某条基本语句与问题规模N之间的数学表达式，就是算出了该算法的时间复杂度。

请计算一下Func1中++count语句总共执行了多少次？
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
 {
for (int j = 0; j < N ; ++ j)
 {
           ++count;
 }
 }
for (int k = 0; k < 2 * N ; ++ k)
 {
++count;
 }
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}

Func1 执行的基本操作次数：F(N)=N*N+2*N+10

假设N = 10 准确值:F(N) = 130  估算值:100
假设N = 100 准确值:F(N) = 10210 估算值:10000
假设N = 1000 准确值:F(N) = 1002010 估算值:1000000

N越大，后面项对结果影响越小。

所以func1的时间复杂度为O(N^2)

实际中我们计算时间复杂度时，我们其实并不一定要计算精确的执行次数，而只需要大概执行次数，那么这里我们使用大O的渐进表示法。
 

计算Func3的时间复杂度？
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++ k)
{
++count;
}
for (int k = 0; k < N ; ++ k)
{
++count;
}
printf("%d\n", count);
}

因为不确定M和N的对应的值，所以不能够确定M和N对各自的效果是不是微乎其微，书面来说是同阶的数，所以不能忽略N或M，应该是N+M。 

Fucn3的时间复杂度为O(N+M) 

计算Func4的时间复杂度？
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++ k)
{
++count;
}
printf("%d\n", count);
}

Func4的时间复杂度为O(1)

因为1表示的不是数字1，而是代表常数次，因为 k<100,是一个常数。

 无论常数数字多大，都是很快运行出来，是因为跟计算机的cpu有关，现在计算机的cpu计算速度太快，因为我们日常生活需要的值都不超亿或者最大也就亿，在cpu面前没有区别，因为现在cpu的计算速度太快，所有常数对于cpu看起来都一样，就跟有钱人去酒吧喝酒，说今晚的消费我买单！你心里很开心，去消费了一万，暗自窃喜，这对于你很贵，但对于有钱人这种小钱微乎其微，有钱人也知道我们普通人的消费水平，所以cpu相当于千万富翁，我们眼中的大数字钱，不过是人家的零花钱罢了，所以，所有常数的时间复杂度在cpu面前就为O(1)。

大O的渐进表示法
大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。
推导大O阶方法：
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中，只保留最高阶项。
3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后，Func1的时间复杂度为O(N^2)

计算Func2的时间复杂度？
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);

Func2 时间复杂度为O(2*N)?NO!是O(N)，当N无限大，2可以被忽略。

通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项，简洁明了的表示出了执行次数。
 

计算strchr的时间复杂度？
const char * strchr ( const char * str, int character );

strchr相当于 

另外有些算法的时间复杂度存在最好、平均和最坏情况：
最坏情况：任意输入规模的最大运行次数(上界)
平均情况：任意输入规模的期望运行次数
最好情况：任意输入规模的最小运行次数(下界)
例如：在一个长度为N数组中搜索一个数据x
最好情况：1次找到
最坏情况：N次找到
平均情况：N/2次找到
在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N)。

算法的最坏:降低预期，底线思维。

计算BubbleSort的时间复杂度？冒泡排序
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}

BubbleSort的时间复杂度为O(N^2)

因为有N个元素，第一次比较N-1，第二次N-2，第三次N-3.....3 2 1....相当于等差数列，N*(N*-1)/2。 

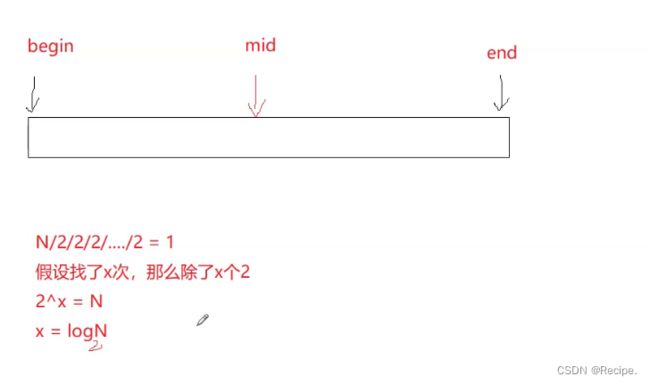
计算BinarySearch的时间复杂度？ 二分查找
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n-1;
[begin, end]：begin和end是左闭右闭区间，因此有=号
while (begin <= end)
{
int mid = begin + ((end-begin)>>1);
if (a[mid] < x)
begin = mid+1;
else if (a[mid] > x)
end = mid-1;
else
return mid;
}
return -1;
}

BinarySearch的时间复杂度O(logN)

有N个元素，每次折半查找N/2/2/2，假设找了X次

2^30= 1073741824

如果我们在中国查找某个人的信息要查找多少次？是31次，因为30次已经10亿多一点，中国有14亿人口，2^31。

 

计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N)
{
if(0 == N)
return 1;
return Fac(N-1)*N;
}

阶乘递归Fac的时间复杂度 O(N)   fac()递归了N次,*N可以看做常数。