11.深度优先搜索

一、算法内容

1.简介

深度优先搜索DFS（Depth First Search）按照深度优先的方式进行搜索，可以理解为“一条路走到黑”地穷举所有可行的方案，并不断尝试，直到找到一种情况满足问题问题的要求。那么这个方案就是一个问题的解。

2.递归与回溯

深度优先搜索可以用递归实现，而且几乎都是用递归实现，所以要学会深度优先搜索，首先必须要学会递归。但切忌将递归与深度优先搜索混为一谈。深度优先搜索和递归的区别是：深度优先搜索是一种算法，注重的是思想；而递归是一种基于编程语言的实现方式。

深度优先搜索最重要地就是回溯，它的作用是将状态恢复到上一级。你可以想象小时候玩迷宫游戏的行为，选择某一些路径进行尝试，如果不行就倒回来走其他的地方，这样倒回去的操作就是回溯。只有不断地尝试，不断地回溯才是一个完整的深度优先搜索。

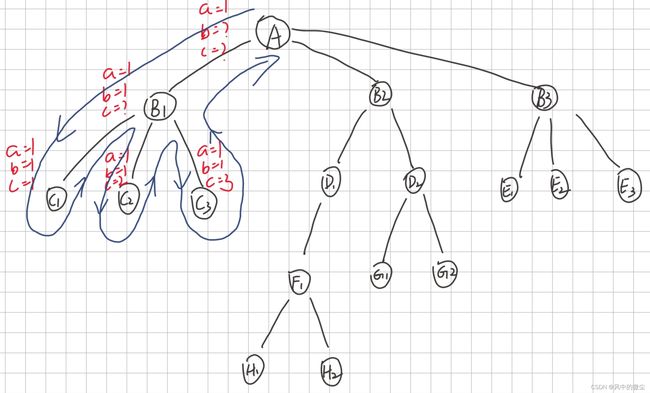
如果将搜索的过程画出来，那么它就像一棵树，每一个结点都有相应的状态，分别代表了一种可能性。之所以叫做深度优先，是因为我们总是走到树的叶子处才开始返回，在树上就是先往深的地方走。

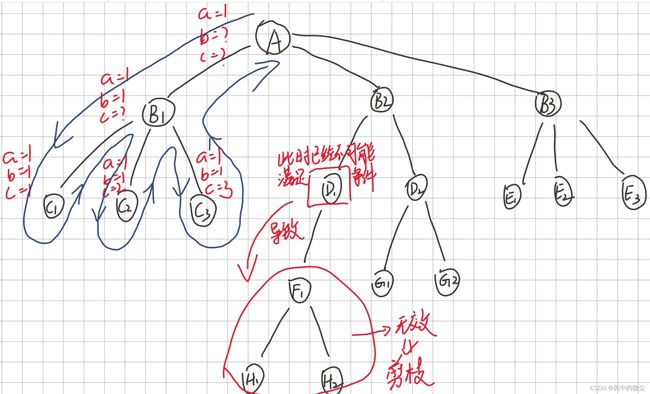
3.剪枝

在我们搜索的时候，理论上我们需要把所有的情况都考虑到，但是实际上，有一些情况我们不需要走到尽头就知道这是不合理的。就像走到树上的某一个位置之后，我们知道接下来无论走到哪里都不可能得到正确的答案了，那么就可以直接返回，相当于剪掉了搜索树上的一根树枝。

剪枝是搜索的精髓所在，如何更好地找到剪枝的策略会极大影响程序的时间复杂度。剪枝一般分为以下三种：

• 可行性剪枝：如果按照这样的方案继续下去，不可能满足题目条件，那么剪枝。
• 最优性剪枝：如果按照这样的方案继续下去，不可能比当前答案更有，那么剪枝。
• 重复性剪枝：如果按照这样的方案继续下去，与此前某些时候相同，那么剪枝。

二、算法实现

1.算法模板

参数 dfs(变量)
{
    判断终点:
    	检查答案;
        返回;
    剪枝1:
    	返回;
    剪枝2:
    	返回;
    ...
    枚举:
    	条件检测:
            更新状态1;
            更新状态2;
            ...
            dfs();
            恢复状态1;
            恢复状态2;
    	...
}

2.实例剖析：P1605 迷宫

（1）限定条件

• 不能走出迷宫，即任何时候，当前坐标$(x,y)$满足$1\le x\le n,1\le y\le m$。
• 当走到终点的时候记录一次答案，并停止该分支。
• 不能走到障碍物上面。
• 注意不要原路返回，否则将进入无限循环。

（2）更新状态

若当前坐标为$(x,y)$，则下一步的坐标即为$(x-1,y),(x+1,y),(x,y-1),(x,y+1)$。我们需要在限定条件内走到这些位置。

而我们的状态分为两部分构成，结合这两个状态我们就可以唯一标识一种情况：

• 第一部分：显然我们当前的坐标是我们的一个状态。
• 第二部分：为了保证我们不要进入循环，我们需要标记我们的来路，这就是第二部分的状态。

（3）正解代码

#include 
#include 
#include 
#include 
#include  
#include 

using namespace std;
typedef long long ll;
ll dx[4]={0,0,1,-1},dy[4]={-1,1,0,0};
ll mp[10][10];
ll ans,t,n,m;
ll fx,fy,sx,sy;
void dfs(ll x,ll y)
{
    if(x==fx && y==fy)
    {
        ans++;
        return;
    }
    else
    {
        for(ll i=0;i<4;i++)
        {
        	ll tx=x+dx[i];
        	ll ty=y+dy[i];
            if(tx>=1 && tx<=n && ty>=1 && ty<=m && mp[tx][ty]==0)
            {
            	mp[tx][ty]=1;
                dfs(tx,ty);
                mp[tx][ty]=0;
            }
        } 
    }
}
int main()
{
    cin>>n>>m>>t;
    cin>>sx>>sy>>fx>>fy;
    for(ll i=1;i<=t;i++)
    {
    	ll x,y;
        cin>>x>>y;
        mp[x][y]=1;
    }
    mp[sx][sy]=1;
    dfs(sx,sy);
    cout<<ans<<endl;
    
    return 0;
} 

三、作业

1.橙题

P1010 [NOIP1998 普及组] 幂次方

P1036 [NOIP2002 普及组] 选数

P1162 填涂颜色

P1605 迷宫

2.黄题

P1019 [NOIP2000 提高组] 单词接龙

P1219 [USACO1.5]八皇后 Checker Challenge

P1259 黑白棋子的移动

P1434 [SHOI2002] 滑雪

P1443 马的遍历