基本思想
每趟不断记录两两比较,如果发生逆序则按"前小后大"规则交换,直到所有记录都排好序为止;
常见的交换排序方法
- 冒泡排序(O(n²)) ------ 稳定
- 快速排序(O(nlog2n))
冒泡排序 ------ 基于简单交换思想(稳定)
初始: 21, 25, 49, 25*, 18, 08 n=6
第一趟: 位置0,1进行比较-判断-不交换,结果:
21, 25, 49, 25*, 18, 08
位置1,2进行比较-判断-不交换,结果:
21, 25, 49, 25*, 18, 08
位置2,3进行比较-判断-交换,结果:
21, 25, 25*, 49, 18, 08
位置2,3进行比较-判断-交换,结果:
21, 25, 25*, 18, 49, 08
位置2,3进行比较-判断-交换,结果:
21, 25, 25*, 18, 08, 49
第一趟结束,序列中的49元素被移动到了序列末位;
继续下一趟,每一趟增加一个有序元素;
第二趟结束:
21, 25, 18, 08, 25*, 49
...直到第五趟:
08, 18, 21, 25, 25*, 49
总结: n个记录,总共需要 n-1 趟;
每一趟需要比较n-m次(m为趟数);
void bubble_sort(SqList &L) {
int m,i,j;
int flag = 1;
RedType x;
n = L.length
for (m = 1; m <= n-1 && flag == 1; m++) {
flag = 0;
for (j = 1; j <= n-m; j++)
if (L.r[j].key > L.r[j+1].key) {
flag = 1;
x = L.r[j];
L.r[j] = L.r[j+1];
L.r[j+1] = x;
}
}
}
冒泡排序优劣
优点: 每趟结束时,不仅能挤出一个最大值到最后面位置,还能同时部分理顺其他元素;
如何提高效率?
一旦某一趟比较时不出现记录交换,说明已经排好序了,就可以结束本算法.
冒泡排序算法分析
时间复杂度:
最好情况:(正序)
比较次数: n-1次
移动次数:0次
最坏情况:(逆序)
比较次数: (n-1)+(n-2)+..+0 = (n²-n)/2
移动次数: 两个值交换,存在一个中间变量,则有3(n²-n)/2
冒泡排序最好时间复杂度为O(n);
冒泡排序最坏时间复杂度为O(n²);
冒泡排序平均时间复杂度为O(n²);
冒泡排序算法中增加一个辅助空间temp,复制空间为S(n)=O(1);
冒泡排序是稳定的;
快速排序 ------ 改进的交换排序(不稳定)
基本思想:
任取一个元素(如: 第一个)为中心: pivot: 枢轴,中心点;
所有比它小的元素一律前放,比它大的元素一律后放,形成左右两个子表;
对各子表重新选择中心元素并依此规则调整; ------ 递归思想-
直到每个子表的元素只剩一个;
通过一趟排序,将待排序记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录进行排序,以达到整个序列有序.
具体实现: 选定一个中间数作为参考,所有元素与之比较,小的调到其左边,大的调到其右边.
(枢轴)中间数: 可以是第一个数,最后一个数,最中间的数,任选一个数等.
初始:下标为0的哨兵位置不放数据,low指向第一个元素,high指向最后一个元素;
将序列的第一个元素选为界点放入哨兵位置,此时low指向为空,high与界点比较
若high大,则high向左移动;
若high小,则将high指向的元素换到low指向的位置,然后low向右移动;
直到low与high在序列的某个位置相遇,则找到了界点放置的位置,此时将哨兵位置的元素放置到这里.
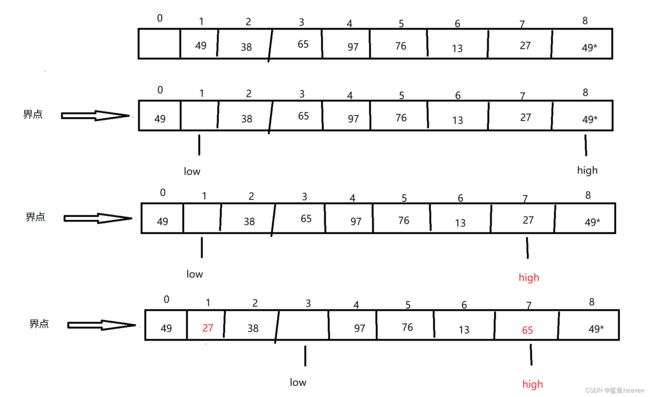
快速排序算法
- 每一趟的子表的形成是采用从两头向中间交替式逼近法;
- 由于每趟中对各子表的操作都相似,可采用递归算法;
void QSort(SqList &L, int low, int high) {
if (low < high) {
pivotloc = Partition(L, low, high);
QSort(L, low, pivotloc-1);
QSort(L, pivotloc+1, high);
}
}
int Partition(SqList &L, int low, int high) {
L.r[0] = L.r[low];
pivotloc = L.r[low].key;
while (low < high) {
while (low < high && L.r[high].key >= pivotloc) --high;
L.r[low] = L.r[high];
while (low < high && L.r[low].key <= pivotloc) ++low;
L.r[high] = L.r[low];
}
L.r[low] = L.r[0];
return low;
}
快速排序算法分析(不稳定)
时间复杂度:
可以证明,平均计算时间是O(nlogn);
就平均计算时间而言,快速排序是我们所讨论的所有内排序方法中最好的一个;
空间复杂度:
快速排序不是原地排序;
由于程序中使用了递归,需要递归调用栈,而栈的长度取决于递归调用的深度.
在平均情况下: 需要O(logn)的栈空间;
最坏情况下: 栈空间可达O(n);
稳定性:
快速排序是一种不稳定的排序方法;
对于原本有序的或基本有序的记录进行排序,由于每次枢轴记录的关键字都是大于其它所有记录的关键字,致使依次划分之后得到的子序列(1)的长度为0,这时已经退化成为没有改进措施的冒泡排序;
故快速排序不适用于对原本有序或基本有序的记录序列进行排序;
划分元素的选取是影响时间性能的关键;
输入数据次序越乱,所选划分元素值的随机性越好,排序速度越快,快速排序不是自然排序方法;
