CS188-Project 4-2
CS188-Project 4
- Eliminate
-
- 题目简述
- 游戏过程
- 代码实现
- 结果展示
- Normalize
-
- 题目简述
- 游戏过程
- 代码实现
- 结果展示
- Variable Elimination
-
- 题目简述
- 游戏过程
- 代码实现
- 结果展示
- 收获
Eliminate
题目简述
变量消元方法是用于降低贝叶斯网推理复杂度的主要手段。而变量消元的复杂度又与变量消元的顺序有关,通过一些启发式算法,可以找到较好的消元顺序。
贝叶斯网推理主要包含三大类问题:后验概率问题、最大后验假设问题和最大可能解释问题。其中后验概率问题是最基本的问题。
(1)后验概率问题
后验概率问题是指已知贝叶斯网中某些变量的值,计算另外一些变量的后验概率分布。如第一部分所使用的Alarm案例中,若接到Mary电话通知警铃响了,这时会计算『发生了盗窃』的概率是多少,即计算P(B = y|M = y)。
此类问题中,已知变量称为证据变量,记为E,取值记为e;需要计算后验概率分布的变量称为查询变量,记为Q;需要计算的后验概率分布为P(Q|E=e)。
(2)最大后验假设问题
已知证据E=e,有时会对一些变量的后验概率最大的状态组合感兴趣,这些变量称为假设变量,记作H。H的一个状态组合称为一个假设,记为h。在所有可能的假设中,找出后验概率最大的那个假设h*。MAP问题的基础是后验概率问题。但MAP问题的复杂度与假设变量H的个数呈指数关系,对实际情况,需要作特殊的化简处理。
(3)最大可能解释问题
在贝叶斯网中,证据E=e的一个解释指的是网络中全部变量的一个与E=e相一致状态组合。往往有时最关心概率最大的那个解释,即最大可能解释,简称MPE(Most probable explanation)。MPE问题可视为MAP问题的一个特例,即MAP中的假设变量H包含了网络中所有非证据变量。
而变量消元法则是贝叶斯网推理算法,变量消除法的思想就是对联合概率不断求和消除其中的变量,最后得到边缘分布。
对于给定的联合分布函数P(A,B,C,D,E),如果想要知道P(E),只需要将A,B,C,D边际掉。假设P(E)可以有两种取值P(e1),P(e2),P(e1) = P(a1,b1,c1,d1,e1)+P(a2,b1,c1,d1,e1)…以此类推,最终可以得到P(e1)与P(e2)的值。在有概率图的情况下,我们可以对变量进行因式分解,因式分解有助于减少求和的次数。
如下图所示,首先对联合概率来说,先把b消元,得到中间只含a和c的表,然后对c进行求和,得到最后只含有a的概率表,对这个表进行归一化之后,就得到了a的概率。

在贝叶斯网络中,可以通过以下贝叶斯网络写出他的因子乘积形式:
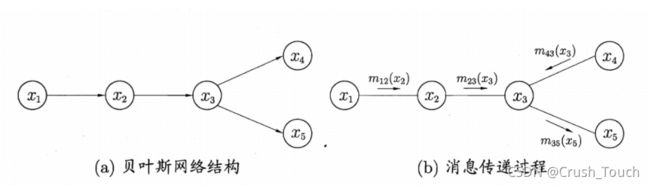

接下来要选定消元顺序为x1,x2,x4,x3
首先对x1进行消元,消元过程如下:
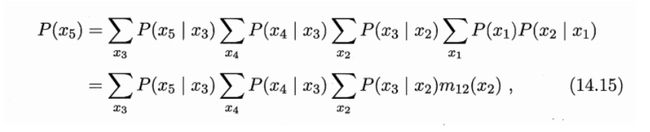
因为 p ( x 1 ) p(x_1) p(x1)和 p ( x 2 ∣ x 1 ) p(x_2|x_1) p(x2∣x1)只和x1,x2有关系,所以关于x1积分,剩下的就是关于x2的式子。将上述过程有符号表达为 m 12 ( x 2 ) m_{12}(x_2) m12(x2),其中m的第一个下标表示对那一个变量进行求和,第二个下标表示的是求和剩下的变量,其中括号内的x2,表示的是关于x2的函数。这个符号只是为了说明这一个例子,如果上面的例子复杂一点,这套符号系统就不能很好的描述问题了,实际上变量消元法有更一般化的表达方法,这里为了说明变量消元的思想,就采用这种简单的符号表达。
游戏过程
在q4中需要我们解决变量消除算法中的消除运算,要求输入一个函数集合factor(F)和待消元变量eliminationVariable(E),然后输出另一个函数集合retFactor。
q4的步骤为:(1)从F中删除所有涉及的函数E,设这些函数为{f1,f2,…,fk}。(2)将这k个函数连乘赋给g(3)对g中的E累加消元赋给h(4)将h放回F中(5)最后返回新的F即retFactor
在代码编写中,首先需要从原始因子序列中获取无条件以及条件变量。可以利用提示中提到的factor.unconditionedVariables()以及factor.conditionedVariables()来完成这一操作。其次应该利用variableDomainsDict()来获得变量的值域。
接着利用retFactor.getAllPossibleAssignmentDicts()函数来获得所有可能的概率列表,通过一个for循环来计算概率。最后返回一个新概率值。
代码实现
"*** YOUR CODE HERE ***"
# marker
# Get the unconditioned/conditioned variables from the original factor
unconditioned_variables = list(factor.unconditionedVariables())
conditioned_variables = list(factor.conditionedVariables())
variablesDomainDict = factor.variableDomainsDict()
# print("elimination_variable:", eliminationVariable)
# print("unconditioned_variables:", factor.unconditionedVariables())
# print("conditioned_variables:", factor.conditionedVariables())
# Generate our new factor
retFactor = Factor([i for i in unconditioned_variables if i != eliminationVariable], \
conditioned_variables, variablesDomainDict)
# print("retfactor:", retFactor)
# Getting and calculating the probabilities
assignments = retFactor.getAllPossibleAssignmentDicts()
print("assignments:", assignments)
print("variablesDomainDict:", variablesDomainDict)
print("eliminationVariable:", eliminationVariable)
print("eliminated_values:", variablesDomainDict[eliminationVariable])
print("variablesDomainDict[eliminationVariable]:", variablesDomainDict[eliminationVariable])
for assignment in assignments:
probability = 0
for eliminated_values in variablesDomainDict[eliminationVariable]:
prev_assignment = assignment.copy()
prev_assignment[eliminationVariable] = eliminated_values
probability += factor.getProbability(prev_assignment)
retFactor.setProbability(assignment, probability)
return retFactor
# print("==============[I MADE IT HERE]==============\n")
"*** END YOUR CODE HERE ***"
结果展示
Normalize
题目简述
机器学习中防止过拟合的方法有3种:增加数据集;正则化(多用L2正则化);Dropout(深度学习中常采用的一种正则化方法)。正则化则是通过修改损失函数防止过拟合。
P(A∣B):后验概率P(x∣D,α,β, M )
P(B|A):已知A发生的条件下,B发生的概率P(D∣x,β,M) P(A):先验概率P(x|α,M)
P(B):B的边缘概率(正则化中用作归一化因子)P(D∣α,β,M)
第一层贝叶斯框架

x:包含网络所有权值和偏置值的向量
D:训练数据集
α 与β :与密度函数相关的参数
M :代表了所选取的 网络结构,即模型
P(D∣x,β,M):已知前一次训练所得的权值x ,参数β,网络模型M的情况下,训练数据D的概率密度。
P (x|α,M):该项为模型中的先验项,即正则项,表征了权值x 的概率密度。而前一次训练所获得的权值x是在已知网络模型M 和参数α 的前提下获得的。
正则化表示对某一问题加以先验的限制或约束,以达到某种特定目的的一种手段或操作
这里的正则项可以是L1范数或L2范数
L1范数相当于加入了一个Laplacean先验项,可以保证模型的稀疏性,即某些参数等于0。
L2范数相当于加入了一个Gaussian先验项,可以保证模型的稠密性,即参数的值不会太大或者太小,比较集中。
P(D∣α,β,M):训练数据D的边缘概率,被称为证据,是个归一化因子。该项与x无关,故在最大化后验概率P(x∣D,α,β,M)时并不关心P(D∣α,β,M),但是P(D∣α,β,M)在估计参数α,β时扮演了很重要的角色。

该项可称作似然函数,是一个关于网络权值x的函数,表述了当网络权值x为什么样的组合时,训练数据D的概率密度P(D∣x,β,M)可以最大。为了获得使得P(D∣x,β,M)最大的网络权值x,在这里提出最大似然法则。若这个似然函数为一个高斯函数时,当 E D E_D ED取得最小值时,P(D∣x,β,M)取得最大值。因此可以假设训练集D含有高斯噪声,这样可以使用统计学的方法(极大似然估计)推出标准的误差平方和性能指标。
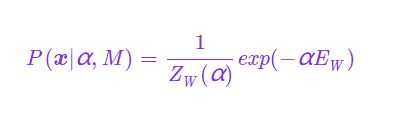
该项称为先验密度,是一个正则项,体现了在收集数据前我们对网络权值x 的了解。
贝叶斯正则化即要对该问题加以先验的限制或约束,以达到我们需要的目的的一种手段或操作。
这里的正则项可以是L1范数或L2范数:
L1范数相当于加入了一个Laplacean先验项,可以保证模型的稀疏性,即某些参数等于0。
L2范数相当于加入了一个Gaussian先验项,可以保证模型的稠密性,即参数的值不会太大或者太小,比较集中。
此处我们假设权值是以0为中心的较小值,因此选择了一个零均值的高斯先验密度。
P(D∣α,β,M)是一个归一化项,与x 无关,用来估计参数α,β。
综上,可以将第一层贝叶斯框架写成如下的形式:
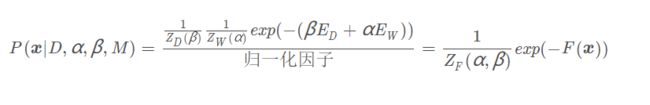
其中,F(x)=β E D E_D ED + α E W E_W EW, Z F Z_F ZF(α,β) = Z D Z_D ZD( β ) Z W Z_W ZW( α )是关于α和β的函数(与x无关)
为求权值最可能的取值,需要最大化后验密度P(x∣D,α,β,M)。这相当于最小化正则性指标F(x) = β E D E_D ED+ α E W E_W EW
游戏过程
在q5中,需要保证在贝叶斯网络中输入的概率和为1,如果输入的概率总和不为1,则直接返回。贝叶斯正则化后并不会影响最终的概率分布,因为概率分布之和必须等于1,和正则化的要求一致。同时正则化这一功能用于概率推理查询的。
q5步骤:(1)首先利用factor.getAllPossibleAssignmentDicts()函数来获得当前的概率列表;(2)计算概率的总和,如果总和不等于0,则直接返回None;(3)接着对于重复的概率,如果它不在条件概率中但在非条件概率中,则需要将挪至条件概率中,并从非条件概率中移除。(4)最后利用setProbability函数获得正则化后的新概率。
代码实现
# get list of current probabilities
probabilities = [factor.getProbability(i) for i in factor.getAllPossibleAssignmentDicts()]
uncondVars = set()
condVars = set()
varDict = {}
scaleFactor = sum(probabilities)
uncondVars.update(factor.unconditionedVariables())
condVars.update(factor.conditionedVariables())
varDict.update(factor.variableDomainsDict())
# quick check if probabilities == 0 return None don't want to divide by zero
if scaleFactor == 0:
return None
# tuples (var, domain)
for i in factor.variableDomainsDict().items():
# if domain of var is exactly 1 entry
if len(i[1]) == 1:
if i[0] not in condVars and i[0] in uncondVars:
# print("condVars: ", condVars)
# print("uncondVars: ", uncondVars)
# move to conditioned and remove from unconditioned, can't have repeat variables
condVars.add(i[0])
uncondVars.discard(i[0])
newFactor = Factor(uncondVars, condVars, varDict)
for i in newFactor.getAllPossibleAssignmentDicts():
newFactor.setProbability(i, factor.getProbability(i) / scaleFactor)
return newFactor
结果展示
Variable Elimination
题目简述
变量消除法引入原因:
假设{a,b,c,d}均是离散的二值变量,{a,b,c,d} ∈{0,1},求概率p(d)


为了求得p(d),最粗暴的一种解法便是穷举变量a,b,c,d的每一种可能性,即从:
一直穷举到:
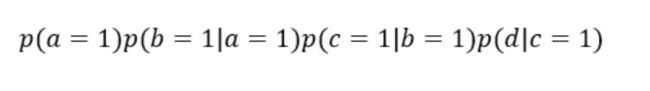
然后将8种可能性相加,便得到了最终p(d)的值,但这样显然计算过于复杂,而变量消除法的思想便是对联合概率不断求和消除其中的变量,最后得到边缘分布。下面公式展现了消除变量法的求解p(d)的过程,并依次按照变量a,b,c的顺序进行消除:
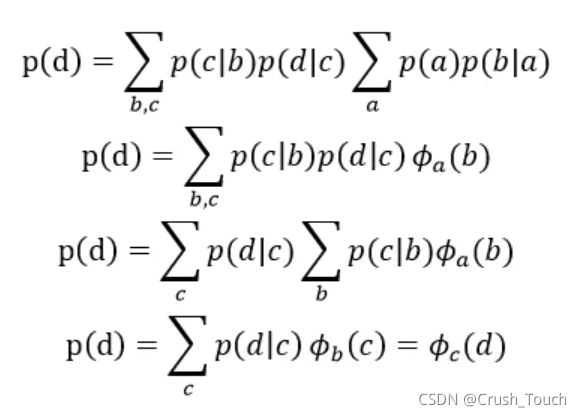
因此,可以假设对于一个无向链A-B-C-D-E,我们有如下变量消除法则:

当需要消除变量B时需包含 φ(B,C)与 τ1(B),并最后定义累加结果为 τ2©,视为与自变量为 C的函数,依次类推。
对于有向的贝叶斯网络来说,每个节点联合其父节点为一个因子,当对某一变量进行消除时,把与该变量有关的因子放到对应的连加符号右边,其他的变量与连加符号放到该连加符号左边。将所需消除的连加符号以及连加符号右边的式子,写成以右边因子中所存在的所有变量为自变量的函数ττ。
注意,该步骤之后所有因式的辖域中均不存在被消除的变量。
先对于给定的证据变量进行如上图所示的因式缩减,然后根据上文的方法进行变量消除。最后归一化。
总结:变量消除算法步骤如下
(1)根据所有的证据进行因式缩减(reduce)
(2)对于需要消除的变量 Z,把所有含有Z的变量放到 ZZ的连加右边,并连同连加符号换成一个因式τ。
(3)把得到的τ和剩下的因式乘起来。
(4)重新归一化得到分布。
游戏过程
q6要求我们需要进行变量消除来计算后验概率分布。在这过程中需要考虑概率P的所有相关因素,同时还要考虑所有因素的顺序,仅消除其中不同的变量值,最终利用消除来将概率表的变量边缘化。
q6的输入一个贝叶斯网bayesNet(N)、查询变量queryVariables(Q)、证据变量的取值evidenceDict(e)、消元顺序eliminationOrder,包含所有不在Q和E中的变量(p)证据变量(E)。要求输出 P(queryVariables | evidenceDict)
q6的步骤为:(1)将N中所有概率分布的集合赋值给F(2)在F的因子中,将证据变量E设置为其观测值e(3) 如果p不为空,设Z为p中排在最前面的变量,将Z从p中删除。然后利用q4的Eliminate函数进行消元(4)将F中所有因子相乘,得到Q的函数h(Q)(5)最后利用q5完成的normalize函数重新归一化得到分布。最后返回概率 P(Q|E=e)
代码实现
"*** YOUR CODE HERE ***"
tables = bayesNet.getAllCPTsWithEvidence(evidenceDict)
# print(tables)
# eliminate in order
for i in eliminationOrder:
# perform inference by interleaving joining on a variable and eliminating that variable
# (factors not joined, resulting factor from joinFactors)
joinTuple = joinFactorsByVariable(tables, i)
# print(joinTuple[0])
tables = joinTuple[0]
# If a factor to eliminate a variable from has only one unconditioned variable,
# you should not eliminate it and instead just discard the factor.
if len(joinTuple[1].unconditionedVariables()) == 1:
continue
tables.append(eliminate(joinTuple[1], i))
newFactor = joinFactors(tables)
return normalize(newFactor)
# util.raiseNotDefined()
"*** END YOUR CODE HERE ***"
结果展示
收获
一、本次实习主要是期望我们完成贝叶斯网的变量消元法,与前面几小题相同,题目之间也具有递进关系。这次实习通过3个小问来帮助我们实现这一过程。首先通过q4来帮助我们完成消元操作,其次通过q5来帮助我们完成归一化操作,最后通过q6来调用q4,q5使用的函数来完成变量消元法。
二、变量消元法的目的就是去除枚举法中的重复计算。VE变量消元法整体过程为(1)确定消元顺序(2)然根据后贝叶斯网给出的联合分布的分解(3)VE算法首先设置证据F=0(4)依照消元顺序p,依次消去变量(5)最后重新归一化得到分布
而在本次实习中,步骤2,3由q6完成;步骤1,4由q4完成;步骤5由q5完成,最后在q6中输出结果。
三、通过这次实习以及在实习中学到的理解,能够感受到变量消元法的独特性。变量消元法通过对联合分布的分解使得运算局部化从而降低推理复杂度。在变量众多的网络中,这种运算量的降低可能是指数级的,与贝叶斯网的节点度有关。
四、同时,通过在本次实习的资料搜索中,发现变量消除法还是存在一些缺点。(1)算法没有对中间变量存储的功能, 因此存在大量重复计算;(2)变量消除的顺序很大程度影响计算效率,而找到最优的变量消除顺序是NP-Hard问题。
其中最耗费时间和空间的步骤是对Elim(F,Z)的调用,因此可以把这一步的复杂度作为整个算法的复杂度,从而优化整个算法。
同时,还可以选择变量消除顺序,不过,选择 VE 的最佳顺序是 NP 难问题。 但是,在实践中,可以会采取以下启发式方法:(1)最小邻居:选择依赖变量最少的变量。(2)最小权重:选择变量来最小化其依赖变量基数的乘积。(3)最小填充:选择节点来最小化要添加到图形中的因子数量。