数组篇刷题总结

二分查找：

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
 

提示：

你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/binary-search
 

代码：

class Solution 
{
public:
    int search(vector& nums, int target) 
    {
       //闭区间[leftPos,rightPos]、[1,1]
    //    int leftPos = 0;
    //    int rightPos = nums.size() - 1;
    //    int mid;

    //     while(leftPos <= rightPos)
    //     {
    //         mid = (leftPos + rightPos) / 2;
    //         if(nums[mid] > target)
    //         {
    //             rightPos = mid - 1;
    //         }else if(nums[mid] < target)
    //         {
    //             leftPos = mid + 1;
    //         }else
    //         {
    //             return mid;
    //         }
    //     }

    //     return -1;
    // }
        int leftPos = 0;
        int rightPos = nums.size();
        int mid;

        while(leftPos < rightPos)
        {
            mid = (leftPos + rightPos) / 2;
            if(nums[mid] > target)
            {
                rightPos = mid;
            }else if(nums[mid] < target)
            {
                leftPos = mid + 1;
            }else
            {
                return mid;
            }
        }

        return -1;
    }
    
};

移除元素：

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

说明:

为什么返回数值是整数，但输出的答案是数组呢?

请注意，输入数组是以「引用」方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

你可以想象内部操作如下:

// nums 是以“引用”方式传递的。也就是说，不对实参作任何拷贝
int len = removeElement(nums, val);

// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
    print(nums[i]);
}
 

示例 1：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]
解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。
示例 2：

输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3]
解释：函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
 

提示：

0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/remove-element
 

代码：

class Solution 
{
public:
    int removeElement(vector& nums, int val) 
    {
        int fast;//快指针
        int slow = 0;//慢指针

        for(int fast = 0; fast < nums.size(); fast++)
        {
            if(nums[fast] != val)
            {
                nums[slow++] = nums[fast];
            }
        }

        return slow;
    }
};

有序数组的平方：

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]
示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]
 

提示：

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 已按 非递减顺序 排序
 

进阶：

请你设计时间复杂度为 O(n) 的算法解决本问题

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/squares-of-a-sorted-array
 

代码：

class Solution 
{
    //双指针法
public:
    vector sortedSquares(vector& nums)
    {
        int i = 0;
        int j = nums.size()  - 1;
        vector array(nums.size(), 0);
        int k = array.size() - 1;

        while(i <= j)
        {
            if(nums[i] * nums[i] > nums[j] * nums[j])
            {
                array[k] = nums[i] * nums[i];
                i++;
                k--;
            }else
            {
                array[k] = nums[j] * nums[j];
                j--;
                k--;
            }
        }

        return array;
    }
};

长度最小的子数组：

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2：

输入：target = 4, nums = [1,4,4]
输出：1
示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0
 

提示：

1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/minimum-size-subarray-sum
 

代码：

class Solution 
{
public:
    int minSubArrayLen(int target, vector& nums) 
    {
        int i = 0;
        int maxLength = INT32_MAX; //将它设置为最大长度
        int sum = 0;
        int count = 0;

        for(int j = 0; j < nums.size(); j++)
        {
            sum += nums[j];
            while(sum >= target)
            {
                count = j - i + 1;
                maxLength = maxLength < count ? maxLength : count;
                sum -= nums[i++];
            }
        }

        return maxLength == INT32_MAX ? 0 : maxLength;
    }
};

螺旋矩阵II：

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

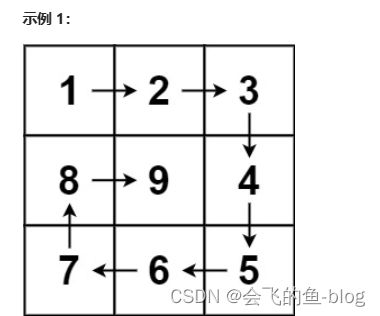
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]
示例 2：

 

输入：n = 1
输出：[[1]]
 

提示：

1 <= n <= 20

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/spiral-matrix-ii

代码：

class Solution 
{
public:
    vector> generateMatrix(int n) 
    {
        vector> res(n, vector(n, 0)); // 
        
        int startX = 0,startY = 0;
        int mid = n / 2; //最后奇数位置
        int offset = 1; //左闭右开
        int count = n / 2; //判断有几层
        int sum = 1;
        int i,j;
        while(count--)
        {
            i = startY;
            j = startX;

            for(i = startY; i < n - offset; i++)
            {
                res[startX][i] = sum++;
            }

            for(j = startX; j < n - offset; j++)
            {
                res[j][i] = sum++;
            }

            for(;i > startY; i--)
            {
                res[j][i] = sum++;
            }

            for(;j > startX; j--)
            {
                res[j][i] = sum++;
            }

            startX++;
            startY++;
            offset++;
        }

        if(n % 2)
        {
            res[mid][mid] = sum;
        }

        return res;

    }
};