团体程序设计天梯赛-练习集 (L2-021 - L2-040)
L2-021 点赞狂魔 排序
微博上有个“点赞”功能,你可以为你喜欢的博文点个赞表示支持。每篇博文都有一些刻画其特性的标签,而你点赞的博文的类型,也间接刻画了你的特性。然而有这么一种人,他们会通过给自己看到的一切内容点赞来狂刷存在感,这种人就被称为“点赞狂魔”。他们点赞的标签非常分散,无法体现出明显的特性。本题就要求你写个程序,通过统计每个人点赞的不同标签的数量,找出前3名点赞狂魔。
输入格式:
输入在第一行给出一个正整数N(≤100),是待统计的用户数。随后N行,每行列出一位用户的点赞标签。格式为“Name K F1⋯FK”,其中Name是不超过8个英文小写字母的非空用户名,1≤K≤1000,Fi(i=1,⋯,K)是特性标签的编号,我们将所有特性标签从 1 到 107 编号。数字间以空格分隔。
输出格式:
统计每个人点赞的不同标签的数量,找出数量最大的前3名,在一行中顺序输出他们的用户名,其间以1个空格分隔,且行末不得有多余空格。如果有并列,则输出标签出现次数平均值最小的那个,题目保证这样的用户没有并列。若不足3人,则用-补齐缺失,例如mike jenny -就表示只有2人。
输入样例:
5
bob 11 101 102 103 104 105 106 107 108 108 107 107
peter 8 1 2 3 4 3 2 5 1
chris 12 1 2 3 4 5 6 7 8 9 1 2 3
john 10 8 7 6 5 4 3 2 1 7 5
jack 9 6 7 8 9 10 11 12 13 14
输出样例:
jack chris john
分析:
简单的结构体排序,利用结构体存数据,排序后输出前3位即可
坑:标签出现次数平均值就是k
代码:
#includeL2-022 重排链表 模拟链表
给定一个单链表 L1→L2→⋯→Ln−1→Ln,请编写程序将链表重新排列为 Ln→L1→Ln−1→L2→⋯。例如:给定L为1→2→3→4→5→6,则输出应该为6→1→5→2→4→3。
输入格式:
每个输入包含1个测试用例。每个测试用例第1行给出第1个结点的地址和结点总个数,即正整数N (≤105)。结点的地址是5位非负整数,NULL地址用−1表示。
接下来有N行,每行格式为:
Address Data Next
其中Address是结点地址;Data是该结点保存的数据,为不超过105的正整数;Next是下一结点的地址。题目保证给出的链表上至少有两个结点。
输出格式:
对每个测试用例,顺序输出重排后的结果链表,其上每个结点占一行,格式与输入相同。
输入样例:
00100 6
00000 4 99999
00100 1 12309
68237 6 -1
33218 3 00000
99999 5 68237
12309 2 33218
输出样例:
68237 6 00100
00100 1 99999
99999 5 12309
12309 2 00000
00000 4 33218
33218 3 -1
分析:
用数组模拟链表,用一个指针即可实现重排输出。
坑:输入数据中可能不止一个点的下一地址为-1;
代码:
#includeL2-023 图着色问题 简单图
图着色问题是一个著名的NP完全问题。给定无向图G=(V,E),问可否用K种颜色为V中的每一个顶点分配一种颜色,使得不会有两个相邻顶点具有同一种颜色?
但本题并不是要你解决这个着色问题,而是对给定的一种颜色分配,请你判断这是否是图着色问题的一个解。
输入格式:
输入在第一行给出3个整数V(0<V≤500)、E(≥0)和K(0<K≤V),分别是无向图的顶点数、边数、以及颜色数。顶点和颜色都从1到V编号。随后E行,每行给出一条边的两个端点的编号。在图的信息给出之后,给出了一个正整数N(≤20),是待检查的颜色分配方案的个数。随后N行,每行顺次给出V个顶点的颜色(第i个数字表示第i个顶点的颜色),数字间以空格分隔。题目保证给定的无向图是合法的(即不存在自回路和重边)。
输出格式:
对每种颜色分配方案,如果是图着色问题的一个解则输出Yes,否则输出No,每句占一行。
输入样例:
6 8 3
2 1
1 3
4 6
2 5
2 4
5 4
5 6
3 6
4
1 2 3 3 1 2
4 5 6 6 4 5
1 2 3 4 5 6
2 3 4 2 3 4
输出样例:
Yes
Yes
No
No
分析:
简单题,存好边和点的颜色后,遍历所有边即可,用邻接表存更优。
坑:实际用的颜色和初始给出的颜色数目要一样
代码:
#includeL2-024 部落 并查集
在一个社区里,每个人都有自己的小圈子,还可能同时属于很多不同的朋友圈。我们认为朋友的朋友都算在一个部落里,于是要请你统计一下,在一个给定社区中,到底有多少个互不相交的部落?并且检查任意两个人是否属于同一个部落。
输入格式:
输入在第一行给出一个正整数N(≤104),是已知小圈子的个数。随后N行,每行按下列格式给出一个小圈子里的人:
K P[1] P[2] ⋯ P[K]
其中K是小圈子里的人数,P[i](i=1,⋯,K)是小圈子里每个人的编号。这里所有人的编号从1开始连续编号,最大编号不会超过104。
之后一行给出一个非负整数Q(≤104),是查询次数。随后Q行,每行给出一对被查询的人的编号。
输出格式:
首先在一行中输出这个社区的总人数、以及互不相交的部落的个数。随后对每一次查询,如果他们属于同一个部落,则在一行中输出Y,否则输出N。
输入样例:
4
3 10 1 2
2 3 4
4 1 5 7 8
3 9 6 4
2
10 5
3 7
输出样例:
10 2
Y
N
分析:
并查集简单题,将同一个部落的人合并和统计部落数,按要求查找并比较他们的祖先
代码:
#includeL2-025 分而治之 并查集
分而治之,各个击破是兵家常用的策略之一。在战争中,我们希望首先攻下敌方的部分城市,使其剩余的城市变成孤立无援,然后再分头各个击破。为此参谋部提供了若干打击方案。本题就请你编写程序,判断每个方案的可行性。
输入格式:
输入在第一行给出两个正整数 N 和 M(均不超过10 000),分别为敌方城市个数(于是默认城市从 1 到 N 编号)和连接两城市的通路条数。随后 M 行,每行给出一条通路所连接的两个城市的编号,其间以一个空格分隔。在城市信息之后给出参谋部的系列方案,即一个正整数 K (≤ 100)和随后的 K 行方案,每行按以下格式给出:
Np v[1] v[2] ... v[Np]
其中 Np 是该方案中计划攻下的城市数量,后面的系列 v[i] 是计划攻下的城市编号。
输出格式:
对每一套方案,如果可行就输出YES,否则输出NO。
输入样例:
10 11
8 7
6 8
4 5
8 4
8 1
1 2
1 4
9 8
9 1
1 10
2 4
5
4 10 3 8 4
6 6 1 7 5 4 9
3 1 8 4
2 2 8
7 9 8 7 6 5 4 2
输出样例:
NO
YES
YES
NO
NO
分析:
先将所有边记录下来,再每次询问时,用并查集处理所有没被摧毁的边,记录连通块即fa[x]=x的数量与没被摧毁的城市数量比较
代码:
#includeL2-026 小字辈 递归
本题给定一个庞大家族的家谱,要请你给出最小一辈的名单。
输入格式:
输入在第一行给出家族人口总数 N(不超过 100 000 的正整数) —— 简单起见,我们把家族成员从 1 到 N 编号。随后第二行给出 N 个编号,其中第 i 个编号对应第 i 位成员的父/母。家谱中辈分最高的老祖宗对应的父/母编号为 -1。一行中的数字间以空格分隔。
输出格式:
首先输出最小的辈分(老祖宗的辈分为 1,以下逐级递增)。然后在第二行按递增顺序输出辈分最小的成员的编号。编号间以一个空格分隔,行首尾不得有多余空格。
输入样例:
9
2 6 5 5 -1 5 6 4 7
输出样例:
4
1 9
分析:
先计算出所有人辈分(本文利用递归),再找到所有最小辈分的人
代码:
#includeL2-027 名人堂与代金券 排序
对于在中国大学MOOC(http://www.icourse163.org/ )学习“数据结构”课程的学生,想要获得一张合格证书,总评成绩必须达到 60 分及以上,并且有另加福利:总评分在 [G, 100] 区间内者,可以得到 50 元 PAT 代金券;在 [60, G) 区间内者,可以得到 20 元PAT代金券。全国考点通用,一年有效。同时任课老师还会把总评成绩前 K 名的学生列入课程“名人堂”。本题就请你编写程序,帮助老师列出名人堂的学生,并统计一共发出了面值多少元的 PAT 代金券。
输入格式:
输入在第一行给出 3 个整数,分别是 N(不超过 10 000 的正整数,为学生总数)、G(在(60,100) 区间内的整数,为题面中描述的代金券等级分界线)、K(不超过 100且不超过 N 的正整数,为进入名人堂的最低名次)。接下来 N 行,每行给出一位学生的账号(长度不超过15位、不带空格的字符串)和总评成绩(区间 [0, 100] 内的整数),其间以空格分隔。题目保证没有重复的账号。
输出格式:
首先在一行中输出发出的 PAT 代金券的总面值。然后按总评成绩非升序输出进入名人堂的学生的名次、账号和成绩,其间以 1 个空格分隔。需要注意的是:成绩相同的学生享有并列的排名,排名并列时,按账号的字母序升序输出。
输入样例:
10 80 5
[email protected] 78
[email protected] 87
[email protected] 65
[email protected] 96
[email protected] 39
[email protected] 87
[email protected] 80
[email protected] 88
[email protected] 80
[email protected] 70
输出样例:
360
1 [email protected] 96
2 [email protected] 88
3 [email protected] 87
3 [email protected] 87
5 [email protected] 80
5 [email protected] 80
分析:
水题,直接结构体存数据再排序就好,注意排名可以并列即可
代码:
因为用的数据结构不同,所以代码有所不同,区别在于重载处比较的写法
string存邮箱
#includechar存邮箱
#includeL2-028 秀恩爱分得快 模拟
古人云:秀恩爱,分得快。
互联网上每天都有大量人发布大量照片,我们通过分析这些照片,可以分析人与人之间的亲密度。如果一张照片上出现了 K 个人,这些人两两间的亲密度就被定义为 1/K。任意两个人如果同时出现在若干张照片里,他们之间的亲密度就是所有这些同框照片对应的亲密度之和。下面给定一批照片,请你分析一对给定的情侣,看看他们分别有没有亲密度更高的异性朋友?
输入格式:
输入在第一行给出 2 个正整数:N(不超过1000,为总人数——简单起见,我们把所有人从 0 到 N-1 编号。为了区分性别,我们用编号前的负号表示女性)和 M(不超过1000,为照片总数)。随后 M 行,每行给出一张照片的信息,格式如下:
K P[1] ... P[K]
其中 K(≤ 500)是该照片中出现的人数,P[1] ~ P[K] 就是这些人的编号。最后一行给出一对异性情侣的编号 A 和 B。同行数字以空格分隔。题目保证每个人只有一个性别,并且不会在同一张照片里出现多次。
输出格式:
首先输出 A PA,其中 PA 是与 A 最亲密的异性。如果 PA 不唯一,则按他们编号的绝对值递增输出;然后类似地输出 B PB。但如果 A 和 B 正是彼此亲密度最高的一对,则只输出他们的编号,无论是否还有其他人并列。
输入样例 1:
10 4
4 -1 2 -3 4
4 2 -3 -5 -6
3 2 4 -5
3 -6 0 2
-3 2
输出样例 1:
-3 2
2 -5
2 -6
输入样例 2:
4 4
4 -1 2 -3 0
2 0 -3
2 2 -3
2 -1 2
-3 2
输出样例 2:
-3 2
代码:
#include L2-029 特立独行的幸福 数学
对一个十进制数的各位数字做一次平方和,称作一次迭代。如果一个十进制数能通过若干次迭代得到 1,就称该数为幸福数。1 是一个幸福数。此外,例如 19 经过 1 次迭代得到 82,2 次迭代后得到 68,3 次迭代后得到 100,最后得到 1。则 19 就是幸福数。显然,在一个幸福数迭代到 1 的过程中经过的数字都是幸福数,它们的幸福是依附于初始数字的。例如 82、68、100 的幸福是依附于 19 的。而一个特立独行的幸福数,是在一个有限的区间内不依附于任何其它数字的;其独立性就是依附于它的的幸福数的个数。如果这个数还是个素数,则其独立性加倍。例如 19 在区间[1, 100] 内就是一个特立独行的幸福数,其独立性为 2×4=8。
另一方面,如果一个大于1的数字经过数次迭代后进入了死循环,那这个数就不幸福。例如 29 迭代得到 85、89、145、42、20、4、16、37、58、89、…… 可见 89 到 58 形成了死循环,所以 29 就不幸福。
本题就要求你编写程序,列出给定区间内的所有特立独行的幸福数和它的独立性。
输入格式:
输入在第一行给出闭区间的两个端点:1<A<B≤104。
输出格式:
按递增顺序列出给定闭区间 [A,B] 内的所有特立独行的幸福数和它的独立性。每对数字占一行,数字间以 1 个空格分隔。
如果区间内没有幸福数,则在一行中输出 SAD。
输入样例 1:
10 40
输出样例 1:
19 8
23 6
28 3
31 4
32 3
**注意:**样例中,10、13 也都是幸福数,但它们分别依附于其他数字(如 23、31 等等),所以不输出。其它数字虽然其实也依附于其它幸福数,但因为那些数字不在给定区间 [10, 40] 内,所以它们在给定区间内是特立独行的幸福数。
输入样例 2:
110 120
输出样例 2:
SAD
代码:
#includeL2-031 深入虎穴 dfs
著名的王牌间谍 007 需要执行一次任务,获取敌方的机密情报。已知情报藏在一个地下迷宫里,迷宫只有一个入口,里面有很多条通路,每条路通向一扇门。每一扇门背后或者是一个房间,或者又有很多条路,同样是每条路通向一扇门…… 他的手里有一张表格,是其他间谍帮他收集到的情报,他们记下了每扇门的编号,以及这扇门背后的每一条通路所到达的门的编号。007 发现不存在两条路通向同一扇门。
内线告诉他,情报就藏在迷宫的最深处。但是这个迷宫太大了,他需要你的帮助 —— 请编程帮他找出距离入口最远的那扇门。
输入格式:
输入首先在一行中给出正整数 N(<105),是门的数量。最后 N 行,第 i 行(1≤i≤N)按以下格式描述编号为 i 的那扇门背后能通向的门:
K D[1] D[2] ... D[K]
其中 K 是通道的数量,其后是每扇门的编号。
输出格式:
在一行中输出距离入口最远的那扇门的编号。题目保证这样的结果是唯一的。
输入样例:
13
3 2 3 4
2 5 6
1 7
1 8
1 9
0
2 11 10
1 13
0
0
1 12
0
0
输出样例:
12
代码:
#includeL2-032 彩虹瓶 栈
彩虹瓶的制作过程(并不)是这样的:先把一大批空瓶铺放在装填场地上,然后按照一定的顺序将每种颜色的小球均匀撒到这批瓶子里。
假设彩虹瓶里要按顺序装 N 种颜色的小球(不妨将顺序就编号为 1 到 N)。现在工厂里有每种颜色的小球各一箱,工人需要一箱一箱地将小球从工厂里搬到装填场地。如果搬来的这箱小球正好是可以装填的颜色,就直接拆箱装填;如果不是,就把箱子先码放在一个临时货架上,码放的方法就是一箱一箱堆上去。当一种颜色装填完以后,先看看货架顶端的一箱是不是下一个要装填的颜色,如果是就取下来装填,否则去工厂里再搬一箱过来。
如果工厂里发货的顺序比较好,工人就可以顺利地完成装填。例如要按顺序装填 7 种颜色,工厂按照 7、6、1、3、2、5、4 这个顺序发货,则工人先拿到 7、6 两种不能装填的颜色,将其按照 7 在下、6 在上的顺序堆在货架上;拿到 1 时可以直接装填;拿到 3 时又得临时码放在 6 号颜色箱上;拿到 2 时可以直接装填;随后从货架顶取下 3 进行装填;然后拿到 5,临时码放到 6 上面;最后取了 4 号颜色直接装填;剩下的工作就是顺序从货架上取下 5、6、7 依次装填。
但如果工厂按照 3、1、5、4、2、6、7 这个顺序发货,工人就必须要愤怒地折腾货架了,因为装填完 2 号颜色以后,不把货架上的多个箱子搬下来就拿不到 3 号箱,就不可能顺利完成任务。
另外,货架的容量有限,如果要堆积的货物超过容量,工人也没办法顺利完成任务。例如工厂按照 7、6、5、4、3、2、1 这个顺序发货,如果货架够高,能码放 6 只箱子,那还是可以顺利完工的;但如果货架只能码放 5 只箱子,工人就又要愤怒了……
本题就请你判断一下,工厂的发货顺序能否让工人顺利完成任务。
输入格式:
输入首先在第一行给出 3 个正整数,分别是彩虹瓶的颜色数量 N(1<N≤103)、临时货架的容量 M(<N)、以及需要判断的发货顺序的数量 K。
随后 K 行,每行给出 N 个数字,是 1 到N 的一个排列,对应工厂的发货顺序。
一行中的数字都以空格分隔。
输出格式:
对每个发货顺序,如果工人可以愉快完工,就在一行中输出 YES;否则输出 NO。
输入样例:
7 5 3
7 6 1 3 2 5 4
3 1 5 4 2 6 7
7 6 5 4 3 2 1
输出样例:
YES
NO
NO
代码:
#includeL2-033 简单计算器 栈
本题要求你为初学数据结构的小伙伴设计一款简单的利用堆栈执行的计算器。如上图所示,计算器由两个堆栈组成,一个堆栈 S1 存放数字,另一个堆栈 S2 存放运算符。计算器的最下方有一个等号键,每次按下这个键,计算器就执行以下操作:
- 从 S1 中弹出两个数字,顺序为 n1 和 n2;
- 从 S2 中弹出一个运算符 op;
- 执行计算 n2 op n1;
- 将得到的结果压回 S1。
直到两个堆栈都为空时,计算结束,最后的结果将显示在屏幕上。
输入格式:
输入首先在第一行给出正整数 N(1<N≤103),为 S1 中数字的个数。
第二行给出 N 个绝对值不超过 100 的整数;第三行给出 N−1 个运算符 —— 这里仅考虑 +、-、*、/ 这四种运算。一行中的数字和符号都以空格分隔。
输出格式:
将输入的数字和运算符按给定顺序分别压入堆栈 S1 和 S2,将执行计算的最后结果输出。注意所有的计算都只取结果的整数部分。题目保证计算的中间和最后结果的绝对值都不超过 109。
如果执行除法时出现分母为零的非法操作,则在一行中输出:ERROR: X/0,其中 X 是当时的分子。然后结束程序。
输入样例 1:
5
40 5 8 3 2
/ * - +
输出样例 1:
2
输入样例 2:
5
2 5 8 4 4
* / - +
输出样例 2:
ERROR: 5/0
代码:
#include
if ( sc.top() == '+' ) ans = n2 + n1;
if ( sc.top() == '-' ) ans = n2 - n1;
if ( sc.top() == '*' ) ans = n2 * n1;
if ( sc.top() == '/' ) {
if ( n1 == 0){
printf("ERROR: %d/0\n", n2);
return ;
}
ans = n2 / n1;
}
sc.pop();
si.push(ans);
}
printf("%d\n", si.top());
}
int main(){
int n; scanf("%d",&n);
vector<int> vi;
vector<char> vc;
for ( int i = 1 ; i <= n ; i ++ ){
int x; scanf("%d", &x);
vi.push_back(x);
}
for ( int i = 1 ; i < n ; i ++ ){
char c[5]; scanf("%s", c);
vc.push_back(c[0]);
}
fun(vi, vc);
return 0;
}
L2-035 完全二叉树的层序遍历 树
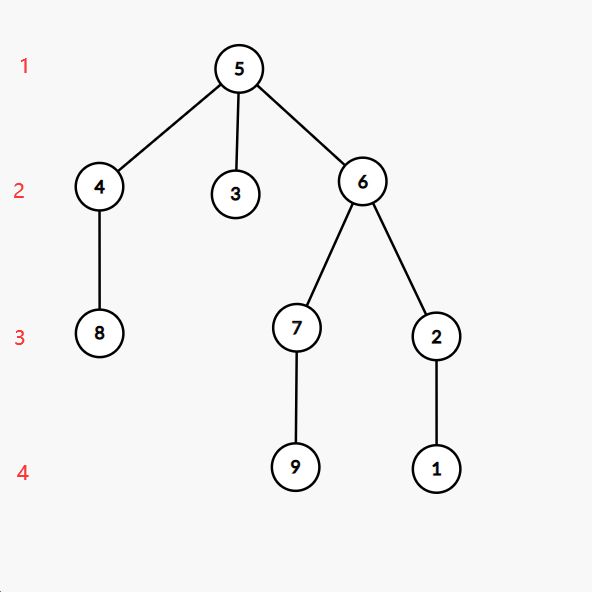
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是完美二叉树。对于深度为 D 的,有 N 个结点的二叉树,若其结点对应于相同深度完美二叉树的层序遍历的前 N 个结点,这样的树就是完全二叉树。
给定一棵完全二叉树的后序遍历,请你给出这棵树的层序遍历结果。
输入格式:
输入在第一行中给出正整数 N(≤30),即树中结点个数。第二行给出后序遍历序列,为 N 个不超过 100 的正整数。同一行中所有数字都以空格分隔。
输出格式:
在一行中输出该树的层序遍历序列。所有数字都以 1 个空格分隔,行首尾不得有多余空格。
输入样例:
8
91 71 2 34 10 15 55 18
输出样例:
18 34 55 71 2 10 15 91
分析:
完全二叉树采用顺序存储方式,如果有左孩子,则编号为2i,如果有右孩子,编号为2i+1,然后按照后序遍历的方式(左右根),进行输入,最后顺序输出即可
代码:
#includeL2-036 网红点打卡攻略 模拟
一个旅游景点,如果被带火了的话,就被称为“网红点”。大家来网红点游玩,俗称“打卡”。在各个网红点打卡的快(省)乐(钱)方法称为“攻略”。你的任务就是从一大堆攻略中,找出那个能在每个网红点打卡仅一次、并且路上花费最少的攻略。
输入格式:
首先第一行给出两个正整数:网红点的个数 N(1<N≤200)和网红点之间通路的条数 M。随后 M 行,每行给出有通路的两个网红点、以及这条路上的旅行花费(为正整数),格式为“网红点1 网红点2 费用”,其中网红点从 1 到 N 编号;同时也给出你家到某些网红点的花费,格式相同,其中你家的编号固定为 0。
再下一行给出一个正整数 K,是待检验的攻略的数量。随后 K 行,每行给出一条待检攻略,格式为:
n V1 V2 ⋯ V**n
其中 n(≤200) 是攻略中的网红点数,V**i 是路径上的网红点编号。这里假设你从家里出发,从 V1 开始打卡,最后从 V**n 回家。
输出格式:
在第一行输出满足要求的攻略的个数。
在第二行中,首先输出那个能在每个网红点打卡仅一次、并且路上花费最少的攻略的序号(从 1 开始),然后输出这个攻略的总路费,其间以一个空格分隔。如果这样的攻略不唯一,则输出序号最小的那个。
题目保证至少存在一个有效攻略,并且总路费不超过 109。
输入样例:
6 13
0 5 2
6 2 2
6 0 1
3 4 2
1 5 2
2 5 1
3 1 1
4 1 2
1 6 1
6 3 2
1 2 1
4 5 3
2 0 2
7
6 5 1 4 3 6 2
6 5 2 1 6 3 4
8 6 2 1 6 3 4 5 2
3 2 1 5
6 6 1 3 4 5 2
7 6 2 1 3 4 5 2
6 5 2 1 4 3 6
输出样例:
3
5 11
样例说明:
第 2、3、4、6 条都不满足攻略的基本要求,即不能做到从家里出发,在每个网红点打卡仅一次,且能回到家里。所以满足条件的攻略有 3 条。
第 1 条攻略的总路费是:(0->5) 2 + (5->1) 2 + (1->4) 2 + (4->3) 2 + (3->6) 2 + (6->2) 2 + (2->0) 2 = 14;
第 5 条攻略的总路费同理可算得:1 + 1 + 1 + 2 + 3 + 1 + 2 = 11,是一条更省钱的攻略;
第 7 条攻略的总路费同理可算得:2 + 1 + 1 + 2 + 2 + 2 + 1 = 11,与第 5 条花费相同,但序号较大,所以不输出。
代码:
#includeL2-037 包装机 栈和队列
一种自动包装机的结构如图 1 所示。首先机器中有 N 条轨道,放置了一些物品。轨道下面有一个筐。当某条轨道的按钮被按下时,活塞向左推动,将轨道尽头的一件物品推落筐中。当 0 号按钮被按下时,机械手将抓取筐顶部的一件物品,放到流水线上。图 2 显示了顺序按下按钮 3、2、3、0、1、2、0 后包装机的状态。
图1 自动包装机的结构
图 2 顺序按下按钮 3、2、3、0、1、2、0 后包装机的状态
一种特殊情况是,因为筐的容量是有限的,当筐已经满了,但仍然有某条轨道的按钮被按下时,系统应强制启动 0 号键,先从筐里抓出一件物品,再将对应轨道的物品推落。此外,如果轨道已经空了,再按对应的按钮不会发生任何事;同样的,如果筐是空的,按 0 号按钮也不会发生任何事。
现给定一系列按钮操作,请你依次列出流水线上的物品。
输入格式:
输入第一行给出 3 个正整数 N(≤100)、M(≤1000)和 Smax(≤100),分别为轨道的条数(于是轨道从 1 到 N 编号)、每条轨道初始放置的物品数量、以及筐的最大容量。随后 N 行,每行给出 M 个英文大写字母,表示每条轨道的初始物品摆放。
最后一行给出一系列数字,顺序对应被按下的按钮编号,直到 −1 标志输入结束,这个数字不要处理。数字间以空格分隔。题目保证至少会取出一件物品放在流水线上。
输出格式:
在一行中顺序输出流水线上的物品,不得有任何空格。
输入样例:
3 4 4
GPLT
PATA
OMSA
3 2 3 0 1 2 0 2 2 0 -1
输出样例:
MATA
分析:
队列模拟传送带,栈模拟筐
代码:
#includeL2-038 病毒溯源 dfs
病毒容易发生变异。某种病毒可以通过突变产生若干变异的毒株,而这些变异的病毒又可能被诱发突变产生第二代变异,如此继续不断变化。
现给定一些病毒之间的变异关系,要求你找出其中最长的一条变异链。
在此假设给出的变异都是由突变引起的,不考虑复杂的基因重组变异问题 —— 即每一种病毒都是由唯一的一种病毒突变而来,并且不存在循环变异的情况。
输入格式:
输入在第一行中给出一个正整数 N(≤104),即病毒种类的总数。于是我们将所有病毒从 0 到 N−1 进行编号。
随后 N 行,每行按以下格式描述一种病毒的变异情况:
k 变异株1 …… 变异株k
其中 k 是该病毒产生的变异毒株的种类数,后面跟着每种变异株的编号。第 i 行对应编号为 i 的病毒(0≤i<N)。题目保证病毒源头有且仅有一个。
输出格式:
首先输出从源头开始最长变异链的长度。
在第二行中输出从源头开始最长的一条变异链,编号间以 1 个空格分隔,行首尾不得有多余空格。如果最长链不唯一,则输出最小序列。
注:我们称序列 { a1,⋯,a**n } 比序列 { b1,⋯,b**n } “小”,如果存在 1≤k≤n 满足 a**i=b**i 对所有 i<k 成立,且 a**k<b**k。
输入样例:
10
3 6 4 8
0
0
0
2 5 9
0
1 7
1 2
0
2 3 1
输出样例:
4
0 4 9 1
代码:
#includeL2-039 清点代码库 排序
上图转自新浪微博:“阿里代码库有几亿行代码,但其中有很多功能重复的代码,比如单单快排就被重写了几百遍。请设计一个程序,能够将代码库中所有功能重复的代码找出。各位大佬有啥想法,我当时就懵了,然后就挂了。。。”
这里我们把问题简化一下:首先假设两个功能模块如果接受同样的输入,总是给出同样的输出,则它们就是功能重复的;其次我们把每个模块的输出都简化为一个整数(在 int 范围内)。于是我们可以设计一系列输入,检查所有功能模块的对应输出,从而查出功能重复的代码。你的任务就是设计并实现这个简化问题的解决方案。
输入格式:
输入在第一行中给出 2 个正整数,依次为 N(≤104)和 M(≤102),对应功能模块的个数和系列测试输入的个数。
随后 N 行,每行给出一个功能模块的 M 个对应输出,数字间以空格分隔。
输出格式:
首先在第一行输出不同功能的个数 K。随后 K 行,每行给出具有这个功能的模块的个数,以及这个功能的对应输出。数字间以 1 个空格分隔,行首尾不得有多余空格。输出首先按模块个数非递增顺序,如果有并列,则按输出序列的递增序给出。
注:所谓数列 { A1, …, A**M } 比 { B1, …, B**M } 大,是指存在 1≤i<M,使得 A1=B1,…,A**i=B**i 成立,且 A**i+1>B**i+1。
输入样例:
7 3
35 28 74
-1 -1 22
28 74 35
-1 -1 22
11 66 0
35 28 74
35 28 74
输出样例:
4
3 35 28 74
2 -1 -1 22
1 11 66 0
1 28 74 35
代码:
#includeL2-040 哲哲打游戏 模拟
哲哲是一位硬核游戏玩家。最近一款名叫《达诺达诺》的新游戏刚刚上市,哲哲自然要快速攻略游戏,守护硬核游戏玩家的一切!
为简化模型,我们不妨假设游戏有 N 个剧情点,通过游戏里不同的操作或选择可以从某个剧情点去往另外一个剧情点。此外,游戏还设置了一些存档,在某个剧情点可以将玩家的游戏进度保存在一个档位上,读取存档后可以回到剧情点,重新进行操作或者选择,到达不同的剧情点。
为了追踪硬核游戏玩家哲哲的攻略进度,你打算写一个程序来完成这个工作。假设你已经知道了游戏的全部剧情点和流程,以及哲哲的游戏操作,请你输出哲哲的游戏进度。
输入格式:
输入第一行是两个正整数 N 和 M (1≤N,M≤105),表示总共有 N 个剧情点,哲哲有 M 个游戏操作。
接下来的 N 行,每行对应一个剧情点的发展设定。第 i 行的第一个数字是 K**i,表示剧情点 i 通过一些操作或选择能去往下面 K**i 个剧情点;接下来有 K**i 个数字,第 k 个数字表示做第 k 个操作或选择可以去往的剧情点编号。
最后有 M 行,每行第一个数字是 0、1 或 2,分别表示:
- 0 表示哲哲做出了某个操作或选择,后面紧接着一个数字 j,表示哲哲在当前剧情点做出了第 j 个选择。我们保证哲哲的选择永远是合法的。
- 1 表示哲哲进行了一次存档,后面紧接着是一个数字 j,表示存档放在了第 j 个档位上。
- 2 表示哲哲进行了一次读取存档的操作,后面紧接着是一个数字 j,表示读取了放在第 j 个位置的存档。
约定:所有操作或选择以及剧情点编号都从 1 号开始。存档的档位不超过 100 个,编号也从 1 开始。游戏默认从 1 号剧情点开始。总的选项数(即 ∑K**i)不超过 106。
输出格式:
对于每个 1(即存档)操作,在一行中输出存档的剧情点编号。
最后一行输出哲哲最后到达的剧情点编号。
输入样例:
10 11
3 2 3 4
1 6
3 4 7 5
1 3
1 9
2 3 5
3 1 8 5
1 9
2 8 10
0
1 1
0 3
0 1
1 2
0 2
0 2
2 2
0 3
0 1
1 1
0 2
输出样例:
1
3
9
10
样例解释:
简单给出样例中经过的剧情点顺序:
1 -> 4 -> 3 -> 7 -> 8 -> 3 -> 5 -> 9 -> 10。
档位 1 开始存的是 1 号剧情点;档位 2 存的是 3 号剧情点;档位 1 后来又存了 9 号剧情点。
代码:
#include