Direct3D 12——几何着色器——几何着色器概念

几何着色器

几何着色器这个可选阶段便位于顶点着色器与像素着色器之间。几何着色器所输出的图元由顶点列表定义而成。在退岀几何着色器时，必将顶点的位置变换到齐次 裁剪空间。换言之，经过几何着色器阶段的处理后，我们就得到了位于齐次裁剪空间中由一系列顶点所 定义的多个图元。这些顶点会同样历经投影(齐次除法)与光栅化等后续步骤。

几何着色器的一般编写格式：

[maxvertexcount(N)]
void ShaderName (PrimitiveType InputVertexType InputName[NumElements],
inout StreamOutputObject<OutputVertexType> OutputName）
（
//几何着色器的具体实现
}

我们必须先指定几何着色器单次调用所输出的顶点数量最大值（每个图元都会调用一次几何着色器, 走一遍其中的处理流程）。对此，可以使用下列属性语法来设置着色器定义之前的最大顶点数量：

[maxvertexcount（N）]

其中，N是几何着色器单次调用所输出的顶点数量最大值。几何着色器每次输岀的顶点个数都可能各不相同，但是这个数量却不能超过之前定义的最大值。出于对性能方面的考量，我们应当令 maxvertexcount的值尽可能地小。在GS（即几何着色器的缩写,geometry shader ）每次输出的标量数量在1〜20时，它将发挥出最佳的性能；而当GS每次输出的标量数量保持在 27〜40时，它的性能将下降到峰值性能的50% 。每次调用几何着色器所输岀的标量个数为： maxvertexcount与输出顶点类型结构体中标量个数的乘积L。

几何着色器输入参数必须是一个定义有特定图元的顶点数组——点应输入一个顶点、线条要 输入两个顶点、三角形需输入3个顶点、线及其邻接图元为4个顶点、三角形及其邻接图元则为6个顶 点。几何着色器的输入顶点类型即为顶点着色器输出的顶点类型（例如Vertex0ut）。输入参数一定要 以图元类型作为前缀，用以描述输入到几何着色器的具体图元类型。该前缀可以是下列类型之一：

  1.point：输入的图元为点。
  2.line：输入的图元为线列表或线条带。
  3.triangle：输入的图元为三角形列表或三角形带。
  4.lineadj :输入的图元为线列表及其邻接图元，或线条带及其邻接图元。
  5.triangleadj ：输入的图元为三角形列表及其邻接图元，或三角形带及其邻接图元。

向几何着色器输入的数据必须是完整的图元（例如组成线条的两个顶点、构成三角形的3个 顶点等）。因此，几何着色器并不会区分输入的图元究竟是列表结构（list）还是带状结构 （strip ）o举个例子，若绘制的图元实际上是三角形带，但几何着色器仍会把三角形带视作多 个三角形并分别进行单独的处理，即将每个三角形的3个顶点作为其输入数据。绘制带状结 构的过程中会产生额外的开销，因为多个图元所共用的顶点在几何着色器中会被处理多次。

输岀参数一定要标有inout修饰符。另外，它必须是一种流类型(stream typeo即某种类型的流输 出对象)。流类型存有一系列顶点，它们定义了几何着色器输出的几何图形。几何着色器可以通过内置方法Append向输岀流列表添加单个顶点：

void StreamOutputObject<OutputVertexType>::Append(OutputVertexType v);

流类型本质上是一种模板类型(template type),其模板参数用以指定输岀顶点的具体类型(如 GeoOut )。流类型有如下3种。

1.PointStream: 一系列顶点所定义的点列表。
2.LineStream: 一系列顶点所定义的线条带。
3.TriangleStream: 一系列顶点所定义的三角形带。

几何着色器输岀的多个顶点会构成图元，图元的输岀类型由流类型(即Pointstream. Linestream与TriangleStream )来指定。对于线条与三角形来说，几何着色器输岀的对应图元必 定是线条带与三角形带。而线条列表与三角形列表可借助内置函数Restartstrip来实现：

void StreamOutputObject<OutputVertexType>::Restartstrip();

mShaders["treeSpriteGS"] = d3dUtil::CompileShader(L"Shaders\\TreeSprite.hlsl", nullptr, "GS", "gs_5_0");

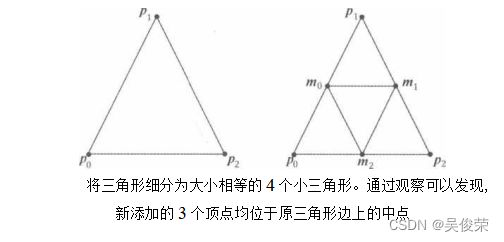
下列几何着色器详细地展示了 Append与Restartstrip方法的调用过程。此示例会将输入的三 角形进行细分,并输出细分后的4个小三角形：

struct VertexOut
{
    float3 PosL     : POSITION;
    float3 NormalL  : NORMAL;
    float2 Tex      : TEXCOORD;
};
struct GeoOut
{
	float4 PosH    : SV_POSITION;
    float3 PosW    : POSITION;
    float3 NormalW : NORMAL;
    float2 Tex    : TEXCOORD;
    float  FogLerp  : FOG;
};

void Subdivide(VertexOut inverts[3], out VertexOut outVerts[6])
{
          //         1
          //         *
          //        / \
          //       /   \
          //   m0*-------*m1
          //    / \    / \
         //    /   \  /   \
         //   *-----*------*
         //   0     m2      2
         
        VertexOut m[3];
        
      //计算三角形边上的中点
     m[0].PosL = 0.5f*(inverts[0].PosL+inVerts[1].PosL); 
     m[l].PosL = 0.5f*(inverts[1].PosL+inVerts[2].PosL);
     m[2].PosL = 0.5f*(inverts[2].PosL+inVerts[0].PosL);

      //把顶点投影到单位球面上
     m[0].PosL = normalize(m[0].PosL); 
     m[1].PosL = normalize(m[1].PosL); 
     m[2].PosL = normalize(m[2].PosL);

     //求出法线
     m[0].NormalL = m[0].PosL;
     m[1].NormalL = m[1].PosL;
     m[2].NormalL = m[2].PosL;
     
     //对纹理坐标进行插值
     m[0].Tex = 0.5f*(inverts[0].Tex+inVerts[1].Tex);
     m[1].Tex = 0.5f*(inverts[1].Tex+inVerts[2].Tex);
     m[2].Tex = 0.5f*(inverts[2].Tex+inVerts[0].Tex);

     outVerts[0] = inVerts[0];
     outVerts[1] = m[0];
     outVerts[2] = m[2];
     outVerts[3] = m[1];
     outVerts[4] = inVerts[2];
     outVerts[5] = inVerts[1];
};
void Outputsubdivision(VertexOut v[6],inout Trianglestream<GeoOut> triStream)
{
      GeoOut gout[6];
      [unroll]
      for(int i = 0; i < 6; ++i)
      {
          //将顶点变换到世界空间
          gout[i].PosW = mul(float4(v[i].PosL, 1.Of), gWorld).xyz;   
          gout[i].NormalW = mul(v[i].NormalL,(float3x3)gWorldlnvTranspose);
          
          //把顶点变换到齐次裁剪空间
          gout[i].PosH = mul(float4(v[i].PosL, 1.Of), gWorldViewProj);  
          gout[i].Tex = v[i].Tex;
      }
          //         1
          //         *
          //        / \
          //       /   \
          //   m0*-------*m1
          //    / \    / \
         //    /   \  /   \
         //   *-----*------*
         //   0     m2      2

    //我们可以将细分的小三角形绘制到两个三角形带中去：
    //	三角形带1:底端的3个三角形
    //	三角形带2:顶部的三角形
    [unroll]
    for(int j = 0; j < 5; ++j)
    {
       triStream.Append(gout[j]);
    }
    triStream.Restartstrip();
    
    triStream.Append(gout[1]);
    triStream.Append(gout[5]);
    triStream.Append(gout[3]);
}

[maxvertexcount(8)]
void GS(triangle VertexOut gin[3], inout TriangleStream<GeoOut>)
(
       VertexOut v[6];
       Subdivide(gin, v);
       Outputsubdivision(v, triStream);
}

若给出一个输入图元，几何着色器也可以根据某些条件而选择不输出任何数据。通过这 种方式，几何着色便可以轻易地“销毁”几何图形。