4.1 数据结构——串

4.1.1 串的定义 

1、定义：串（string）是由零个或多个字符组成的有限序列，又称为字符串。

一般记作：= 0)" class="mathcode" src="http://img.e-com-net.com/image/info8/cc112926001d45e990733f1698d877c3.gif" width="199" height="19">，其串中的字符数目n称为串的长度，当n = 0时，该串称为空串（null string）。

2、子串：串中任意个连续字符组成的子序列称为该串的子串。

3、主串：包含子串的串相应地称为主串。

4、字符位置：字符在序列中的序号称为该字符在串中的位置。

5、子串位置：子串第一个字符在主串中的位置。

6、空格串：有一个或多个空格组成的串，与空串不同。

7、串相等：当且仅当两个串的长度相等，并且各对应位置上的字符都相同时，这两个串是相等的。

4.1.2 串的抽象数据类型定义

ADT String
{
    数据对象：D = {ai | ai ∈ CharacterSet, i = 1, 2, ..., n, n >= 0}
    数据关系：R = { | ai-1, ai ∈ D, i = 2, 3, ..., n}
    基本操作：
        StrAssign(T, chars)          //串赋值

        StrCompare(S, T)             //串比较

        StrLength(S)                 //求串的长度

        ComCat(T, S1, S2)            //串连结

        SubString(Sub, S, pos, len)  //求子串

        StrCopy(T, S)                //串拷贝

        StrEmpty(S)                  //判断串是否为空

        ClearString(S)               //清空串

        Index(S, T, pos)             //子串的位置

        Replace(S, T, V)             //串替换

        StrInsert(S, pos, T)         //串的插入

        StrDelete(S, pos, T)         //串的删除

        DestoryStr(S)                //串销毁
}ADT String

串的存储结构：

        串中元素逻辑关系与线性表相同，串可以使用与线性表相同的存储结构，使用了顺序存储结构的串称位顺序串，使用链式存储结构的串称为链串。

4.1.3 串的顺序存储结构

#define MAXSIZE 255

typedef struct
{
    char ch[MAXSIZE + 1];   //存储串的一维数组
    int length;             //串的当前长度
}SString;

4.1.4 串的链式存储结构

//串的链式存储结构——块链结构
#define CHUNKSIZE 80    //块的大小

typedef struct Chunk
{
    char ch[CHUNKSIZE];
    struct Chunk *nexe;
}Chunk;

typedef struct
{
    Chunk *head;         //串的头指针
    Chunk *tail;         //串的尾指针
    int curlen;          //字符串中块链的长度
}LString;

4.1.5 串的模式匹配

1、算法目的：确定主串所含子串（模式串）第一次出现的位置。

2、算法种类：

BF算法（Brute-Force），又称简单匹配算法，采用穷举法的思路。

算法的思路是从S的每一个字符开始依次与T的字符进行匹配。

int Index(SString S, SString T, int pos)
{
    int i = pos;
    int j = 1;
    while (i <= S.length && j <= T.length)
    {

        if (S.ch[i] == T.ch[j])
        {
            i++;
            j++;
        }
        else
        {
            i = i - j + 2;
            j = 1;
        }
    }

    if (j >= T.length -1)
        return i - T.length;
    else 
        return -1;
}

KMP算法，是由D.E.Knuth、J.H.Morris和U.R.Pratt共同提出的，简称KMP算法。

        KMP算法的重点是当子串的某一个字符与主串不同时，主串不用回溯，子串回溯到当前字符位置之前的字符串最长前缀的下一个字符继续比较。

        一个字符串的前缀和后缀相同且长度相同且是非字符串本身，称为最长相等前后缀。

        字符串{A,B,C,A,B}的前缀集合是{A, AB, ABC, ABCA}；后缀集合是{B, AB, CAB, BCAB}。它的最长前缀是AB,长度为2，当ABCABA最后一个字符与主串不相符时，子串回溯到最长前缀的后一个字符，即C的位置，继续比较。

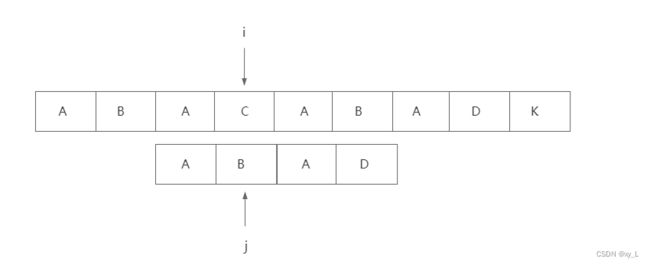
下面结合图例来讲解：

        关于主串和模式串不匹配时，j要回溯到哪个位置？

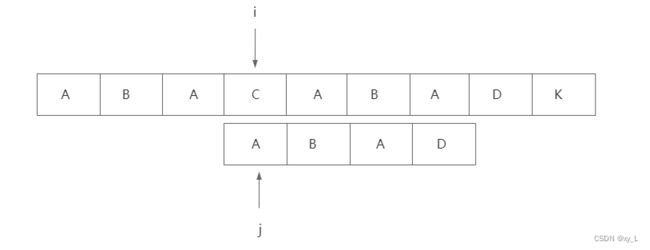
P[i] != S[j]时，j要回溯到哪个位置是重点，ABA最长相等前后缀是，所以j要回溯到1的位置，即：

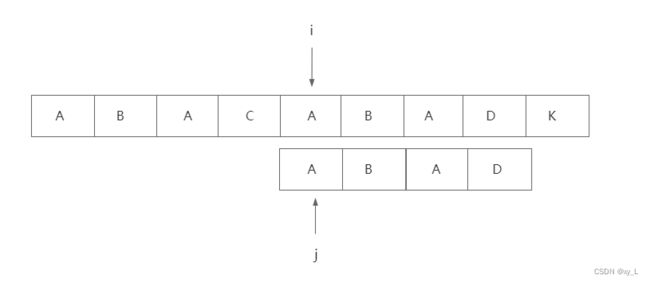
当j回溯后再进行比较 ，此时P[i] != S[j]，要继续回溯，而j前面只有一个元素，最长相等前后缀为0，所以要回溯到0这个位置，即：

再继续进行比较，发现P[i] != S[j]，此时j前已经没有元素了，i要往后移动，即：

 

 

        使用KMP算法时，我们会用一个next数组来保存子串的最长相等前后缀，而KMP算法最关键的就是求next数组。

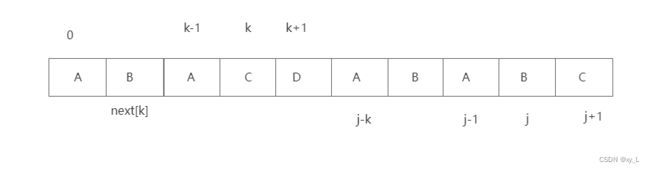
当P[k] = P[j]时，即 0 ~ k 和 j-k ~ j 的序列相同，所以有next[j+1] = next[j] + 1。

如果P[k] != P[j]呢？我们要回溯到哪个位置？要回溯到0~k-1的最长相等前后缀的位置，它的最长相等前后缀是next[k]，所以k要回溯到k=next[k]这个位置。

求next数组

因为next[0]和next[1]的最长相等前后缀都是0,为了方便计算next数组，我们将next[0] = -1。

void getNext(String ps, int next[]) {

    next[0] = -1;

    int j = 0;

    int k = -1;

    while (j < ps.length - 1) 
    {

        if (k == -1 || ps[j] == ps[k]) 
        {
           next[++j] = ++k;
        }
        else 
        {
           k = next[k];
        }

    }
}

KMP算法实现

int KMP(String ts, String ps, int pos, int len) 
{

    int i = pos; // 主串的位置

    int j = 0; // 模式串的位置

    int next[len];
    getNext(ps, next);

    while (i < ts.length && j < ps.length) 
    {

        if (j == -1 || t[i] == p[j]) 
        { 
           i++;
           j++;

        } 
        else 
        {
           j = next[j]; // j回到指定位置
        }

    }

    if (j == p.length) 
    {

       return i - ps.length;
    } 
    else 
    {
        return -1;
    }

}