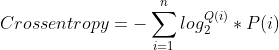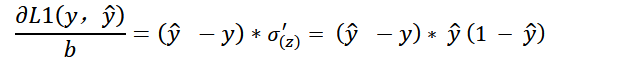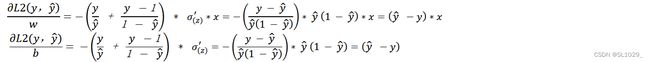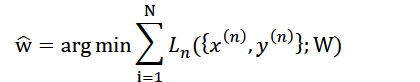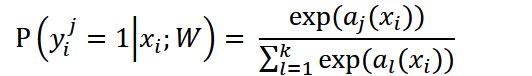图像分割——交叉熵损失

一、前言

写这篇博客的目的主要有两点，首先一点就是，以为对于交叉熵学过就会了，当初笔记也没有详细写过，但今天看论文发现里面的公式没有看懂才发现自己了解的还不够，平时用也是直接用的框架，原来一直认为会的东西其实还不会。还有一点原因就是对于语义分割任务使用交叉熵基本是固定的，但是我并不知道为什么使用交叉熵来作为损失函数，因此写下来笔记来加深对交叉熵的理解。

二、语义分割——MSE  and Cross entropy

2.1什么是MSE

MSE为均方差损失函数，均方差是求一个batch中n个样本的n个输出与期望输出的差的平方的平均值

例如：对于n个样本中有:

  

 2.2.什么是熵，交叉熵，也即Cross entropy

2.2.1.什么是熵？

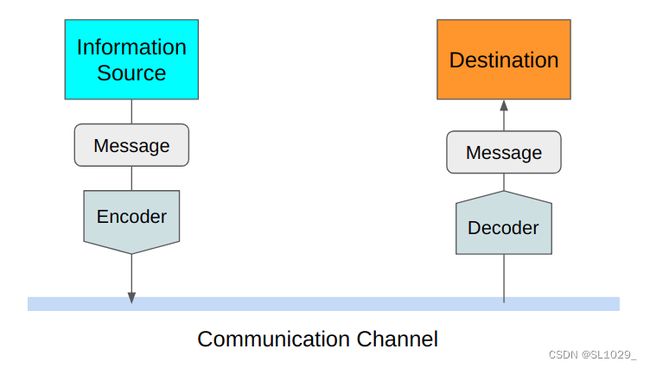
       熵代表着混乱程度、不确定性、不可预测性、信息量。熵是由香农在考虑无损信息编码时提出，目的是为了寻找一种既高效又无损的信息编码方式，简单来说熵就是：无损编码事件信息的最小平均编码长度。

2.2.2.什么是最小无损平均编码长度？

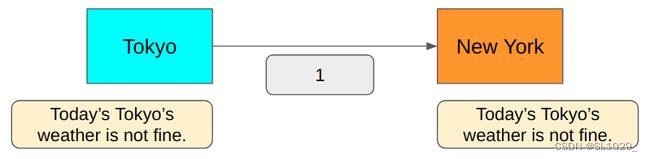
       我们先来看编码怎么是怎么传递信息的，假设我们要传递东京的天气信息好坏给纽约，我们可以打一段话直接告诉纽约那边这边天气很好或者不好，但是这样一段话编码的信息是很长的，事实上我们也没有必要打一大段话来传递信息，因为对于双方来说都知道传递的信息是关于东京的天气的。这样看来我们可以直接用好/不好来传递，这样似乎也不是最短的，再进一步缩减我们可以用Y/N来传递天气好坏，但好像已经很简单了，都只用了一个字母，然而字母本质还是0/1编码来传递的，还是不够短。最后不难想到我们想要传递东京的天气好坏直接用0/1这两个数字就足够传递信息了，因此对于这个例子最小平均编码长度事实上为(1 + 1)/2 = 1。

上面的例子是只传递两种天气，那对于更多的天气该怎么编码呢，例如我们要同时传递fine/snow/cloudy/Rainy四种信息该怎么编码呢，一个比特0/1只能传递两种信息，对于四种信息,不难想到两个比特恰好可以传递四种信息，编码可以为00/01/10/11，平均编码长度为（2 +2 +2 +2 )/ 4 = 2 ，但这是当我们要传递的四种天气信息概率相等得到的，对于天气概率不相等的情况下，这么编码还是不是最小的。例如，假设我们要传递的天气概率分别为下表：

fine	snow	cloudy	rainy
50%	12.5%	25%	12.5%

假设我们依旧使用上面的编码方式00/01/10/11，这样得到的平均编码长度为0.5 * 2 + 0.25 * 2 + 0.125 * 2 + 0.125 * 2 = 2，但是这样并不是最短的平均编码长度。

而如果我们使用0来代表fine,10代表cloudy,111代表snow,110代表rainy,这样编码没有歧义，也没有多余的编码，因此这样的平均编码长度为：0.5 * 1 + 0.25 * 2 + 0.125 * 3 + 0.125 * 3 = 1.75 < 2可以看到这样的编码方式优于2位比特的编码方式。

2.2.3.那么在已知事件概率分布的情况下，如何编码才能得到最短平均编码长度呢，也就是如何才能得到熵？

假设我们有八种信息需要传递，他们的概率都为1/8，不难想到最短编码长度的方式就是使用3个比特来传递信息分别为：000/001/010/011/100/101/110/111，那熵（平均最小编码长度）计算则为3 * 0.125 * 8 = 3

推广到更普遍的情况如果我们要传递n种信息，则需要log(N)数目的比特来编码，然后概率都为1/N = P,这样计算熵有：

 

这就是熵的计算公式的由来，我们回过头来看前面传递四种天气的例子，熵事实上是这样得到的：Entropy = -( log(0.5) * 0.5 + log(0.25) * 0.25 + log(0.125) * 0.125 + log(0.125) * 0.125) = 1.75，这也是这个例子的最短编码长度。

因此我们得到了求最小编码长度也即熵得方法，只需要知道事件的概率分布,由公式：

则可以计算得到，而仔细看这个公式为什么可以得到最小编码长度：主要还是它把概率大的信息用更短的编码来表示，不难证明得到的就是最小的平均编码长度，主要还是基于贪心算法，与哈夫曼编码很相似。

2.2.4怎么理解熵可以代表混乱度、不确定性，信息量呢？

可以这样理解：对于同样的一个事件，概率分布的不同，熵也就不同，熵越大，代表事件概率分布的越平均，这样不确定性就增大了，混乱度也增大了，我们就很难对其准确预测，例如天气分布如果为7/8， 1/24， 1/24， 1/24以及1/4，1/4，1/4，1/4这样我们可以计算熵：前者为-(log(7/8) * 7/8 + 3 * log(1/24) * 1/24) = 0.74, 后者为2，可以看到熵越大分布更平均，也就预测的结果不确定性更大。

而信息量可以这样理解，当一个概率更低的事件发生时，它可以帮我们排除掉更多的可能性，信息熵是用来衡量事物的不确定性的，信息熵越大，则不确定性越大。

2.2.5.那什么是交叉熵？

交叉熵是用来评估当前训练得到的概率分布与真实分布的差异情况。 它刻画的是实际输出（概率）与期望输出（概率）的距离，也就是交叉熵的值越小，两个概率分布就越接近。

熵的计算是在给定概率分布得到的，但是很多时候交叉熵是用在机器学习里面的loss,这时我们并不知道概率分布，但是我们可以得到预测的概率分布来估计熵，由此引出了交叉熵的概念，我们可以假设Q为预测的概率分布，则估计熵为

但是Q是预测的概率分布，这可能与实际的概率分布P偏差很远，这就达不到我们用这个来估计的目的了，在使用交叉熵作为loss时，我们可以使用真实的观测概率分布P也即真实值与对应的预测概率Q预测值来计算，这样才能在训练的时候来拟合概率分布，因此就有了交叉熵公式：

因为熵是最小的理论编码长度，因此交叉熵是大于等于熵

2.2.6.为什么可以交叉熵可以作为训练的损失函数？

在训练时，我们往往会把输出转换为one-hot编码，例如可以有一个三分类的真实标签如下，有两个预测分布分别为Q1 = [0.9， 0.05， 0.05]和Q2[0.4, 0.3, 0.3]则可以分别得到交叉熵为cross entropy1 = -1 * log 0.9 = 0.15而cross entropy2 = -1 * log0.4 = 1.32,可以看到第二个交叉熵远远大于第一个，可见预测结果分布越准确，交叉熵越小，因此交叉熵可以作为损失函数。

cat	dog	pig
[1, 0, 0]	[0, 1, 0]	[0, 0, 1]

强烈建议看看参考博客里面这两篇文章，结合起来看写的很透彻！

Entropy Demystified. Is it a disorder, uncertainty or… | by Naoki | Medium

一文搞懂熵(Entropy),交叉熵(Cross-Entropy) - 知乎 (zhihu.com)

 2.3语义分割使用交叉熵作为损失函数的原因

2.3.1交叉熵权重更新更快

交叉熵往往都是用来替代均方差MSE与sigmoid的组合，对于二分类的损失函数又有

sigmoid损失函数:

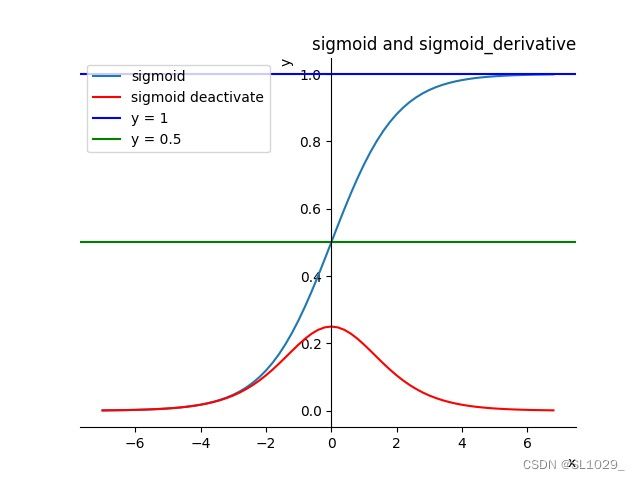
有其图像及其导数图像如下：

画图代码：

import matplotlib.pyplot as plt

import numpy as np

def sigmoid(x):

    y = 1.0/(1 + np.exp(-x))

    return y

def show_sigmoid_and_sigmoid_derivative(x, y1, y2):

    plt.plot(x, y1, label = "sigmoid")

    plt.plot(x, y2, color = "red", label = "sigmoid deactivate")

    plt.axhline(1, color = 'blue', label = "y = 1")

    plt.axhline(0.5, color = "green", label = "y = 0.5")

    plt.legend(loc = "best")

    plt.title("sigmoid and sigmoid_derivative", loc="right")

    plt.xlabel("x", loc='right')

    plt.ylabel("y", loc='top')

    ax = plt.gca() # 获得当前轴

    ax.spines['left'].set_position(('data', 0))

    ax.spines['right'].set_color("None")

    ax.spines['top'].set_color("None")

    plt.savefig("sigmoid.jpg")

    plt.show()

   

def sigmoid_derivative(x):

    y = np.exp(-x) / np.power((1 + np.exp(-x)), 2)

    return y



if __name__ =='__main__':

    x = np.arange(-7, 7, 0.2)

    y1 = sigmoid(x)

    y2 = sigmoid_derivative(x)

    show_sigmoid_and_sigmoid_derivative(x, y1, y2)

   

对于sigmoid函数，x越大或者越小，导数趋于0

对于单个样本，我们可以这样假设：

其中前两步为前向传播，后面L1为均方差损失，L2为交叉熵损失，w,b为权重，σ为激活函数sigmoid,对于权重更新有：

对于均方差损失的偏导数有：

分析：在z很大或者很小的区间，预测值接近1，两个偏导数都比较小，这样会导致参数更新比较慢，收敛自然就变慢了

同时当真实值为1的时候，预测值为1和0导数都为0，真实值为0的时候，预测值为1和0导数也为0，理论上在梯度下降会采取缩小学习率的方式来减小步长，但是在梯度很小的时候，网络并不知道这时候离真实值远还是近，所以这也是不采用MSE的原因

对于交叉熵的偏导数有：

分析：这时候梯度主要受预测值与真实值的差来决定，差越大梯度越大，参数更新越快，差越小，梯度越小参数更新更慢

四、交叉熵的计算

对于图像分割一个训练集，我们需要寻找参数w ̂使得Loss最小，也即

N为训练集图片数量，(), ()为图片与真实值的配对,代表第几张图片，对于每一张图片的Loss有

其中为每张图所有像素构成的空间，i指每一个像素，代表该位置上j类别的真实值，k表示分割的k个类别。

为在该像素位置上j类别的的预测概率

()为该像素位置上激活函数输出的值，一般情况下，我们都需要对激活函数的输出做softmax处理来使预测值在[0,1]之间，所以P其实就是对应类别的可能性。

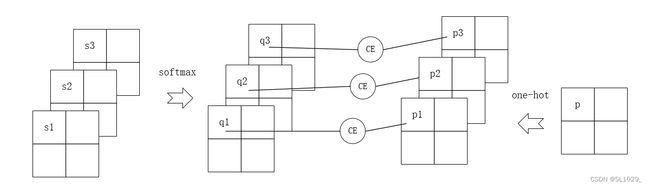
4.1多通道交叉熵的计算

如图为1个三通道的交叉熵的计算，对于输出的每个像素上的值，我们先计算softmax值，得到对应的每个类别的概率，与标签的onehot编码进行计算得到交叉熵

参考博客

语义分割单通道和多通道输出交叉熵损失函数的计算问题 - GShang - 博客园 (cnblogs.com)

【超详细公式推导】关于交叉熵损失函数（Cross-entropy）和 平方损失（MSE）的区别 - 知乎 (zhihu.com)

最详细的语义分割---07交叉熵到底在干什么？_语义分割交叉熵损失函数怎么算_正在学习的浅语的博客-CSDN博客

Entropy Demystified. Is it a disorder, uncertainty or… | by Naoki | Medium

一文搞懂熵(Entropy),交叉熵(Cross-Entropy) - 知乎 (zhihu.com)

为什么用交叉熵做损失函数 - 知乎 (zhihu.com)