【学习笔记】unity脚本学习（三）（向量 Vector3）

新的一周，开启新的学习，加油

向量复习

视频讲得笼统了，还是去复习下高中知识吧

高中向量基础

高中数学平面向量

【数学】向量的四则运算、点积、叉积、正交基

叉乘公式

向量点乘（内积）和叉乘（外积、向量积）概念及几何意义解读
两个向量的叉乘，又叫向量积、外积、叉积，叉乘的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。
对于向量a和向量b：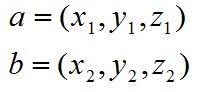
a和b的叉乘公式为：

其中：
根据i、j、k间关系，有：

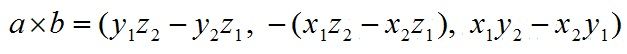
叉乘运算定理

向量外积的高中数学运用

向量、坐标系

• 向量、标量
  标量就是向量的模（取平方根）
• 右手坐标系、左手坐标系
  
  unity用的是左手坐标系

点积

unity提供点积函数 Vector3.Dot(VectorA,VectorB)
点积的应用：

比如用游戏中飞机的forward和世界坐标up进行点积，为0也就是垂直，那么就给它最小的空气阻力，否则加大空气阻力。

叉积

数学上方向用右手螺旋来判断：

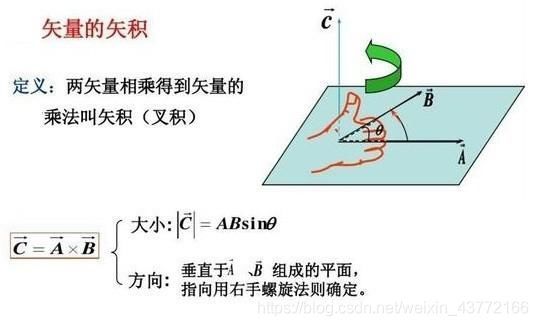
unity中用左手来判断？这点再继续搜查一下！

unity中叉积函数Vector3.Cross(VectorA,VectorB)

应用：

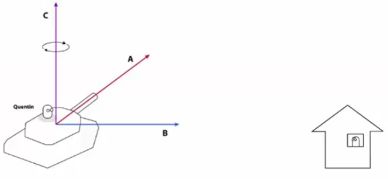
如上：坦克原先朝向A，想在想瞄准B方向，那么就可以A^B，得到垂直的C向量，对C轴进行旋转就能方便地操作物体

Vector3 三维向量

官网Vector3API

静态变量

变量

• magnitude 返回该向量的长度。（只读）
• normalized 返回 magnitude 为 1 时的该向量。（只读）
• sqrMagnitude 返回该向量的平方长度。（只读）
• this[int] 分别使用 [0]、[1]、[2] 访问 x、y、z 分量。

变量normalized 与 Normalize() 方法

normalized 返回 magnitude 为 1 时的该向量。（只读）

进行标准化时，向量方向保持不变，但其长度为 1.0。
请注意，当前向量保持不变，返回一个新的归一化向量。如果 要归一化当前向量，请使用 Normalize 函数。
如果向量太小而无法标准化，则返回零向量。

Normalize 使该向量的 magnitude 为 1。
请注意，此函数将更改当前向量。如果 要保持当前向量不变，请使用 normalized 变量。
如果该向量太小而无法标准化，则将其设置为零。

Vector3 v1;
    Vector3 v2;
    // Start is called before the first frame update
    private void Awake() {
        v1 = transform.position;
    }
    void Start()
    {
        v2 = v1.normalized;
        // v2 = Vector3.Normalize(v1);
        // v1.Normalize();
        Debug.Log("the value of v1:"+ v1.ToString() + " and v1 Magnitude:"+ v1.magnitude.ToString());
        Debug.Log("the value of v2:"+ v2.ToString() + " and v2 Magnitude:"+ v2.magnitude.ToString());
    }

v2 = v1.normalized;执行结果

v2 = Vector3.Normalize(v1);执行结果

v1.Normalize();执行结果

可以看到，只有v1.Normalize()才会对向量本身产生影响，Vector3.Normalize(v1)和 v1.normalized都会生成新的向量。

静态方法

ClampMagnitude

public static Vector3 ClampMagnitude (Vector3 vector, float maxLength);
返回 vector 的副本，其大小被限制为 maxLength。

    public float radius = 1;
    Vector3 v;
    // Update is called once per frame
    void Update()
    {
        transform.position = Vector3.ClampMagnitude(transform.position, radius);   
    }
    private void OnGUI() {
        v = transform.position;
        GUILayout.TextArea("vector:"+ v.ToString() +" ClampMagnitude:" + v.magnitude.ToString());
    }

可以看到物体被限制在1的范围内（原点为中心，1为半径活动）

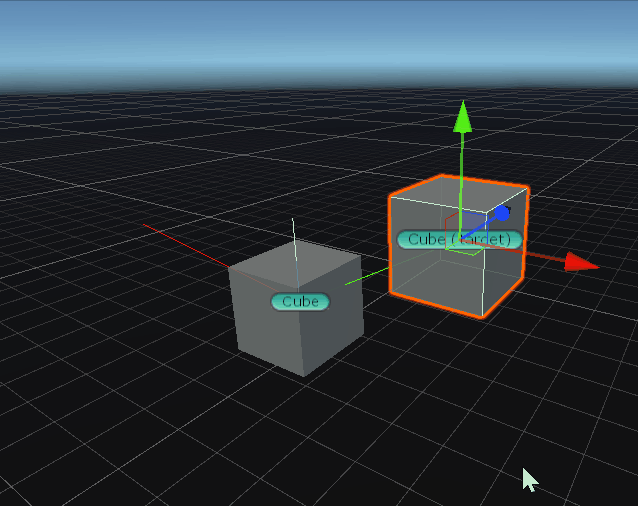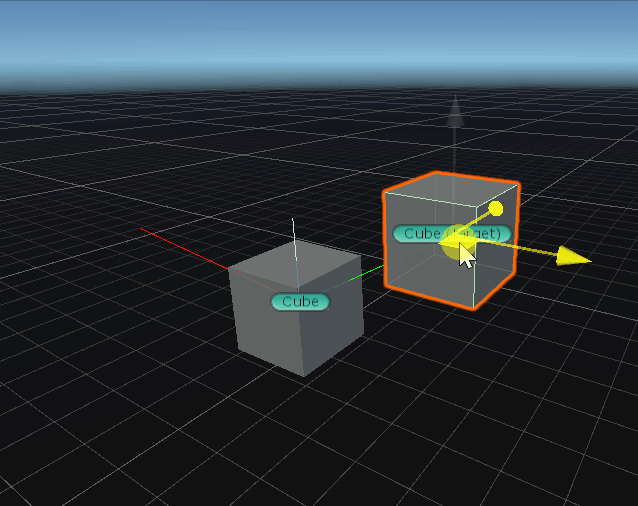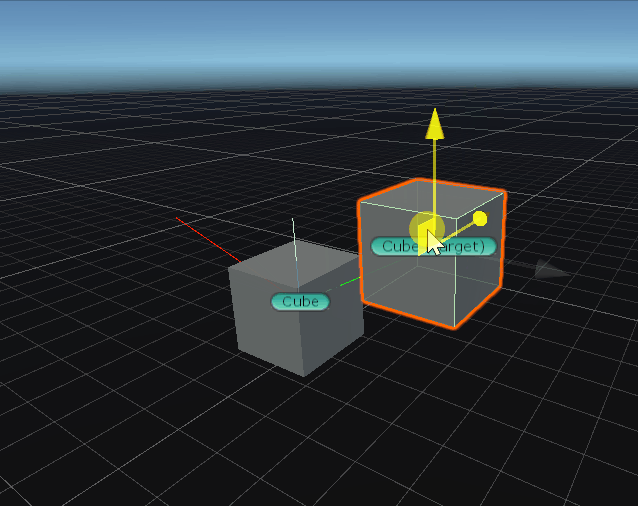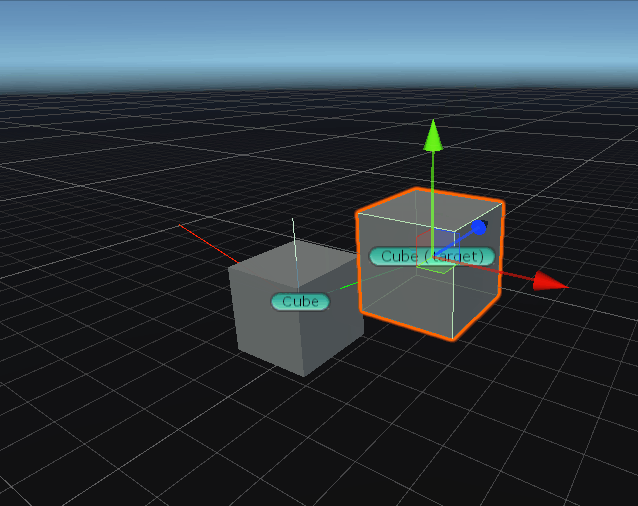
Cross

public static Vector3 Cross (Vector3 lhs, Vector3 rhs);
两个向量的叉积。
两个向量的叉积生成第三个向量， 该向量垂直于两个输入向量。结果的大小等于： 将两个输入的大小相乘，然后乘以输入之间角度的正弦值，即|a||b|sinθ。 可以使用“左手规则”确定结果向量的方向。

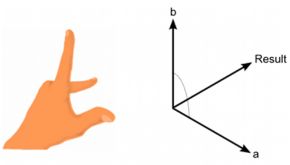
   Vector3 cross;

    // Update is called once per frame
    void Update()
    {
        cross = Vector3.Cross(transform.position,Vector3.up);
        Debug.DrawLine(Vector3.zero ,transform.position, Color.blue);
        Debug.DrawLine(Vector3.zero ,Vector3.up, Color.green);
        Debug.DrawLine(Vector3.zero ,cross, Color.red);
    }

Distance

public static float Distance (Vector3 a, Vector3 b);
返回 a 与 b 之间的距离。

Vector3.Distance(a,b) 与 (a-b).magnitude 相同。

【注意理解：向量表示的是大小和方向，与位置无关】

Dot

public static float Dot (Vector3 lhs, Vector3 rhs);
两个向量的点积。

点积是一个浮点值，它等于 将两个向量的大小相乘，然后乘以向量之间角度的余弦值。
对于 normalized 向量，如果它们指向完全相同的方向，Dot 返回 1； 如果它们指向完全相反的方向，返回 -1；如果向量彼此垂直，则 Dot 返回 0。

MoveTowards

public static Vector3 MoveTowards (Vector3 current, Vector3 target, float maxDistanceDelta);
计算 current 指定的点与 target 指定的点之间的位置，移动距离不超过 maxDistanceDelta 指定的距离。

        // Move our position a step closer to the target.
        var step =  speed * Time.deltaTime; // calculate distance to move
        transform.position = Vector3.MoveTowards(transform.position, target.position, step);

【这里我原来比较难以理解的是，向量不应该是与位置无关的吗，为什么还能标定起始点还有移动这种概念。我自己理解了下，这个Vector3 的moveTowards 实际上就是沿着（target - current）方向进行移动，移动大小不超过|target - current|和maxDistanceDelta，所以说还是向量的方向和大小的概念，所谓的位置改变针对的是position而已，更像是对物体施加一个力，力只有方向和大小，与位置无关，只是这个力使物体产生了位移了罢】

其他变换类似

Lerp 在两个点之间进行线性插值。

RotateTowards 将向量 current 朝 target 旋转。

Slerp 在两个向量之间进行球形插值。

SmoothDamp 随时间推移将一个向量逐渐改变为所需目标。

Max

public static Vector3 Max (Vector3 lhs, Vector3 rhs);
返回由两个向量的最大分量组成的向量。

 // prints (4.0f, 3.0f, 3.0f)
print(Vector3.Max(new Vector3(1, 2, 3), new Vector3(4, 3, 2)));

Min

返回由两个向量的最小分量组成的向量。

Scale

将两个向量的分量相乘。

// This will compute Vector3(2, 6, 12)
print(Vector3.Scale(new Vector3(1, 2, 3), new Vector3(2, 3, 4)));

---

下面是比较不好理解的几个

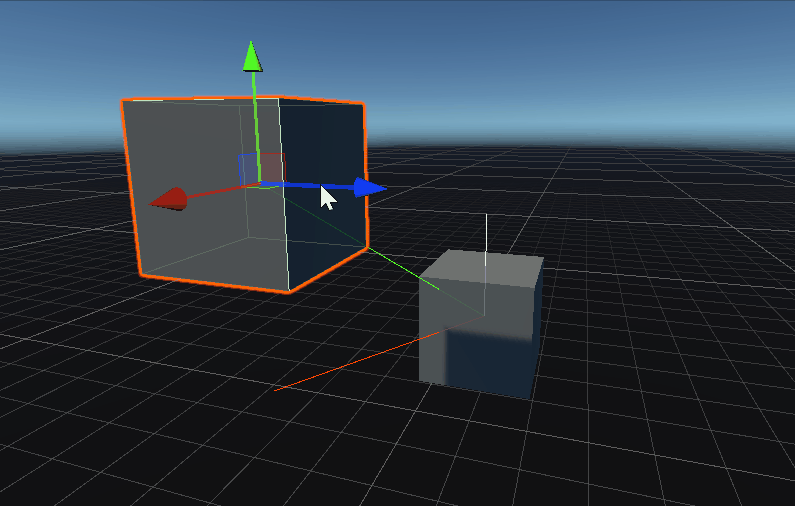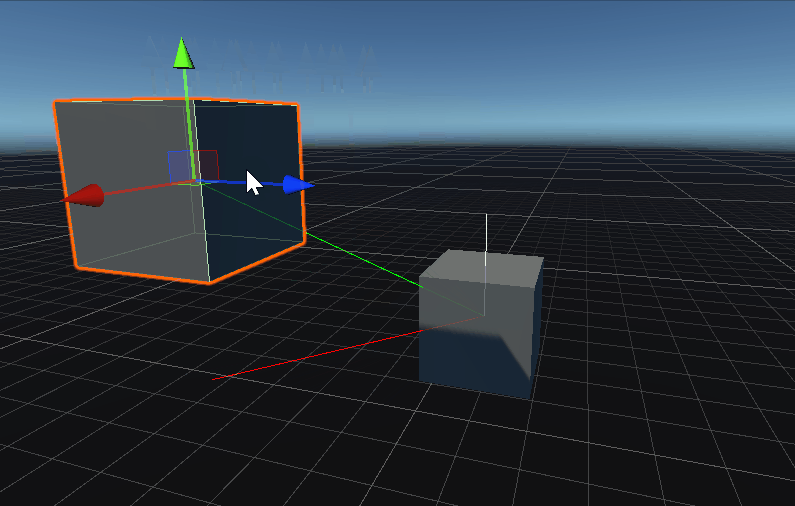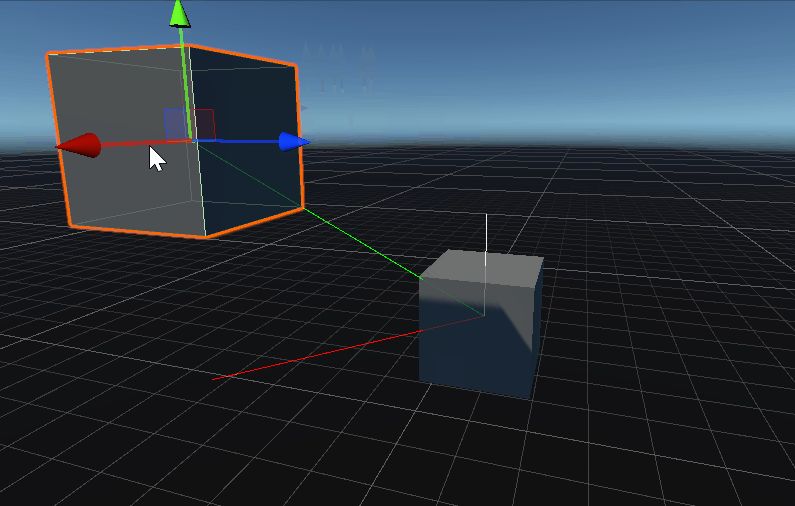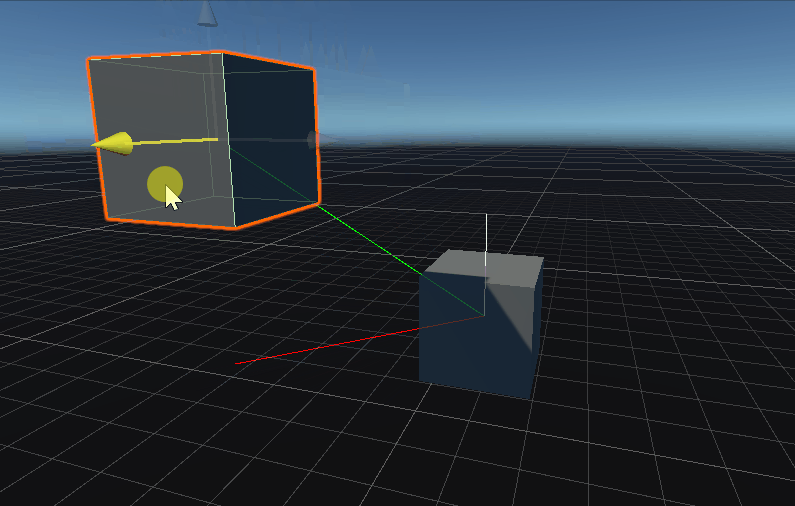
OrthoNormalize 将向量标准化并使它们彼此正交。

public static void OrthoNormalize (ref Vector3 normal, ref Vector3 tangent);
public static void OrthoNormalize (ref Vector3 normal, ref Vector3 tangent, ref Vector3 binormal);
将向量标准化并使它们彼此正交。
标准化 tangent。 标准化 tangent 并确保其与 normal 正交（即它们之间的角度为 90 度）。

    public Transform obj1;
    public Transform obj2;
    Vector3 a,b,c,d,e,f;

    // Update is called once per frame
    void Update()
    {
        a =transform.position;
        b = obj1.position;
        c = obj2.position;
        d = a;
        e = b;
        f = c;
        Vector3.OrthoNormalize(ref a, ref b, ref c);
        Debug.DrawLine(Vector3.zero,d,Color.yellow);
        Debug.DrawLine(Vector3.zero,e,Color.white);
        Debug.DrawLine(Vector3.zero,f,Color.black);
        Debug.DrawLine(Vector3.zero,a,Color.red);
        // 注：绿色切线我延长了，方便观察
        Debug.DrawLine(Vector3.zero,b*10,Color.green);
        Debug.DrawLine(Vector3.zero,c,Color.blue);
        Debug.DrawLine(d,e,Color.grey);
    }

从图中可以看到，生成的切线、次法线只与第一和第二个参数有关，所以提供了一个两个参数的函数。
其中生成的切线（绿色）与 向量a和向量b同平面，且垂直于向量a，生成的次法线（蓝线）垂直于法线（红线）与切线（绿线）。

Project 将向量投影到另一个向量上。

public static Vector3 Project (Vector3 vector, Vector3 onNormal);

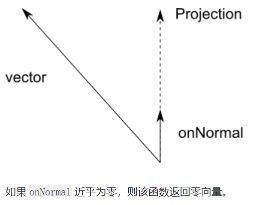
    public Transform target;
    public Vector3 rail;
    private void Update() {
        Vector3 heading = target.position-transform.position;
        Vector3 project = Vector3.Project(heading,rail);
        Debug.DrawLine(transform.position,target.position,Color.green);
        Debug.DrawLine(transform.position,transform.position + project,Color.red);
    }

ProjectOnPlane 将向量投影到由法线定义的平面上（法线与该平面正交）。

public static Vector3 ProjectOnPlane (Vector3 vector, Vector3 planeNormal);
两个投影和数学概念一致

public Transform target;
    public Vector3 rail;
    private void Update() {
        Vector3 heading = target.position-transform.position;
        Vector3 project = Vector3.ProjectOnPlane(heading,rail);
        Debug.DrawLine(transform.position,target.position,Color.green);
        Debug.DrawLine(transform.position,transform.position + project,Color.red);
        Debug.DrawLine(transform.position,transform.position+rail,Color.white);        
    }

Reflect 从法线定义的平面反射一个向量。

public static Vector3 Reflect (Vector3 inDirection, Vector3 inNormal);

public Transform target;
    public Vector3 rail;
    private void Update() {
        Vector3 heading = transform.position-target.position;
        Vector3 reflect = Vector3.Reflect(heading,rail);
        Debug.DrawLine(transform.position,target.position,Color.green);
        Debug.DrawLine(transform.position,transform.position + reflect,Color.red);   
        Debug.DrawLine(Vector3.zero +transform.position,transform.position + rail,Color.white);    
    }

结言

ok，花了两天终于把Vector搞完了，内容也挺多的，之前transform没懂的部分在这块也补充了。
加油！继续输入输出~