贪心算法（几种常规样例）

贪心算法（几种常规样例）

贪心算法，指在对问题进行求解的时候，总是做出当前看来是最好的选择。也就是说不从整体上最优上考虑，算法得到的结果是某种意义上的局部最优解

---

介绍

可以用贪心算法解决的问题有以下特征

• 1.贪心选择的性质：一个问题的整体最优解可以通过一系列局部的最优解的选择达到。并且每一次的选择可以依赖于之前做出的选择，但是不依赖后面做出的选择。这就是贪心选择性质。对于一个具体的问题，要确定他是否具有贪心选择的性质，必须证明每一步所作的贪心选择最终导致问题的整体的最优解

• 2.最优子结构性质：当一个恩问题的最优解包含其子问题的最优解的时候，此问题具有最优子结构性质。问题的最优子结构性质是该问题可用贪心法的求解所在。

使用步骤

使用贪心算法的基本步骤：
   1>建立数学模型来描述问题 。
   2>把求解的问题分成若干个子问题 。
   3>对每个子问题求解，得到子问题的局部最优解。
   4>把子问题的解局部最优解合成原来解问题的一个解。

实际上在使用贪心算法的时候，待选

模板

while(约束条件成立)
{
    选择当前最优解，记录并累计到最后的解中
        if(当前最优解使用完毕)
    	当前最优解=当前次优解；
}

贪心算法的缺陷

​ 以下缺陷

​ 1.不能保证解是最佳的。因为贪心算法得到的是局部最优解，不是从整体开了整体最优解。

​ 2.贪心算法只能确定某些问题的可行性范围

缺陷1和2的意思是贪心算法是有局限性的，就i比如钱币找零，如果是8元，有2元和5元，那么5元一张，2元一张，剩下1元那么接下来就无法运算了，实际上，可以四张2元即可，这就是一个例子

​ 3.贪心算法一般用来解决最大或者最小解

该缺陷就是，贪心算法是以某一种策略来选择一个数值，而不是遍历出所有解，要遍历出某个问题的所有解的话，常常使用回溯法

经典例子

1.活动选择问题

2.钱币找零问题

3.再论背包问题

4.小船过河问题

5.区间覆盖问题

常见例子

活动选择问题

该问题一般可以用贪心算法和动态规划来解决，我们下文用贪心算法来解决。
问题的形式为：在某地要举办多个活动，每一个活动要花费不同的时间（起止时间不同），问怎么安排尽量多的活动呢？该问题用贪心算法可以解决的原因是：下个活动的选择可以只是取决于上一个活动的截止时间，不必要考虑全局

活动	1	2	3	4	5	6	7	8	9	10	11
开始时间	1	3	0	5	3	5	6	8	8	2	12
结束时间	4	5	6	7	8	9	10	11	12	13	14

在解决这个问题的时候，要对于结束时间进行排序，因为上一个活动的结束时间会影响下一个活动的选择，而当前活动的开始时间不会影响下一个活动的选择，所以只看结束时间就好，用上一个活动的结束时间来跟下一活动的开始时间进行对比，如果前者小于后者，那么就是后者就是下一个活动，否则继续比较下下一个活动的开始时间

解题思路

1. 将所有活动按照结束时间进行排序
2. 然后默认选取第一个活动，用变量endTime标注当前活动的结束时间，然后与后面活动的开始时间进行比较
3. 如果前者结束时间小于等于后者活动开始时间，那么选择后者这个活动，反之，继续比较下下一个活动，再次进行判断
4. 重复进行第三步，直到所有活动比较完成

import java.util.*;

/**
 * 活动选择：
 * 大概形式为：在某一个地方，有多个活动要进行，活动有开始时间和结束时间，我们该如何选择才能在这一天中这一个地点，举办最多的活动
 * 求解最多的活动个数为？
 */
class Play{
    int preTime;
    int endTime;//表示活动的开始时间和结束时间
}
public class 活动选择 {
    public static void main(String[] args) {
        Scanner scanner=new Scanner(System.in);
        //我们可以用容器来存储各个活动，然后进行贪心算法，最后得到结果
        //我们可以用链表来进行存储,排序
        LinkedList<Play> linkedList=new LinkedList();
        int n=scanner.nextInt();//表示活动的个数
        for (int i = 0; i <n ; i++) {
            //提案写每一个活动的开始时间和结束时间
            Play play=new Play();
            play.preTime=scanner.nextInt();
            play.endTime=scanner.nextInt();
            linkedList.add(play);//存储链表中，然后进行对于结束时间排序
        }
        Collections.sort(linkedList, new Comparator<Play>() {
            @Override
            public int compare(Play o1, Play o2) {
                return o1.endTime-o2.endTime;
            }
        });
        //排序完成
        //然后进行判别，从第一个活动开始
        int num=0;//计数
        Play Time=linkedList.get(0);
        for (int i = 0; i <linkedList.size() ; i++) {
            if(Time.endTime<=linkedList.get(i).preTime){
                Time=linkedList.get(i);
                num++;
            }
        }
        System.out.println(num);//得到
    }
}

钱币找零问题

该问题的一般描述是：假设1元、2元、5元、10元、20元、50元、100元的纸币分别有a , b , c , d , e ,f 张。现在要用这些钱来支付K元，至少要用多少张纸币？该问题和上个问题有些类似，要解决该问题时，一般也有两个数组，一个表示面额的大小，一个表示不同面额钱币对应的数量，并且表示面额的数组是有序的。

我们求解的是最少的钱币数目，所以可以使用贪心算法

1.理所当然先使用大额纸币，当大额纸币张数不够的时候，再使用后面较小面额的纸币，依次递减，直到表示完所有纸币

2.做题方法可以递归也可以迭代

import java.util.*;

public class 钱币找零问题 {
    public static void main(String[] args) {
        //题目：指定币值和相应的数量，用最少的数量去凑齐某金额
        //思路：利用贪心算法，我们优先选择面值大的纸币，依次类推，直到凑齐总金额
        Scanner scanner=new Scanner(System.in);
        int num=scanner.nextInt();//输入总金额
        greedy(num);
    }
    public static void greedy(int num){
        int[] values = { 1, 2, 5, 10, 20, 50, 100 };
        //数量
        int[] counts = { 3, 3, 2, 1, 1, 3, 3 };
        //获取需要各种面值多少张
        int[] result = getNumber(num, values, counts);
        System.out.println("各币值的数量："+Arrays.toString(result));
    }
    public static int[] getNumber(int sum,int []values,int[]counts){
        int []result=new int[7];//表示有七种钱币
        //我们要找的是每一种钱币所需的票数
        int add=0;//表示需要的总钱数
        for (int i = values.length-1; i >=0 ; i--) {
            int num=(sum-add)/values[i];
            if(num>counts[i]){
                num=counts[i];
            }
            //add加上数值
            add=add+num*values[i];
            result[i]=num;
        }
        return result;
    }
    //或者这样迭代
    public static int[] get(int sum,int []values,int[]counts){
        int []result=new int[values.length];
        for (int i = values.length-1; i >=0 ; i++) {
            int num=Math.min(counts[i],sum/values[i]);
            result[i]=num;
            sum=sum-num*values[i];
        }
        return result;
    }
}

背包问题

不是01背包

常见题型为给定n种物品，一个背包，背包的容量是c，二米一个物品i的价值为vi，重量为wi，如何选择装入的物品使得背包的总价值最大？

此处的背包问题指的是部分背包，不是像01背包问题那样，某个物品不能拆开，此处的物品可以拆开，选取一部分放入背包中。从贪心算法的角度来看，我们保证的是背包的总价值最大，就是要确保放入的每一件物品的单个价值尽量大。（可以拆开）

步骤如下

1.需要将物品按照单位重量价值进行排序。

2.将尽可能多的单位i重量价值最高的物品装入被阿波，若最大单位重量价值的物品全部装入背包后，背包华友多余容量，则选择单位重量价值次高的尽可能多的装入背包中。

3.如果最后一件物品无法装入，那就计算可以装入的比例，然后按照比例装入

import java.util.Collections;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.Scanner;

/**
 * 贪心的背包 ，有n个物品，一个背包，然后想使得这个背包的价值最大
 * 不是01背包不可拆分物品，这个是可以拆分的
 */
class beiBao{
    int values;
    int weight;//价值和重量
    double wValues;//单个物品的单位重量的价值
}
public class 背包 {

    public static void main(String[] args) {
        Scanner scanner=new Scanner(System.in);
        int n=scanner.nextInt();
        int weight=scanner.nextInt();//背包能承受的重量
        LinkedList<beiBao> linkedList=new LinkedList();
        for (int i = 0; i <n ; i++) {
            beiBao b=new beiBao();
            b.values=scanner.nextInt();
            b.weight=scanner.nextInt();
            b.wValues=b.values/b.weight;
            linkedList.add(b);
        }
      Collections.sort(linkedList, new Comparator<beiBao>() {
          @Override
          public int compare(beiBao o1, beiBao o2) {
              return (int)(o2.wValues-o1.wValues);
          }
      });
        for (int i = 0; i <n ; i++) {
            System.out.println(linkedList.get(i).wValues);
        }
        double allvalues=0;
        boolean[] flag=new boolean[n];
        for (int i = 0; i < flag.length; i++) {
            flag[i]=false;//表示没有放入背包中
        }
        for (int i = 0; i <n ; i++) {
            if(linkedList.get(i).weight<=weight){
                flag[i]=true;
                weight=weight-linkedList.get(i).weight;
                allvalues+=linkedList.get(i).values;
                System.out.println("重量为："+linkedList.get(i).weight+"价格为："+linkedList.get(i).values+"可以完全装入");
            }
        }
        for (int i = 0; i <n ; i++) {
            if(!flag[i]){
                double rate=(double)weight/linkedList.get(i).weight;
                allvalues=allvalues+rate*linkedList.get(i).values;
                weight-=linkedList.get(i).weight;
                System.out.println("重量为："+linkedList.get(i).weight+"价值为："+linkedList.get(i).values+"装入比例为："+rate);
            }
        }
        System.out.println("总价值为："+allvalues);
    }
}

小船过河问题

该问题常见的描述是：有n个人需要过河，只有一艘船，最多能乘坐两个人，串的航行速度为两人中较慢的一人的速度，过去后需要一个人把船划回来，把n个人运到对岸，最少需要多久。

假设这些人花费的时间都存储在一个数组中，升序排列，也就是由快到慢，每个人所花费的时间为time[0],time[1]……time[n]

当人数>=4的时候，该问题有两个选择：
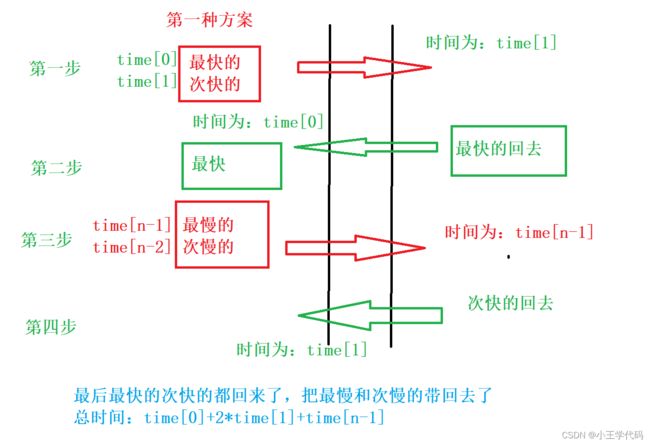
1.最快的和次快的先过河，然后最快的将船划回来；次慢的和最慢的过河，然后次快的回来，此时我们计算以下这个过程花费的时间

图示

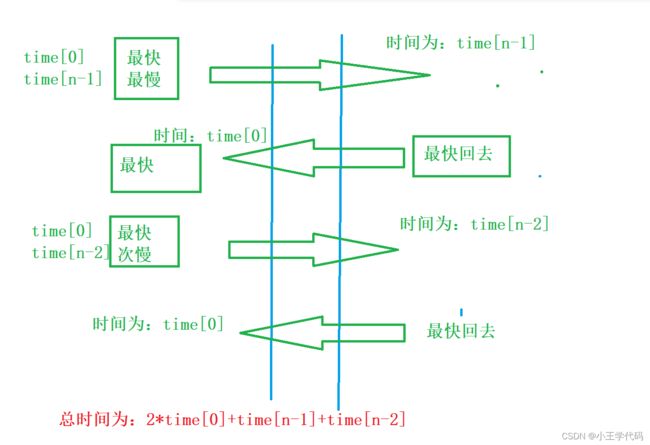
第二种方式：

​ 1.最快的最慢的过河，然后最快的将船划回来，，最快的和次慢的过河，然后最快的再回来

图示

上面过河有两种方式，具体使用的时候可以比较谁时间更短再使用他

如果人数小于4

1.人数为三的时候，此时固定用时为time[0]+time[1]+time[2]

2.人数为二的时候，此时固定用时为time[1]

3.人数为一的时候，固定用时为time[0]

/*
 * 有n个人需要过河，只有一艘船，最多能乘2人，船的运行速度为2人中较慢一人的速度，
 * 过去后还需一个人把船划回来，把n个人运到对岸，最少需要多久。
 */
public class River {
    public static void main(String[] args) {
    	int[] times={1,2,4,5,8};
    	int result=crossRiver(times);
    	System.out.println("所花时间为："+result);
    }
    
    private static int crossRiver(int[] times){
    	/*n表示还未过河的人数，初始化为所有人*/
    	int n=times.length;
    	int result=0;
    	while(n>0){
    		if(n==1){
    			result=result+times[0];
    			break;
    		}else if(n==2){
    			result=result+times[0]+times[1];
    			break;
    		}else if(n==3){
    			result=result+times[0]+times[1]+times[2];
    			break;
    		}else{
    			/*在每次过河时，在两种方式上进行比较，选择耗时更少的那个*/
    			result=result+Math.min(times[1]+times[0]+times[n-1]+times[1],times[n-1]+times[0]+times[n-2]+times[0]);
    			/*无论采取哪种方式，最后的结果都是讲最慢的和次慢的运送过河，也就是数组的最后两位，所以此处可简单地将数组长度-2*/
    			n=n-2;
    		}
    	}
    	return result;
    }
}

区域覆盖

此问题描述的是：给定一个长度为m的区间，再给出n条线段的起点和终点（闭区间），求最少使用读哦少条线段 可以将整个区间完全覆盖，步骤如下：

1. 在所有待选择的区间里，剔除起点和终点在所求范围之外的区间。
2. 将所有区间按起点进行排序
3. 默认选中第一个点，然后在挑选点的过程中，需要遵循以下原则：新区间的起点要小于当前区间的终点，新区间的终点应大于当前区间的起点
4. 循环重复步骤3，直到当前区间的终点值>=预期的终点值，结束寻找区间的过程

import java.util.*;
class quJian{
    int pre;
    int end;//表示区间的起点和终点
}
public class 区间覆盖 {
    public static void main(String[] args) {
        Scanner scanner=new Scanner(System.in);
        //加入区间 10个
        int n=scanner.nextInt();
        int m=scanner.nextInt();
        //假设所求区间范围为[n,m]；
        LinkedList <quJian>linkedList=new LinkedList();
        for (int i = 0; i <7 ; i++) {
            quJian qj=new quJian();
            qj.pre=scanner.nextInt();
            qj.end=scanner.nextInt(); //1.删除起点和终点在所要求范围外的区间
            if(!(qj.pre<n&&qj.end<n||qj.pre>m&&qj.end>m)){
                linkedList.add(qj);
            }
        }
        //先进行排序
        Collections.sort(linkedList, new Comparator<quJian>() {
            @Override
            public int compare(quJian o1, quJian o2) {
                return o1.pre-o2.pre;//按照小区间的起点排下序，升序
            }
        });
       //然后进行选取
        boolean flag=false;
        int count=1;//计数
        System.out.println("起点："+linkedList.get(0).pre+","+linkedList.get(0).end);
        int end=linkedList.get(0).end;
        for (int i = 1; i <linkedList.size() ; i++) {
            if(linkedList.get(i).pre<=end&&linkedList.get(i).end>end){
                end=linkedList.get(i).end;//更新end点
                for (int j = i+1; j <linkedList.size() ; j++) {
                    //然后从这后面找到最长的end
                    if(linkedList.get(j).end>end){
                        end=linkedList.get(j).end;
                        count++;//找到一个区间
                        System.out.println(linkedList.get(j).pre+" "+linkedList.get(j).end);
                        if(end>=m){
                            flag=true;
                        }
                    }

                }
            }
            if(flag){
                break;
            }
        }
        System.out.println(count);
    }
}