【机器学习】十二、一文看懂支持向量机原理
说明:本文是一篇学习笔记,在看完很多大佬对SVM的讲解之后,自己Copy和整理的,仅供学习使用,码字不易,喜欢请点赞!!!

一、SVM简介
支持向量机,英文名Support Vector Machine,因此简称SVM。SVM是应用最广泛、并且效果很不错分类算法。李航的《统计学习方法》对SVM的原理进行了详细的推导,CSDN的博客专家July也对SVM的数学原理进行了完整的总结。本文在看了这些大佬的文章后,做出了自己的整理,希望供自己日后学习使用,也提供给大家学习参考使用。本文主要包括以下部分:
- 线性可分SVM
- 线性不可分SVM
- SVM公式推导用到的知识简介
- 离群点处理
- 主要参数
二、线性可分情况下的SVM
2.1 线性可分简介
对于二分类问题,如果线性可分的话,你可能首先想到的是逻辑回归,前面我们分享过逻辑回归的原理,知道逻辑回归通过将线性回归的值使用Sigmoid函数映射到区间(0,1)之间,然后根据预测值与0的大小关系对比,来判断y属于哪一类。
 在逻辑回归里面使用的是 θ T x \theta ^Tx θTx来表示分割超平面,其中有:
在逻辑回归里面使用的是 θ T x \theta ^Tx θTx来表示分割超平面,其中有:
θ T x = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n \theta ^Tx=\theta _0+\theta _1x_1+\theta _2x_2+...+\theta _nx_n θTx=θ0+θ1x1+θ2x2+...+θnxn
因此逻辑回归分类的结果,只和 θ T x \theta ^Tx θTx的正负有关,即:
i f if if θ T x > 0 \theta ^Tx>0 θTx>0 t h e n then then y = 1 y=1 y=1 , e l s e else else i f if if θ T x < 0 \theta ^Tx<0 θTx<0 t h e n then then y = 0 y=0 y=0。
这里令 θ 0 = b \theta _0=b θ0=b, θ 1 x 1 + θ 2 x 2 + . . . + θ n x n = w T x \theta _1x_1+\theta _2x_2+...+\theta _nx_n = w^Tx θ1x1+θ2x2+...+θnxn=wTx
则有:
θ T x = w T x + b \theta ^Tx= w^Tx+b θTx=wTx+b
在逻辑回归中,y的值取0和1,这里我们将分类的y的值取-1和1(即将分类标签0使用-1替换)。则有:
i f if if w T x + b > 0 w^Tx+b>0 wTx+b>0 t h e n then then y = 1 y=1 y=1 , e l s e else else i f if if w T x + b < 0 w^Tx+b<0 wTx+b<0 t h e n then then y = − 1 y=-1 y=−1。
并且我们有 y ( w T x + b ) > 0 y(w^Tx + b) >0 y(wTx+b)>0,则分类正确。

所以我们需要找到一个超平面,使得能分开两类数据。那么怎么分开效果更好呢,下图明显课件绿色分割平面由于红色分割平面。那么分开的标准是什么呢?请看下一节。

2.2 函数间隔 and 几何间隔
这部分参考了知乎朋友Jason对函数间隔和集合间隔的解释,参考链接见文末参考文献。
我么知道SVM是通过超平面来讲样本分成两类的,在超平面 w T x + b = 0 w^Tx+b=0 wTx+b=0确定的情况下,那么 ∣ w T x + b ∣ |w^Tx+b| ∣wTx+b∣可以表示点x距离超平面的相对距离,为什么是相对距离呢?一会儿你就知道了。
前面说了, y ( w T x + b ) > 0 y(w^Tx + b) >0 y(wTx+b)>0,则分类正确,否则分类错误。并且有 y ( w T x + b ) y(w^Tx + b) y(wTx+b)的值越大,则分类的可信度越高,反之亦然。
所以样本点 ( x i , y i ) (x_i,y_i) (xi,yi)到超平面 ( w , b ) (w,b) (w,b)的函数间隔定义为:
γ i = y i ( w T x i + b ) \gamma_i=y_i(w^Tx_i + b) γi=yi(wTxi+b)
但是你会发现,如果 w w w和 b b b同比例增大的话,超平面不变,而函数间隔会变大,这也是为什么函数间隔只能给出点到平面的相对距离大小。
几何间隔定义如下:
γ i = y i ( w T x i + b ) ∣ ∣ w ∣ ∣ \gamma_i=\frac{y_i(w^Tx_i + b)}{||w||} γi=∣∣w∣∣yi(wTxi+b)
实际上,几何间隔就是点到超平面的距离。而函数距离就是未归一化的距离。
而训练集到超平面的最小几何间隔即为这些样本到超平面的几何间隔。
2.3 最大间隔分类器
SVM训练分类器的方法是寻找到超平面,使正负样本在超平面的两侧,且样本到超平面的几何间隔最大。

所以SVM可以表述为求解下列优化问题:
max w , b γ \max \limits_{w,b} {\gamma} w,bmaxγ
s . t . y i ( w T x i + b ) ∣ ∣ w ∣ ∣ > = γ s.t. \frac{y_i(w^Tx_i + b)}{||w||}>=\gamma s.t.∣∣w∣∣yi(wTxi+b)>=γ
前面说了函数间隔中 w w w和 b b b同比例增大的话,超平面不变,因此可以令函数间隔为1,即:
y i ( w T x i + b ) = 1 y_i(w^Tx_i + b)=1 yi(wTxi+b)=1
因此几何间隔为: 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1
同时,目标函数变化为:
max w , b 1 ∣ ∣ w ∣ ∣ \max \limits_{w,b} {\frac{1}{||w||}} w,bmax∣∣w∣∣1
s . t . s.t. s.t. y i ( w T x i + b ) > = 1 y_i(w^Tx_i + b)>=1 yi(wTxi+b)>=1

2.4 SVM求解
上面说到,SVM在给定函数间隔为1的情况下,目标函数如下:
max w , b 1 ∣ ∣ w ∣ ∣ \max \limits_{w,b} {\frac{1}{||w||}} w,bmax∣∣w∣∣1
s . t . s.t. s.t. y i ( w T x i + b ) > = 1 , i = 1 , 2 , . . . , n y_i(w^Tx_i + b)>=1 ,i=1,2,... ,n yi(wTxi+b)>=1,i=1,2,...,n
我们知道 max w , b 1 ∣ ∣ w ∣ ∣ \max \limits_{w,b} {\frac{1}{||w||}} w,bmax∣∣w∣∣1 等价于 min w , b 1 2 ∣ ∣ w ∣ ∣ 2 \min \limits_{w,b} {\frac{1}{2}||w||^2} w,bmin21∣∣w∣∣2,因此目标函数可以转换为:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 \min \limits_{w,b} {\frac{1}{2}||w||^2} w,bmin21∣∣w∣∣2
s . t . s.t. s.t. y i ( w T x i + b ) > = 1 , i = 1 , 2 , . . . , n y_i(w^Tx_i + b)>=1 ,i=1,2,... ,n yi(wTxi+b)>=1,i=1,2,...,n
目标函数为二次的,约束条件是线性的,因此是一个凸二次规划问题(对于凸集、凸函数以及凸优化的讲解见第四部分)。
但是这里这个问题可以引入拉格朗日对偶性,然后可以通过求解原始问题的对偶问题来得到原始问题的最优解,这样将会更容易求解。引入拉格朗日乘子 α \alpha α后的拉格朗日函数为:
L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 − ∑ i = 1 n [ α i ( y i ( w T x i + b ) − 1 ) ] L(w,b,\alpha)= {\frac{1}{2}||w||^2} - \sum_{i=1}^{n}[\alpha _i(y_i(w^Tx_i + b)-1)] L(w,b,α)=21∣∣w∣∣2−∑i=1n[αi(yi(wTxi+b)−1)]
然后我们自定义函数 θ ( w ) \theta (w) θ(w),并且令:
θ ( w ) = max α i > = 0 L ( w , b , α ) \theta (w)=\max \limits_{\alpha_i>=0}{L(w,b,\alpha)} θ(w)=αi>=0maxL(w,b,α)
那么,我们可以知道,但某个约束条件不满足,即 y i ( w T x i + b ) < 1 y_i(w^Tx_i + b) < 1 yi(wTxi+b)<1时,则会有 θ ( w ) \theta (w) θ(w)为 ∞ \infty ∞。而当所有约束条件满足的时候,则有
θ ( w ) = 1 2 ∣ ∣ w ∣ ∣ 2 \theta (w)={\frac{1}{2}||w||^2} θ(w)=21∣∣w∣∣2。因此最小化 1 2 ∣ ∣ w ∣ ∣ 2 {\frac{1}{2}||w||^2} 21∣∣w∣∣2,即等价于最小化 θ ( w ) \theta (w) θ(w)。
因此,目标函数等价于:
min w , b θ ( w ) = min w , b max α i > = 0 L ( w , b , α ) = p ∗ \min \limits_{w,b}{\theta (w)}=\min \limits_{w,b}\max \limits_{\alpha_i>=0}{L(w,b,\alpha)}=p^* w,bminθ(w)=w,bminαi>=0maxL(w,b,α)=p∗
这里用 p ∗ p^* p∗表示这个问题的最优值,且和最初的问题是等价的。如果直接求解,那么一上来便得面对w和b两个参数,而 α i \alpha _i αi又是不等式约束,这个求解过程不好做。不妨把最小和最大的位置交换一下,变成:
max α i > = 0 min w , b L ( w , b , α ) = d ∗ \max \limits_{\alpha_i>=0}\min \limits_{w,b}{L(w,b,\alpha)}=d^* αi>=0maxw,bminL(w,b,α)=d∗
交换以后的问题是原问题的对偶问题,并且有 d ∗ < = p ∗ d^*<=p^* d∗<=p∗,在满足某些条件的情况下,这两者相等,这个时候就可以通过求解对偶问题来间接地求解原始问题。
然后求解这个maxmin问题。
(1)首先我们固定 α \alpha α,我们知道求解 min w , b L ( w , b , α ) \min \limits_{w,b}{L(w,b,\alpha)} w,bminL(w,b,α)这个最小值,可以对 L ( w , b , α ) L(w,b,\alpha) L(w,b,α)进行求导,然后令 ∂ L ∂ w \frac{∂L}{∂w} ∂w∂L和 ∂ L ∂ b \frac{∂L}{∂b} ∂b∂L的结果等于0即可。
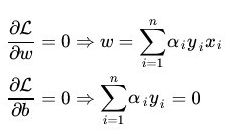
将计算结果带入 L ( w , b , α ) L(w,b,\alpha) L(w,b,α),则有:
 因此有:
因此有:
 (2)然后求对 α \alpha α的极大值。这里的目标函数如下:
(2)然后求对 α \alpha α的极大值。这里的目标函数如下:
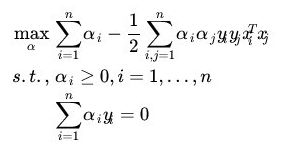
因此只要求出 α \alpha α,就能根据上一步的结果求得 w w w和 b b b的值。从而得到分割的最优超平面。
而这里求解 α \alpha α的值,需要用到SMO算法来求解对偶问题中的拉格朗日乘子 α \alpha α。而想看SMO算法原理的可以参考附件的参考文献。
三、线性不可分SVM
3.1 核函数
从上面的推导我们有: w = ∑ i = 1 n α i y i x i w=\sum_{i=1}^n\alpha _iy_ix_i w=∑i=1nαiyixi,带入超平面得到:
f ( x ) = w T x + b = ( ∑ i = 1 n α i y i x i ) T x + b = ∑ i = 1 n α i y i < x i T , x > + b f(x)=w^Tx+b=(\sum_{i=1}^n\alpha _iy_ix_i)^Tx+b=\sum_{i=1}^n\alpha _iy_i<x_i^T,x>+b f(x)=wTx+b=(∑i=1nαiyixi)Tx+b=∑i=1nαiyi<xiT,x>+b
其中 < x i T , x > + b <x_i^T,x>+b <xiT,x>+b表示的是向量内积。从这里可以看出,新的点 x x x的预测值,只和少量的support vector的内积有关,而对于不是support vector的点,其系数 α = 0 \alpha=0 α=0,因此新点的预测不需要和所有的训练数据进行计算。
到现在的话,我们的SVM只能处理线性可分的情况,而对于如下图的情况,我们就需要引入核函数来处理。

核函数可以将低维数据映射到高维空间,然后在高维空间中,得到分离超平面,如下图:
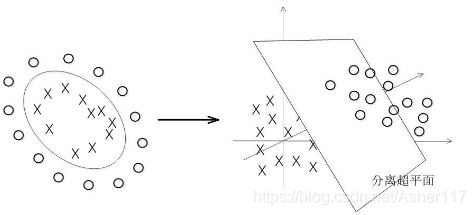 核函数相当于在原来的分类函数上套了一层函数:
核函数相当于在原来的分类函数上套了一层函数:
f ( x ) = w T x + b = ∑ i = 1 n α i y i < x i T , x > + b f(x)=w^Tx+b=\sum_{i=1}^n\alpha _iy_i<x_i^T,x>+b f(x)=wTx+b=∑i=1nαiyi<xiT,x>+b
在增加核函数 k k k之后, f ( x ) f(x) f(x)映射成为:
f ( x ) = w T x + b = ∑ i = 1 n α i y i < ϕ ( x i T ) , ϕ ( x ) > + b f(x)=w^Tx+b=\sum_{i=1}^n\alpha _iy_i<\phi (x_i^T),\phi (x)>+b f(x)=wTx+b=∑i=1nαiyi<ϕ(xiT),ϕ(x)>+b
其中 k < x i , x > = < ϕ ( x i ) , ϕ ( x ) > k<x_i,x>=<\phi (x_i),\phi (x)> k<xi,x>=<ϕ(xi),ϕ(x)>
3.2 核函数举例
核函数有很多种,常见的核函数见4.4小节。这里举例子展示一下多项式核函数,我们知道上面的提到的下图需要用圆来定义划分超平面,涉及到 x 1 , x 1 2 , x 2 , x 2 2 , x 1 x 2 x_1,x_1^2,x_2,x_2^2,x_1x_2 x1,x12,x2,x22,x1x2这样的五维空间来计算,如果直接定义五维空间也行,但是如果是3个变量将变成19维空间,后面呈指数爆炸型增长,因此不可取。
而核函数则可以在低维空间计算,然后将结果映射到高维空间,比如这里取下面多项式核函数:
( k < x 1 , x 2 > + 1 ) 2 (k<x_1,x_2>+1)^2 (k<x1,x2>+1)2,则只需要在二维空间中计算,然后结果同样是映射到了5维空间,大大的减少了计算量。

![]()
四、SVM公式推导用到的知识简介
4.1 凸集
SVM需要用到凸优化问题,在了解凸优化问题之前,需要先了解凸集和凸函数。
凸集的定义:凸集是一个点集,其中每两点之间的直线上的点都落在该点集中。
如下图所示,左边为凸集,而右边为非凸集。

4.2凸函数
凸函数的定义:一个定义在向量空间的凸子集C(区间)上的实值函数f,如果在其定义域C上的任意两点x,y以及 θ ∈ [ 0 , 1 ] \theta∈[0,1] θ∈[0,1]有:
f ( θ x + ( 1 − θ ) y ) < = θ f ( x ) + ( 1 − θ ) f ( y ) f(\theta x + (1-\theta)y)<=\theta f(x)+(1-\theta)f(y) f(θx+(1−θ)y)<=θf(x)+(1−θ)f(y)
 则该函数为凸函数!凸函数另一个判别方式是:如果一个凸函数是一个二阶可微函数,则它的二阶导数是非负的。
则该函数为凸函数!凸函数另一个判别方式是:如果一个凸函数是一个二阶可微函数,则它的二阶导数是非负的。
4.3 凸优化
凸优化定义:凸优化是指一种比较特殊的优化,是指求取最小值的目标函数为凸函数的一类优化问题。其中,目标函数为凸函数且定义域为凸集的优化问题称为无约束凸优化问题。而目标函数和不等式约束函数均为凸函数,等式约束函数为仿射函数,并且定义域为凸集的优化问题为约束优化问题。

4.4常用核函数
五、离群点处理
如下图,当存在离群点(outlier)的时候,有时候会对结果产生很大的影响,因为超平面本身就是只有少数几个 support vector 组成的,如果这些 support vector 里又存在 outlier 的话,其影响就很大了。
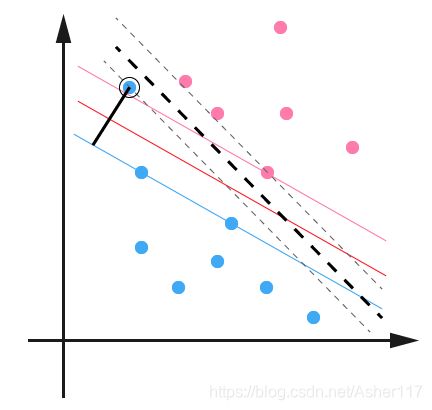

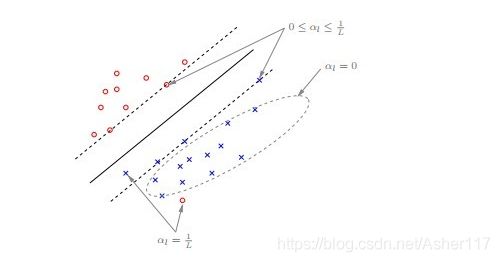
对于远离分类平面的点值为0;对于边缘上的点值在[0, 1/L]之间,其中,L为训练数据集个数,即数据集大小;对于outline数据和内部的数据值为1/L。
六、主要参数
实现SVM现在都有比较好用的包,可以直接调用,但是有几个主要的参数需要知道。
6.1 参数C
参数C表示的是惩罚系数,即上面说到的对误差(离群点)的宽容度,C越高,说明越不能容忍出现误差,容易过拟合,C越小,容易欠拟合,C过大或过小,泛化能力变差。
6.2 参数kernel
参数kernel为核函数,默认为rbf(高斯核函数),其他值还有linear、poly、sigmoid、precomputed等。
6.3 参数gamma
参数gamma是‘rbf’,‘poly’ 和‘sigmoid’核函数参数。隐含地决定了数据映射到新的特征空间后的分布,gamma越大,支持向量越少,gamma值越小,支持向量越多。支持向量的个数影响训练与预测的速度。默认为 1 / n f e a t u r e s 1/n_{features} 1/nfeatures。
参考文献:
李航 《统计学习方法》
https://blog.csdn.net/Asher117/article/details/94733777
https://blog.csdn.net/v_july_v/article/details/7624837
https://www.zhihu.com/question/20466147
https://blog.csdn.net/feilong_csdn/article/details/62427148
https://blog.csdn.net/batuwuhanpei/article/details/52354822
https://zhidao.baidu.com/question/311993614.html
https://www.cnblogs.com/en-heng/p/5965438.html







