学习笔记：Caffe上LeNet模型理解

学习笔记：Caffe上LeNet模型理解

Caffe中用的模型结构是著名的手写体识别模型LeNet-5（http://yann.lecun.com/exdb/lenet/a35.html）。当年美国大多数银行就是用它来识别支票上面的手写数字的。能够达到这种商用的地步，它的准确性可想而知，唯一的区别是把其中的sigmoid激活函数换成了ReLU。

为什么换成ReLU，上一篇blog中找到了一些相关讨论，可以参考。

CNN的发展，关键就在于，通过卷积（convolution http://deeplearning.stanford.edu/wiki/index.php/Feature_extraction_using_convolution）和降采样（pooling http://deeplearning.stanford.edu/wiki/index.php/Pooling ）能够成功的减少需要训练的参数值，回头去看SparseAutoEncoder 更会有明显的感觉。

具体需要训练多少个参数，http://blog.csdn.net/zouxy09/article/details/8781543 有做一个对应的推算，可以参考。

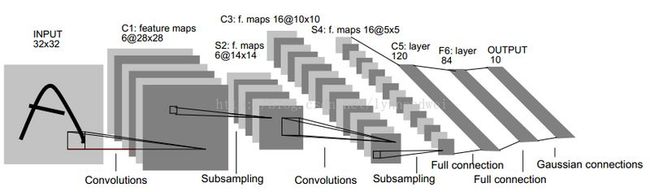
这是一个原始的LeNet模型图

 

在Caffe中，这个结构进行了一些修改。结构定义在$caffe-master/examples/mnist/lenet_train_test.prototxt中。

需要对google protobuf有一定了解并且看过Caffe中protobuf的定义，其定义在$caffe-master/src/caffe/proto/caffe.proto。
protobuf是google公司的一个开源项目，主要功能是把某种数据结构的信息以某种格式保存及传递，类似微软的XML，但是效率较高。目前提供C++、java和python的API。
protobuf简介：http://blog.163.com/jiang_tao_2010/blog/static/12112689020114305013458/
使用实例       ：http://www.ibm.com/developerworks/cn/linux/l-cn-gpb/

 

Blob

Blob是用以存储数据的4维数组，例如

对于数据：Number*Channel*Height*Width

对于卷积权重：Output*Input*Height*Width

对于卷积偏置：Output*1*1*1

 

 

 

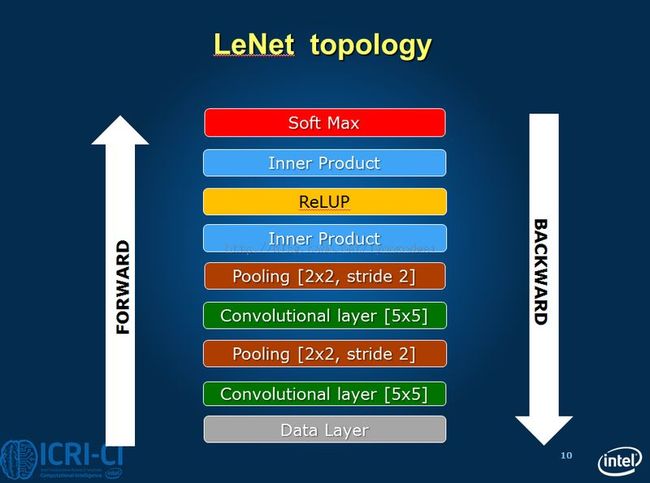
整个结构中包含两个convolution layer、两个pooling layer和两个fully connected layer。

每个层有多个Feature Map，每个Feature Map通过一种卷积滤波器提取输入的一种特征，然后每个Feature Map有多个神经元。

首先是数据层，测试数据100张为一批（batch_size），后面括号内是数据总大小。如100*28*28= 78400

 Top shape: 100 1 28 28 (78400)  

 Top shape: 100 1 1 1 (100)  

conv1(即产生图上 C1数据）层是一个卷积层，由20个特征图Feature Map构成。卷积核的大小是5*5。 通过卷积之后，数据变成（28-5+1）*（28-5+1），20个特征

 

我们是可以随机的初始化权重和偏差，使用xavier算法根据输入和输出的神经元数目来决定初始化的范围。

Top shape: 100 20 24 24 (1152000) 

pool1（即产生S2数据）是一个降采样层，有20个12*12的特征图。降采样的核是2*2的，所以数据变成12*12.

Top shape: 100 20 12 12 (288000)

conv2（即产生C3数据）是卷积层，核还是5*5，数据变成（12-5+1）*（12-5+1）。 50个特征

Top shape: 100 50 8 8 (320000)  

pool2（即产生S3数据）是降采样层，降采样核为2*2，则数据变成4*4

 Top shape: 100 50 4 4 (80000)  

 

ip1 是全连接层（产生C5的数据）。某个程度上可以认为是卷积层。输出为500. 原始模型中，从5*5的数据通过5*5的卷积得到1*1的数据。 现在的模型数据为4*4，得到的数据也是1*1，构成了数据中的全连接。

Top shape: 100 500 1 1 (50000)  

通过RELU 计算

Top shape: 100 500 1 1 (50000)  

 

ip2是第二个全连接层，输出为10，直接输出结果，数据的分类判断在这一层中完成。

 

I0303 18:26:32.104604 27313 net.cpp:96] Setting up ip2
I0303 18:26:32.104676 27313 net.cpp:103] Top shape: 100 10 1 1 (1000)
I0303 18:26:32.104691 27313 net.cpp:67] Creating Layer ip2_ip2_0_split
I0303 18:26:32.104701 27313 net.cpp:394] ip2_ip2_0_split <- ip2
I0303 18:26:32.104710 27313 net.cpp:356] ip2_ip2_0_split -> ip2_ip2_0_split_0
I0303 18:26:32.104722 27313 net.cpp:356] ip2_ip2_0_split -> ip2_ip2_0_split_1
I0303 18:26:32.104733 27313 net.cpp:96] Setting up ip2_ip2_0_split
I0303 18:26:32.104743 27313 net.cpp:103] Top shape: 100 10 1 1 (1000)

 Top shape: 100 10 1 1 (1000)  

数据变化对比如图

 

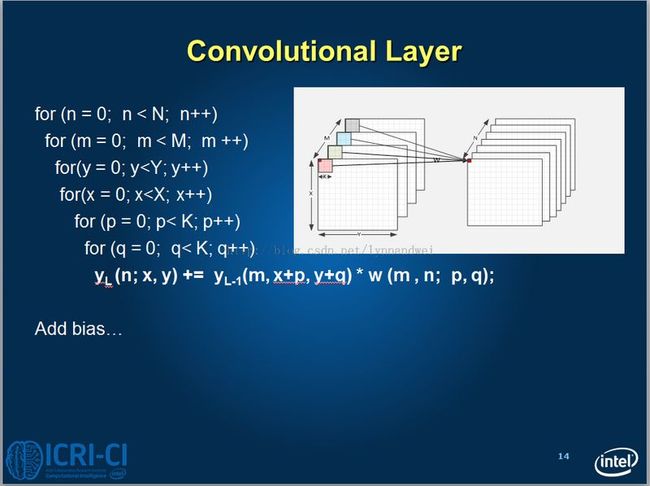
此外，从pool1到conv2， 整个过程应该是怎样的，也可以用图来表示，其中m=20, n = 50 x=y=12, k=5

 

ip1 虽然这一层有其他的数据操作，但是最终可以用如下的公式来进行计算。所以它也是全连接层

 

 

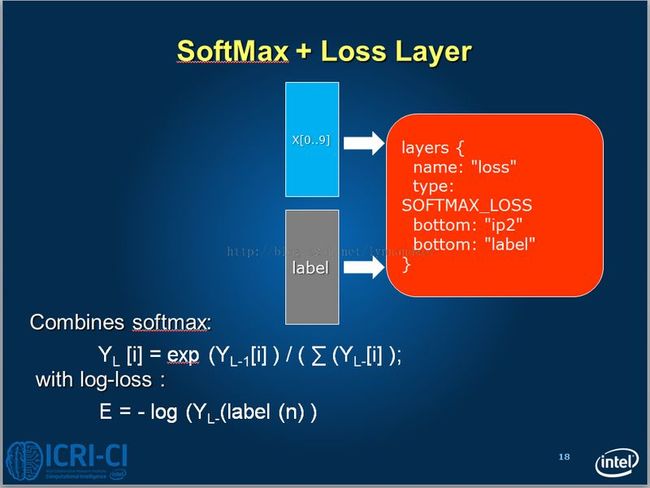
loss的公式

 

 

整个网络的反向求导具体如下：

资料可参照 http://blog.csdn.net/zouxy09/article/details/9993371  http://www.cnblogs.com/tornadomeet/p/3468450.html

 

I0303 18:26:32.104909 27313 net.cpp:170] loss needs backward computation.
I0303 18:26:32.104918 27313 net.cpp:172] accuracy does not need backward computation.
I0303 18:26:32.104925 27313 net.cpp:170] ip2_ip2_0_split needs backward computation.
I0303 18:26:32.104933 27313 net.cpp:170] ip2 needs backward computation.
I0303 18:26:32.104941 27313 net.cpp:170] relu1 needs backward computation.
I0303 18:26:32.104948 27313 net.cpp:170] ip1 needs backward computation.
I0303 18:26:32.104956 27313 net.cpp:170] pool2 needs backward computation.
I0303 18:26:32.104964 27313 net.cpp:170] conv2 needs backward computation.
I0303 18:26:32.104975 27313 net.cpp:170] pool1 needs backward computation.
I0303 18:26:32.104984 27313 net.cpp:170] conv1 needs backward computation.

 

 

 

参考文献

机器学习(Machine Learning)&深度学习(Deep Learning)资料  http://blog.csdn.net/zhoubl668/article/details/42921187

http://ml.memect.com/article/machine-learning-guide.html

http://www.cnblogs.com/tornadomeet/p/3468450.html

http://www.360doc.com/content/13/0729/19/13256259_303401668.shtml 
http://blog.sciencenet.cn/blog-1583812-843207.html
http://blog.csdn.net/qiaofangjie/article/details/16826849

http://blog.csdn.net/zouxy09/article/details/9993371

http://www.cnblogs.com/tornadomeet/archive/2013/05/05/3061457.html

http://blog.csdn.net/kkk584520/article/details/41694301

http://blog.csdn.net/ycheng_sjtu/article/details/39693655