腾讯面试题:50个阶梯,你一次可以上一阶或两阶,走上去,共有多少种走法【原】
本文转自:http://www.cnblogs.com/flowerszhong/archive/2011/09/14/2176374.html
有个同学去了腾讯,他说面试时有这么一道思维题:50个阶梯,你一次可以上一阶或两阶,走上去,共有多少种走法?
我的思路:
我的思维比较直线简单:
1,求出走上次可能有的方式,这里的方式是指:共走多少个1步,多少个2步。比如说,你走了2个1步,其余走2步,要走24个2步,用对象存起来就是:{one:2,two:24}
2,每个方式的走法是可以通过排列组合公式算出来的。如下是排列组合公式:
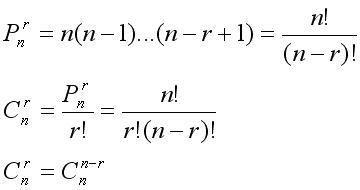
3,用到的公式是c(n,r)=n!/r!(n-r)!;这个比较好实现,无非就是阶乘除阶乘。
代码如下:
var waysArr = []; // 上台阶方式的,每一种方式为一个对象字面量,如[{one:2,two:24},{one:4,two:23}]
var counts = []; // 存每种方式排列组合数
// 生成waysArr
for ( var i = 25 ; i >= 0 ; i -- ) {
var x = 50 - 2 * i;
waysArr.push({ one: x, two: i });
}
// 阶乘
function factorial(num) {
if (num <= 1 ) {
return 1 ;
}
else {
return num * arguments.callee(num - 1 );
}
}
// 每种方式的排列数
// 参数是走1步的次数,走2步的次数
function thisWayTimes(one, two) {
// 排列组合公式: n!/r!(n-r)!
// 穷举--求得被除数
var ExhaustiveTimes = factorial(one + two);
// 重复的次数---求得除数
var repeatedTimes = factorial(one) * factorial(two);
// 算出次数---相除
var thisWayTime = ExhaustiveTimes / repeatedTimes;
// 存进数组
counts.push(thisWayTime);
}
// 计算每种方式的,除去全1全2,存入数组
for ( var j = 0 , waysLen = waysArr.length; j < waysLen; j ++ ) {
if (waysArr[j].one != 0 && waysArr[j].one != 50 ) {
thisWayTimes(waysArr[j].one, waysArr[j].two);
}
}
// 求和函数
function arrayNumSum(len) {
if (len <= 0 ) {
return 0 ;
} else {
return counts[len] + arguments.callee(len - 1 );
}
}
// 求和,包括全1全2
countsSum = arrayNumSum(counts.length - 1 ) + 2 ; // 计算出来共是20,365,010,749次
alert(countsSum);
})();
后来正解出来,我的答案是不对,又不全错,因为排列组合公式做了除法运算,js算出来的结果不精确。
(这就是没有找到真正数学规律的方案,费力不讨好)
peter.liu的思路:
代码如下:
function steps(n){
if (n === 1 )
return [ ' O ' , ' T1 ' ]; // 第一步两种可能
lastSteps = steps(n - 1 );
var currentSteps = [];
for ( var i = 0 ; i < lastSteps.length; i ++ ){
var lastStep = lastSteps[i];
if (lastStep === ' O ' || lastStep === ' T2 ' )
currentSteps.push( ' O ' , ' T1 ' );
else if (lastStep === ' T1 ' )
currentSteps.push( ' T2 ' );
}
return currentSteps;
}
var result = steps( 20 );
result = result.filter( function (item, index){ return item !== ' T1 ' }); // 最后一步不能是'T1', 过滤掉
console.log(result.length);
})();
(这种思路很好,很巧妙,可惜就是运算量太大)
费波拉希数列:
peter的方法虽然不能求得50层的次数,但是可以求得前30多层。依次如下:
一共1个台阶的话有1种走法.
一共2个台阶的话有2种走法.
一共3个台阶的话有3种走法.
一共4个台阶的话有5种走法.
一共5个台阶的话有8种走法.
一共6个台阶的话有13种走法.
一共7个台阶的话有21种走法.
一共8个台阶的话有34种走法.
一共9个台阶的话有55种走法.
一共10个台阶的话有89种走法.
一共11个台阶的话有144种走法.
一共12个台阶的话有233种走法.
一共13个台阶的话有377种走法.
一共14个台阶的话有610种走法.
一共15个台阶的话有987种走法.
一共16个台阶的话有1597种走法.
一共17个台阶的话有2584种走法.
一共18个台阶的话有4181种走法.
一共19个台阶的话有6765种走法.
一共20个台阶的话有10946种走法.
一共21个台阶的话有17711种走法.
一共22个台阶的话有28657种走法.
一共23个台阶的话有46368种走法.
一共24个台阶的话有75025种走法.
一共25个台阶的话有121393种走法.
一共26个台阶的话有196418种走法.
一共27个台阶的话有317811种走法.
一共28个台阶的话有514229种走法.
一共29个台阶的话有832040种走法.
一共30个台阶的话有1346269种走法.
一共31个台阶的话有2178309种走法.
一共32个台阶的话有3524578种走法.
一共33个台阶的话有5702887种走法.
一共34个台阶的话有9227465种走法.
一共35个台阶的话有14930352种走法.
这不正是个费波拉希数列!!!!
知道这个数学规律就好办了。代码如下:
function fib(n) {
return function (n, a, b) {
return n > 0 ? arguments.callee(n - 1 , b, a + b) : a;
} (n, 0 , 1 );
}
fib( 0 ); // 0
fib( 1 ); // 1
fib( 2 ); // 1
fib( 3 ); // 2
fib( 4 ); // 3
// ......
fib( 50 ); // 12586269025
fib( 51 ); // 20365011074,这里是上到第50个阶梯