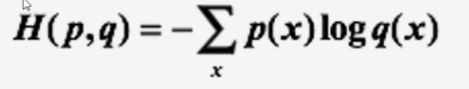TensorFlow应用示例（线性+非线性）

一、实现线性回归

版本：TensorFlow1.0

需求：假设有100个点，点的分布满足y=1.5*x+2.3，实现该模型。

步骤分析：

1.准备数据集：满足y=1.5x+2.3的100个样本

2.建立线性模型：

•  随机初始化w和b
• y=w·x+b，目标：求出权重w和偏置b
• 确定损失函数（预测值与真实值之间的误差）--均差误差
• 梯度下降优化损失：需要指定学习率（超参数）

3.实现

import tensorflow as tf

"""
实现线性回归
y=1.5x+2.3
"""

#1）准备数据集
with tf.variable_scope("set_data"):
    #生成100个数x，平均=2，标准差=2
    x_true = tf.random_normal(shape=(100,1),mean=2,stddev=2)
    #生成y值
    y_true = tf.matmul(x_true,[[1.5]])+2.3
#2）建立线性模型
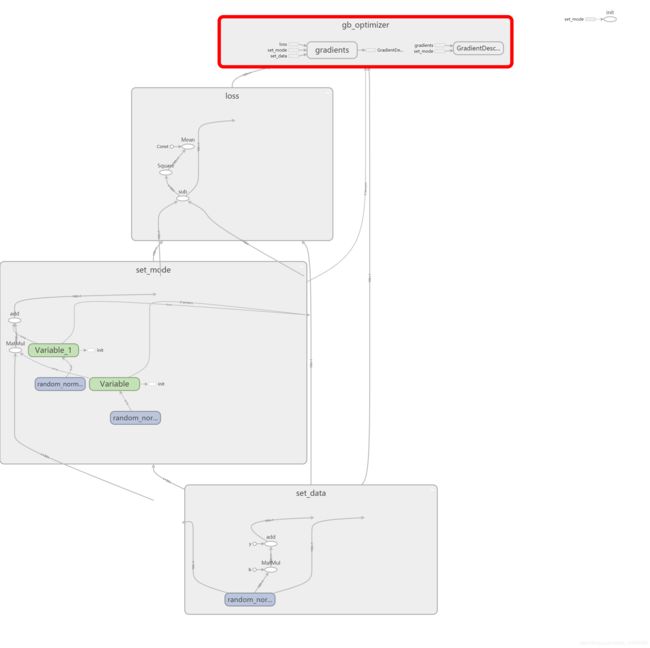
with tf.variable_scope("set_mode"):
# y=W·x+b ，目标：求出权重W和偏置b
#随机初始化w1和b1
#不想训练的属性：trainable=True
    wieights = tf.Variable(initial_value=tf.random_normal(shape=(1,1)))
    bias = tf.Variable(initial_value=tf.random_normal(shape=(1,1)))
    y_predict = tf.matmul(x_true,wieights)+bias
#3)确定损失函数--均方误差
with tf.variable_scope("loss"):
    error = tf.reduce_mean(tf.square(y_predict-y_true))
#4）梯度下降优化损失
with tf.variable_scope("gb_optimizer"):
# w = w-学习率*（方向）
# b = b-学习率*（方向）
    optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(error)

#初始化变量
init = tf.global_variables_initializer()
#开启会话
with tf.Session() as sess:
    tf.summary.FileWriter("./tensorboard/",graph=sess.graph)
    sess.run(init)
    print("随机初始化权重：%f,偏置：%f" %(wieights.eval(),bias.eval()))
    # 训练模型
    for i in range(1000):
        sess.run(optimizer)
        if(i%10==0):
            print("第%d步的误差为:%f,，权重为:%f，偏置为:%f" %(i,error.eval(),wieights.eval(),bias.eval()))

4.运行结果：

随机初始化权重：1.783771,偏置：-1.073572
第0步的误差为:6.481601,，权重为:1.882007，偏置为:-1.017843
第10步的误差为:4.744476,，权重为:2.206448，偏置为:-0.634838
第20步的误差为:3.435728,，权重为:2.169200，偏置为:-0.357392
第30步的误差为:3.782405,，权重为:2.171374，偏置为:-0.134230
第40步的误差为:2.643008,，权重为:2.078105，偏置为:0.066570
第50步的误差为:2.239186,，权重为:2.020358，偏置为:0.272639
第60步的误差为:1.671945,，权重为:1.967707，偏置为:0.455575
第70步的误差为:1.273096,，权重为:1.962153，偏置为:0.634436
第80步的误差为:0.905109,，权重为:1.909945，偏置为:0.780773
第90步的误差为:0.803095,，权重为:1.869004，偏置为:0.906332
第100步的误差为:0.889608,，权重为:1.841831，偏置为:1.030817
第110步的误差为:0.631504,，权重为:1.797644，偏置为:1.147289
第120步的误差为:0.444711,，权重为:1.772158，偏置为:1.255469
第130步的误差为:0.517370,，权重为:1.757893，偏置为:1.349874
第140步的误差为:0.323332,，权重为:1.735925，偏置为:1.433802
第150步的误差为:0.274140,，权重为:1.709675，偏置为:1.507691
第160步的误差为:0.279660,，权重为:1.691628，偏置为:1.581163
第170步的误差为:0.247056,，权重为:1.672582，偏置为:1.644922
第180步的误差为:0.219824,，权重为:1.660950，偏置为:1.704900
第190步的误差为:0.125070,，权重为:1.642655，偏置为:1.755131
第200步的误差为:0.120266,，权重为:1.627645，偏置为:1.807713
第210步的误差为:0.094889,，权重为:1.616603，偏置为:1.852330
第220步的误差为:0.081407,，权重为:1.609755，偏置为:1.892995
第230步的误差为:0.076439,，权重为:1.598043，偏置为:1.927986
第240步的误差为:0.054179,，权重为:1.589612，偏置为:1.961250
第250步的误差为:0.035392,，权重为:1.583712，偏置为:1.991163
第260步的误差为:0.044145,，权重为:1.575317，偏置为:2.019429
第270步的误差为:0.032002,，权重为:1.570472，偏置为:2.044106
第280步的误差为:0.027537,，权重为:1.560451，偏置为:2.068831
第290步的误差为:0.024574,，权重为:1.556200，偏置为:2.090067
第300步的误差为:0.014941,，权重为:1.552455，偏置为:2.108541
第310步的误差为:0.010752,，权重为:1.547268，偏置为:2.125536
第320步的误差为:0.011338,，权重为:1.543422，偏置为:2.141800
第330步的误差为:0.009505,，权重为:1.537688，偏置为:2.155502
第340步的误差为:0.008204,，权重为:1.533388，偏置为:2.168386
第350步的误差为:0.007419,，权重为:1.531933，偏置为:2.180761
第360步的误差为:0.006773,，权重为:1.529602，偏置为:2.190964
第370步的误差为:0.004246,，权重为:1.525752，偏置为:2.200973
第380步的误差为:0.003970,，权重为:1.523309，偏置为:2.209746
第390步的误差为:0.002699,，权重为:1.521409，偏置为:2.218345
第400步的误差为:0.002898,，权重为:1.519485，偏置为:2.226065
第410步的误差为:0.002250,，权重为:1.517278，偏置为:2.232943
第420步的误差为:0.001853,，权重为:1.515805，偏置为:2.238975
第430步的误差为:0.001705,，权重为:1.514264，偏置为:2.244419
第440步的误差为:0.001188,，权重为:1.513913，偏置为:2.249554
第450步的误差为:0.000912,，权重为:1.512291，偏置为:2.253895
第460步的误差为:0.001034,，权重为:1.510908，偏置为:2.258123
第470步的误差为:0.000840,，权重为:1.510466，偏置为:2.261988
第480步的误差为:0.000525,，权重为:1.509404，偏置为:2.265493
第490步的误差为:0.000625,，权重为:1.508530，偏置为:2.268559
第500步的误差为:0.000362,，权重为:1.507587，偏置为:2.271465
第510步的误差为:0.000333,，权重为:1.506834，偏置为:2.274108
第520步的误差为:0.000255,，权重为:1.506202，偏置为:2.276434
第530步的误差为:0.000226,，权重为:1.505686，偏置为:2.278610
第540步的误差为:0.000195,，权重为:1.505098，偏置为:2.280498
第550步的误差为:0.000153,，权重为:1.504679，偏置为:2.282368
第560步的误差为:0.000142,，权重为:1.504213，偏置为:2.283978
第570步的误差为:0.000108,，权重为:1.503928，偏置为:2.285373
第580步的误差为:0.000092,，权重为:1.503583，偏置为:2.286684
第590步的误差为:0.000072,，权重为:1.503191，偏置为:2.287752
第600步的误差为:0.000058,，权重为:1.502892，偏置为:2.288891
第610步的误差为:0.000048,，权重为:1.502692，偏置为:2.289927
第620步的误差为:0.000043,，权重为:1.502469，偏置为:2.290845
第630步的误差为:0.000031,，权重为:1.502158，偏置为:2.291655
第640步的误差为:0.000036,，权重为:1.502025，偏置为:2.292397
第650步的误差为:0.000019,，权重为:1.501808，偏置为:2.293069
第660步的误差为:0.000027,，权重为:1.501634，偏置为:2.293711
第670步的误差为:0.000019,，权重为:1.501564，偏置为:2.294302
第680步的误差为:0.000015,，权重为:1.501405，偏置为:2.294799
第690步的误差为:0.000012,，权重为:1.501261，偏置为:2.295244
第700步的误差为:0.000008,，权重为:1.501173，偏置为:2.295678
第710步的误差为:0.000008,，权重为:1.501043，偏置为:2.296060
第720步的误差为:0.000009,，权重为:1.500945，偏置为:2.296410
第730步的误差为:0.000004,，权重为:1.500905，偏置为:2.296731
第740步的误差为:0.000004,，权重为:1.500779，偏置为:2.297013
第750步的误差为:0.000004,，权重为:1.500714，偏置为:2.297271
第760步的误差为:0.000003,，权重为:1.500659，偏置为:2.297510
第770步的误差为:0.000002,，权重为:1.500621，偏置为:2.297744
第780步的误差为:0.000002,，权重为:1.500545，偏置为:2.297942
第790步的误差为:0.000001,，权重为:1.500474，偏置为:2.298135
第800步的误差为:0.000001,，权重为:1.500452，偏置为:2.298300
第810步的误差为:0.000001,，权重为:1.500413，偏置为:2.298448
第820步的误差为:0.000001,，权重为:1.500375，偏置为:2.298599
第830步的误差为:0.000001,，权重为:1.500338，偏置为:2.298721
第840步的误差为:0.000001,，权重为:1.500311，偏置为:2.298838
第850步的误差为:0.000001,，权重为:1.500281，偏置为:2.298942
第860步的误差为:0.000000,，权重为:1.500243，偏置为:2.299042
第870步的误差为:0.000000,，权重为:1.500217，偏置为:2.299135
第880步的误差为:0.000000,，权重为:1.500210，偏置为:2.299216
第890步的误差为:0.000000,，权重为:1.500198，偏置为:2.299287
第900步的误差为:0.000000,，权重为:1.500167，偏置为:2.299349
第910步的误差为:0.000000,，权重为:1.500161，偏置为:2.299404
第920步的误差为:0.000000,，权重为:1.500143，偏置为:2.299459
第930步的误差为:0.000000,，权重为:1.500129，偏置为:2.299509
第940步的误差为:0.000000,，权重为:1.500116，偏置为:2.299551
第950步的误差为:0.000000,，权重为:1.500109，偏置为:2.299591
第960步的误差为:0.000000,，权重为:1.500100，偏置为:2.299628
第970步的误差为:0.000000,，权重为:1.500087，偏置为:2.299662
第980步的误差为:0.000000,，权重为:1.500085，偏置为:2.299692
第990步的误差为:0.000000,，权重为:1.500074，偏置为:2.299718

5.通过tensorboard查看模型建立过程：

6.模型的保存与加载：

tf.train.Saver(var_list=None,max_to_keep=5)

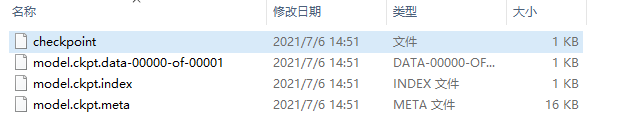
• 保存和加载模型（保存文件格式：checkpoint文件）
• var_list：指定要保存和还原的变量，它可以作为一个dict或一个列表传递
• max_to_keep：指示要保留的最近检查点文件的最大数量。创建新文件时，会删除较旧的文件。如果无或0，则保留所有检查点文件，默认为5（即保留最新的5个检查点文件）

#模型文件
saver = tf.train.Saver()
with tf.Session() as sess:
     if(error.eval()<0.000001):
            saver.save(sess,"./ckpt/model.ckpt")
    

保存的模型文件：

此时，如果我们想在已经训练好的基础上继续进行训练，可以加载已有的模型：

saver = tf.train.Saver()
saver.restore(sess,'/ckpt/model.ckpt')

#或者：
#如果判断模型是否存在，直接指定目录
checkpoint = tf.train.latest_checkpoint("./ckpt/")
saver.restore(sess,checkpoint)

二、实现非线性回归

实现思路：

1. 数据集加载、预处理
2. 特征工程
3. 模型搭建、训练、测试、优化（结果可视化）
4. 模型保存
5. 模型预测

import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt


#加载csv数据
data = pd.read_csv('./data/train.csv')
#显示数据
data.head()
#画图
plt.scatter(data.week_1,data.outputType)
#取列数据 左闭右开
data_train = data.iloc[:,2:6]
#统计结果分布
target_train.value_counts()

#构建模型
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(11,activation=tf.nn.relu,use_bias=True,input_shape=(4,)))
model.add(tf.keras.layers.Dense(11,activation=tf.nn.relu,use_bias=True))
model.add(tf.keras.layers.Dense(11,activation=tf.nn.relu,use_bias=True))
model.add(tf.keras.layers.Dense(1,activation=tf.nn.sigmoid,use_bias=True))
model.summary()
#设置网络参数
model.compile(
    optimizer=tf.keras.optimizers.Adam(learning_rate=0.01), #使用Adam优化器，学习率为0.1
    loss=tf.keras.losses.binary_crossentropy, #使用交叉熵处理sigm概率问题
   # loss=tf.keras.losses.sparse_categorical_crossentropy, #categorical_crossentropy[one-hot编码]和sparse_categorical_crossentropy[数字编码]处理softmax多分类
    metrics=['acc'] #标注网络评价指标
   # metrics=['sparse_categorical_accuracy']
)
#进行学习
history = model.fit(
    data_train,
    target_train,
    epochs = 500, #迭代次数epochs为500
    validation_data = (data.iloc[70:170,2:6],data.iloc[70:170,-1])
)
#进行预测
model.predict(test_data)
#对网络打分
model.evaluate(test_data,test_target)

---

交叉熵损失函数：

交叉熵实际输出（概率）与 期望输出（概率）的距离，也就是交叉熵的值越小，两个概率分布就越接近，假设概率分布  为p为期望输出，概率分布q为数据输出，H（p,q）为交叉熵，则：假设概率分布p为期望输出，概率分布q为实际输出，H（p,q）为交叉熵，则：

 

 

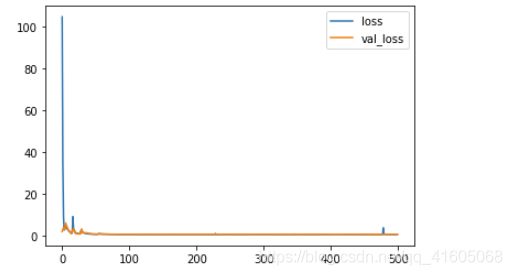
对网络性能分析：

#获取捕捉到的值
history.history.keys()
#查看损失对比
plt.plot(history.epoch,history.history.get('loss'),label='loss')
plt.plot(history.epoch,history.history.get('val_loss'),label='val_loss')
plt.legend()

 三、Subclassing model 模型子类化（常用）

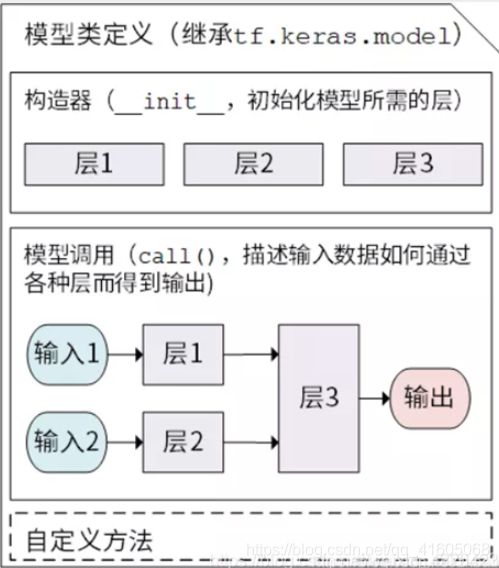
上述一、二中的模型定义显得有些流水账，如何使用面向对象的思想来定义模型呢？也就是模型子类化。

TensorFlow 2.0通过Keras Subclassing API支持这种开箱即用的方式。在keras中Model类做为基本的类，可以在些基础上，进行会任意个人设置，带来很强的自由。但同时带来的不足就是没用序列和函数定义模型使用起来简单。

实现：

import tensorflow as tf
import pandas as pd
import numpy as np


class MyModel(tf.keras.Model):
    def __init__(self):
        super(MyModel,self).__init__(name="my_model")
        self.dense1  = tf.keras.layers.Dense(11,activation=tf.nn.relu,use_bias=True)
        self.dense2  = tf.keras.layers.Dense(11,activation=tf.nn.relu,use_bias=True)
        self.dense3 = tf.keras.layers.Dense(1,activation=tf.nn.sigmoid,use_bias=True)
        
    def call(self,inputs):
        x = self.dense1(inputs)
        x = self.dense2(x)
        return self.dense3(x)



model = MyModel()

四、模型评估

机器学习的目标：泛化误差小

---

误差：学习器的预测输出和样本的真实标记输出之间的差异

训练误差：训练集上的误差

泛化误差：在新样本上的误差

过拟合：学习过度，在训练集上表现良好，在新样本上泛化误差很大

欠拟合：学习不足，没有学习到样本的通用特征