NSGA-II改进之非均匀变异
NSGA-II改进之非均匀变异
- 1-变异方式的选择
- 2-非均匀变异方式介绍
- 3-MATLAB代码实现
- 4-对比
-
- 4.1-ZDT函数比较
- 4.2-分析
- 5-总结
1-变异方式的选择
在进化算法中,多项式的变异方式,变异算子的作用与进化代数是没有关系的,所以当算法演化到一定代数的时候,算法会缺乏局部搜索能力。为了将变异算子的作用与代数关联起来,使得算法可以在前期变异的范围会较大,随着演化代数的增加,变异范围越来越小,增加算法的微调能力。Z.Michalewicz提出了非均匀变异。
2-非均匀变异方式介绍
设 x = ( x 1 , x 2 , . . . x n ) 为待变异个体,变异产生一个新基因 y ,首先随机生成一个整数 k ∈ [ 1 , n ] 然后对 x 的第 k 个基因 进行变异。 \begin{aligned} &设x=(x_1,x_2,...x_n)为待变异个体,变异产生一个新基因y,首先随机生成一个整数k\in[1,n]然后对x的 第k个基因\\&进行变异。 \end{aligned} \\ 设x=(x1,x2,...xn)为待变异个体,变异产生一个新基因y,首先随机生成一个整数k∈[1,n]然后对x的第k个基因进行变异。
y k = { x k + Δ ( t , u k − x k ) i f x ≤ 0.5 x k − Δ ( t , u k − x k ) e l s e y_k=\{ \begin{aligned} & x_k+\Delta(t,u_k-x_k)\quad if \quad x\leq 0.5 \\& x_k-\Delta(t,u_k-x_k)\quad else \end{aligned} \\ yk={xk+Δ(t,uk−xk)ifx≤0.5xk−Δ(t,uk−xk)else
则产生的新个体为 y = ( x 1 , x 2 , . . , x k , . . . , x n ) 。 其中随机数 r ∈ ( 0 , 1 ) , t 为当前进化代数,函数 Δ ( t , z ) 返回的是一个 [ 0 , z ] 的值,并且随 t 的增加 , 函数 Δ ( t , z ) 趋于 0 的概率增加。函数 Δ ( t , z ) 的特性使算法在前期具有较大的搜索范围,在后期可以进行小范围的调整。其中函数 Δ ( t , z ) 表示为: Δ ( t , z ) = z . ( 1 − r ( 1 − t / T ) b ) 上式中 r 是一个 0 到 1 的随机数, T 表示最大演化代数, b 是一个分均匀度的参数,一般取值为 2 到 5 。 \begin{aligned}& 则产生的新个体为y=(x_1,x_2,..,x_k,...,x_n)。 \\& 其中随机数r\in(0,1),t为当前进化代数,函数\Delta (t,z)返回的是一个[0,z]的值,并且随t的增加,函数\Delta (t,z)趋于0 \\& 的概率增加。函数 \Delta (t,z)的特性使算法在前期具有较大的搜索范围,在后期可以进行小范围的调整。其中函数\Delta (t,z)\\& 表示为: \end{aligned} \\ \Delta (t,z) = z.(1-r^(1-t/T)^b) \\ \begin{aligned}& 上式中r是一个0到1的随机数,T表示最大演化代数,b是一个分均匀度的参数,一般取值为2到5。 \quad \quad \quad \quad \quad \quad \quad \quad \end{aligned} 则产生的新个体为y=(x1,x2,..,xk,...,xn)。其中随机数r∈(0,1),t为当前进化代数,函数Δ(t,z)返回的是一个[0,z]的值,并且随t的增加,函数Δ(t,z)趋于0的概率增加。函数Δ(t,z)的特性使算法在前期具有较大的搜索范围,在后期可以进行小范围的调整。其中函数Δ(t,z)表示为:Δ(t,z)=z.(1−r(1−t/T)b)上式中r是一个0到1的随机数,T表示最大演化代数,b是一个分均匀度的参数,一般取值为2到5。
3-MATLAB代码实现
function child_pop = MyGA_mutate(parent_pop,dimension,bounds,t,T,x)
% t当前进进化次数,T最大迭代次数,x,问题编号
%GA算法
parent_pop = sortrows(parent_pop,[2+dimension+1,-(2+dimension+2)]);
parent_pop = parent_pop(:,1:dimension);
[popsize,~] = size(parent_pop);
%定义交叉变异的概率
mutation = 0.6;
%变异参数。b影响变异的范围。
b = 3;
child = [];
% 每个变异个体只做随机的单点变异
for i = 1:popsize
%判断个体是否进行遗传操作
m_r = rand(1);
if m_r < mutation
k = randperm(dimension,1); % 取一个整数,确定变异点
rk = rand(1);
child1 = parent_pop(i,:);
if rk >= 0.5 % 变异计算
z = bounds(k,2) - parent_pop(i,k);
xk = parent_pop(i,k) + z*(1-rand^((1-t/T)^b));
child1(1,k) = xk;
else
z = parent_pop(i,k) - bounds(k,1);
xk = parent_pop(i,k) - z*(1-rand^((1-t/T)^b));
child1(1,k) = xk;
end
child = [child;child1];
end
end
child_eva = calculation(child,x);
child_pop = [child,child_eva];
4-对比
只对比变异方式的不同,其余策略保持一致。
初始化:随机初始化
父代选择:锦标赛选择方式
交叉方式:多项式交叉
4.1-ZDT函数比较
| 非均匀变异 | 多项式变异 |
|---|---|
ZDT1 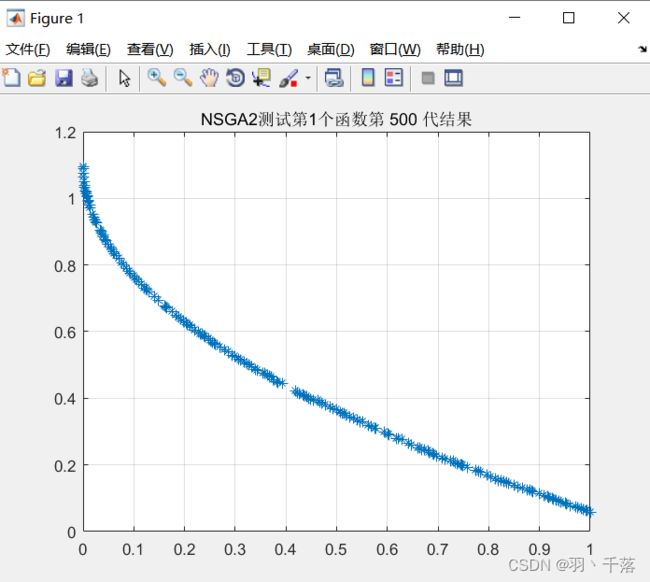 |
ZDT1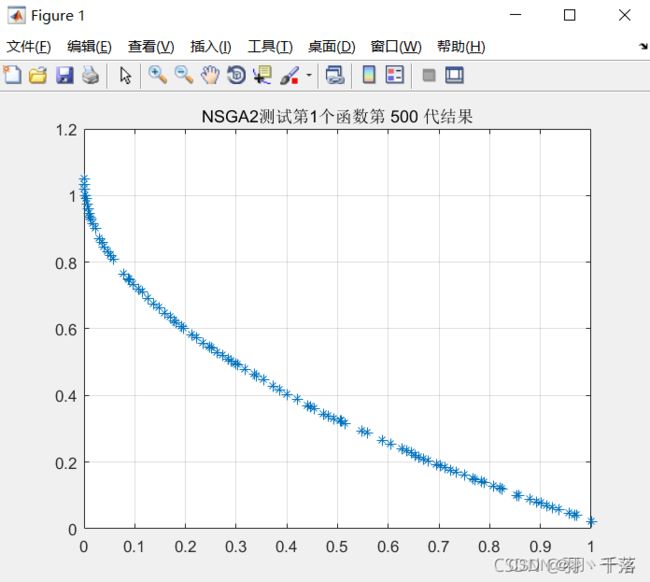 |
ZDT2 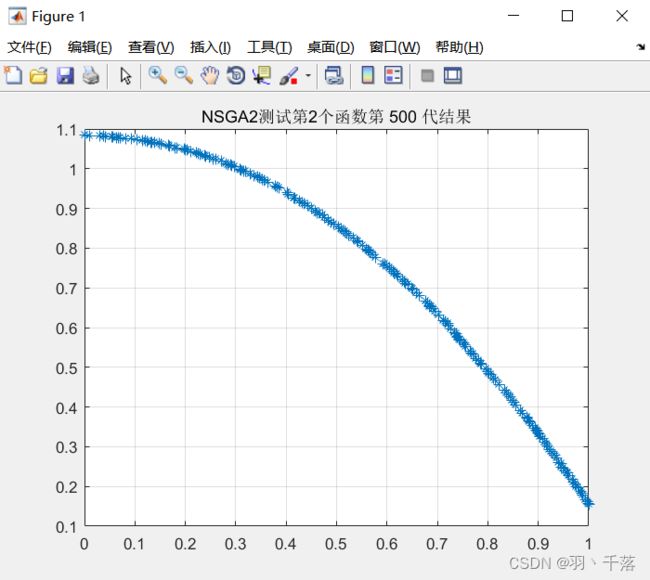 |
ZDT2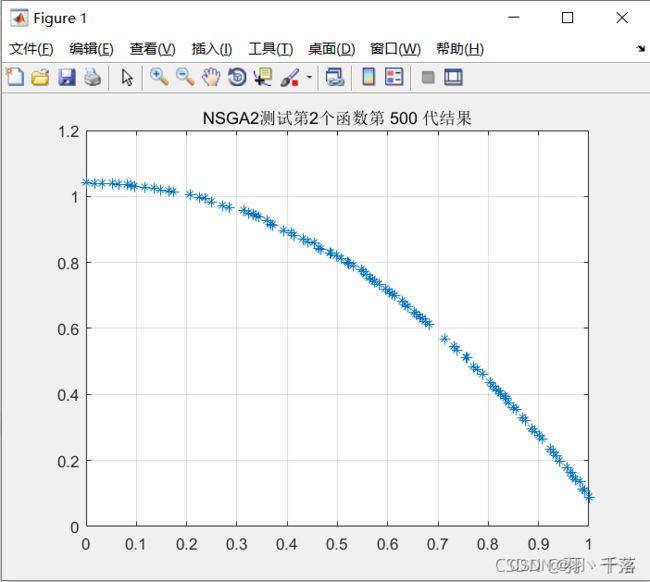 |
ZDT3 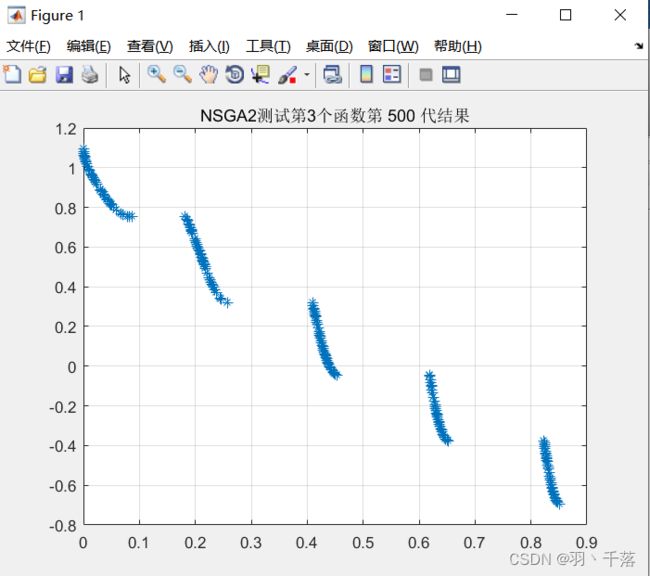 |
ZDT3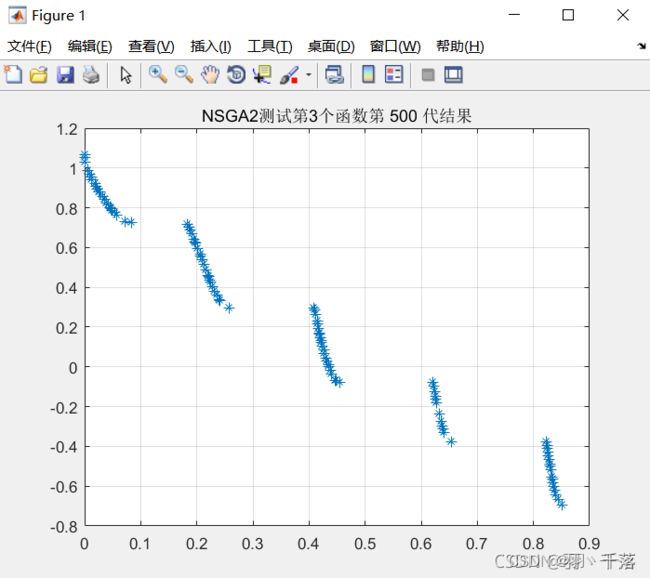 |
ZDT4 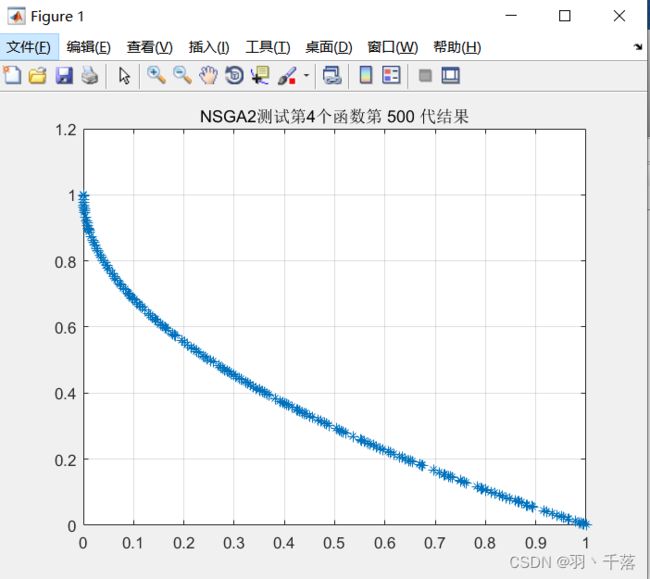 |
ZDT4 |
ZDT6  |
ZDT6 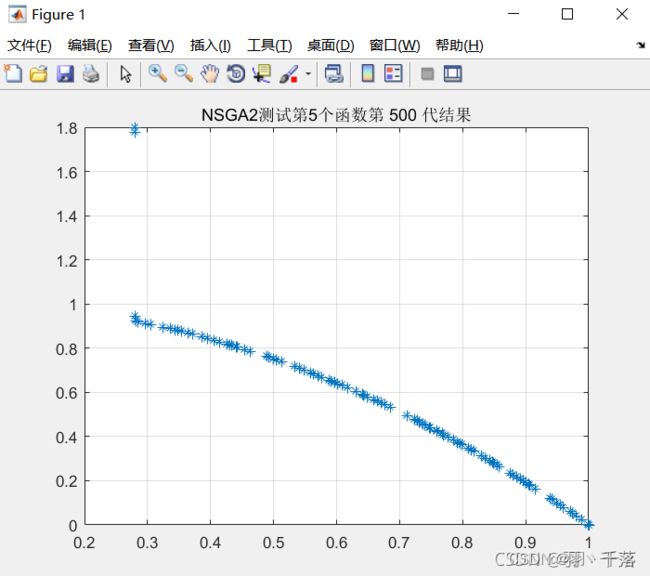 |
4.2-分析
从4.1的对比可以看出,采用非均匀变异和多项式变异的最大区别在ZDT4上,采用非均匀变异在ZDT4函数的求解中,是可以求得最佳前言的,而多项式变异在500代的时候依然差很远。而其他函数比较中,两者相差不远,甚至有些是多项式变异反而更优一点。
从非均匀变异的实现中,可以知道,越到后面,变异的范围就越小。所以最大迭代次数对变异有很大的影响,而多项式变异并不会受到这个方面的影响。
5-总结
算法步骤中实现策略的不同,效果也不同。一个策略的改变可能在某些方面上更优,但不一定在所有方面上都会更好。在针对不同问题的时候,对部分策略的改变也许就会得到更好的结果。
思考:
在【NSGA-II的算法介绍】中,多项式变异在处理超出边界的方案,是否合适呢?能否改为超出边界的时候,在范围空间中随机呢?这样做效果是否会更好呢?同样多项式交叉中的处理方式也是如此,改变之后的效果如何呢?多项式的交叉和变异也可以通过指数的变化控制变化范围,这个指数怎么取?是动态变化好还是固定好?