python与人工智能:神经网络和深度学习,卷积神经网络识别手写文字
深度学习是用于建立、模拟人脑进行分析学习的神经网络,并模仿人脑的机制来解释数据的一种机器学习 技术,卷积神经网络是其中最火热的技术。 如果要做事,想赶快入门,速度出活,请先死记住: 深度学习=多层的神经网络 ,如果要写论文,要作报告,要闲聊,请坚持一个原则:
深度学习绝不仅仅是多层的神经网络。
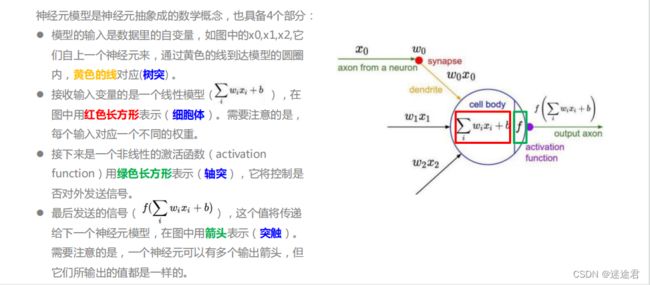
本质所谓神经网络问题的训练本质,就是已知 y1,y2....yn, 已知x1, x2....xm,求解每个连接的权值(w)和每个神经 元上的偏差值(b),使得最终偏差最小。训练对于以上求解w和b的值,一般都是通过 反向传播和梯度 下降 相结合来求解。就是一开始用随机数初始化我们每 个联结的权值,然后通过神经网络计算出来的y值跟真 实的y值做比对。如果这个值相差比较大,则修改当前 层的联结的权重。当发现这个值相差不大时,则修改更低一层的权重。这个步骤一直重复,逐步传递到第一层 的权值。
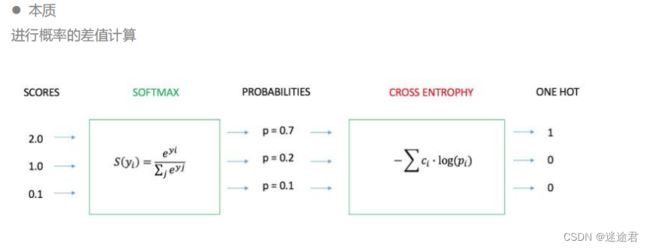
softmax在机器学习尤其是深度学习中,softmax是个非 常常用而且比较重要的函数,尤其在多分类的场 景中使用广泛。他把一些输入映射为0-1之间的 实数,并且归一化保证和为1,因此多分类的概 率之和也刚好为1。
损失函数(交叉熵)
下面我们用一个代码示例来演示神经网络模型:
神经网络模型创建步骤:
# 创建空白的神经网络
# 向空白神经网络中添加 一个层级,指定神经元的个数,输入、输出个数
# units: 该层输出数据的个数 input_dim:该层数据的输入个数,两个决定该层的神经元个数
# activation:该层神经元的激活函数
model1.add(Dense(units=1, input_dim=1, activation="relu"))
# 构造梯度下降的学习率(步长)的对象
adam = Adam(learning_rate=0.01)
# 设置步长和损失函数 "mse": 均方差
import numpy as np
import matplotlib.pyplot as plt
# 从keras框架中导入 神经网络的包
from keras import Sequential
# 从keras框架的 layers中导入层级包 Dense
from keras.layers import Dense
# 从 keras框架中导入 梯度下降的 学习率
from keras.optimizers import Adam
def load_data():
# 先假设 模型的 k=0.85 b=15
x = np.random.uniform(0, 85, (200, 1))
# 根据假模型,得到 y值
y = 0.9 * x + 15
# 将 x, 和 y在假模型直线附近进行正态分布
x = np.random.normal(x, 6)
y = np.random.normal(y, 6)
return x, y
def drawScatter(xx, yy):
plt.scatter(xx, yy, c='b')
plt.show()
def createModel():
# 创建空白的神经网络
model1 = Sequential()
# 向空白神经网络中添加 一个层级,指定神经元的个数,输入、输出个数
# units: 该层输出数据的个数 input_dim:该层数据的输入个数,两个决定该层的神经元个数
# activation:该层神经元的激活函数
model1.add(Dense(units=1, input_dim=1, activation="relu"))
# 构造梯度下降的学习率(步长)的对象
adam = Adam(learning_rate=0.01)
# 设置步长和损失函数 "mse": 均方差
model1.compile(adam, loss="mse")
return model1
def myfit_transform(model1, x_train, y_train):
plt.ion() # 开启绘图的交互模式,去除 show的影响
# 为了模型更优,因此训练多轮效果更好
for i in range(3000):
# 每训练一次,返回得到的模型的损失值
cost = model1.train_on_batch(x_train, y_train)
# 获取模型的权重值,应该是获取最后一层
w, b = model1.layers[-1].get_weights()
# 每个 100轮,打印模型的 k, b 值 和 模型的损失值
if i % 100 == 0:
print("轮次: {}: w: {}, b: {}, cost: {}".format(i, w, b, cost))
# 画出训练模型的回归线
xx = np.arange(0, 85, 0.1)
yy = w * xx + b
plt.cla() # 清除上一次的绘图数据
plt.xlim(0, 100) # 限制 图中 x坐标的范围
plt.ylim(0, 100) # 限制 图中 y坐标的范围
plt.scatter(x_train, y_train, color='b')
plt.scatter(xx, yy, c='r', s=3)
plt.pause(0.01) # 暂停,延时 10ms
plt.ioff() # 关闭绘图的交互模式
def model_evaluate(model1, xx, yy):
# 评估函数
cost = model1.evaluate(xx, yy)
print("cost: ", cost)
if __name__ == "__main__":
# 获得数据集
x, y = load_data()
# 搭建神经网络模型
model = createModel()
# 通过搭建的神经网络模型,进行训练学习,得到真正的 线性模型
myfit_transform(model, x, y)
# 模型评估
x_test = np.array([[40, ]])
y_test = 0.9*x_test+15
model_evaluate(model, x_test, y_test)
# 画出学习之后,模型的回归线
w, b = model.layers[-1].get_weights()
plt.plot(x_test, w * x_test + b, c="r")
# 通过训练模型进行预测
y_pre = model.predict(x_test)
print("预测:", y_pre)
print("真值:", 0.9 * x_test + 15)
# 画出真实点和预测点
plt.scatter(x_test, y_pre, c='y', marker="*")
plt.scatter(x_test, 0.9 * x_test + 15, c='g', marker='s')
drawScatter(x, y)
深度学习鸢尾花预测:
之前我们通过k近邻法来预测了鸢尾花的种类,但那是我们建立了一个假模型,现在我们利用神经网络模型来实现一下:
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from keras import Sequential
from keras.layers import Dense
from keras.optimizers import Adam
from keras.utils import to_categorical
def load_data():
data = load_iris()
return data.data, data.target
def createModel():
model1 = Sequential()
model1.add(Dense(input_dim=4, units=3, activation="softmax"))
adam = Adam(learning_rate=0.01)
model1.compile(optimizer=adam, loss="mse")
return model1
def model_fit(model1, xx, yy):
# 由于鸢尾花输出的结果有三种情况,三个类别出现的概率应该要一致
# 因此要对标签集的数据进行one-hot编码
yy = to_categorical(yy, num_classes=3)
# fit函数:进行模型训练
# batch_size:每轮训练的数据个数
# epochs: 训练的轮次 verbose:2表示最后一轮打印相关信息,1表示每一轮打印相关信息,0表示不打印
model1.fit(xx, yy, batch_size=100, epochs=2000, verbose=1)
print(yy)
def model_evaluate(model1, xx, yy):
yy = to_categorical(yy, num_classes=3)
cost = model1.evaluate(xx, yy)
print("cost: ", cost)
if __name__ == "__main__":
# 获得数据的训练集和标签集
x, y = load_data()
# 搭建神经网络模型
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.05)
model = createModel()
# 机器深度学习,得到真实模型
model_fit(model, x_train, y_train)
# 模型评估
model_evaluate(model, x_test, y_test)
# 预测,predict_classes多分类预测
pre = model.predict_classes(x_test)
print("预测:", pre)
print("真实: ", y_test)from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from keras import Sequential
from keras.layers import Dense
from keras.optimizers import Adam
from keras.utils import to_categorical
def load_data():
data = load_iris()
return data.data, data.target
def createModel():
model1 = Sequential()
model1.add(Dense(input_dim=4, units=3, activation="softmax"))
adam = Adam(learning_rate=0.01)
model1.compile(optimizer=adam, loss="mse")
return model1
def model_fit(model1, xx, yy):
# 由于鸢尾花输出的结果有三种情况,三个类别出现的概率应该要一致
# 因此要对标签集的数据进行one-hot编码
yy = to_categorical(yy, num_classes=3)
# fit函数:进行模型训练
# batch_size:每轮训练的数据个数
# epochs: 训练的轮次 verbose:2表示最后一轮打印相关信息,1表示每一轮打印相关信息,0表示不打印
model1.fit(xx, yy, batch_size=100, epochs=2000, verbose=1)
print(yy)
def model_evaluate(model1, xx, yy):
yy = to_categorical(yy, num_classes=3)
cost = model1.evaluate(xx, yy)
print("cost: ", cost)
if __name__ == "__main__":
# 获得数据的训练集和标签集
x, y = load_data()
# 搭建神经网络模型
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.05)
model = createModel()
# 机器深度学习,得到真实模型
model_fit(model, x_train, y_train)
# 模型评估
model_evaluate(model, x_test, y_test)
# 预测,predict_classes多分类预测
pre = model.predict_classes(x_test)
print("预测:", pre)
print("真实: ", y_test)卷积神经网络
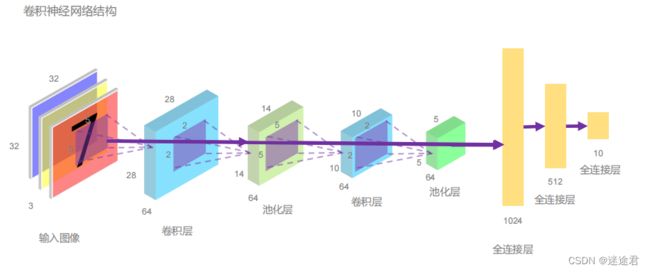
卷 积 神 经 网 络 ( Convolutional Neural Networks,CNN)是一类包含卷积计算且具有深度结构的前馈神经 网络 ( Feedforward Neural Networks ) 是 深 度 学 习(deep learning)的代表算法之一。卷积神经网络是一种多层神经网络,擅长处理图像处理、图像识别、语音识别等。 卷积网络本质上是一种输入到输出的映射,它能够 学习大量 的输入与输出之间的映射关系,而 不需要 任何输入和 输出之间的精确的数学表达式 ,只要用已知的模式对卷积网络加以训练,网络就具有输入输出对之间的映射能 力
卷积层
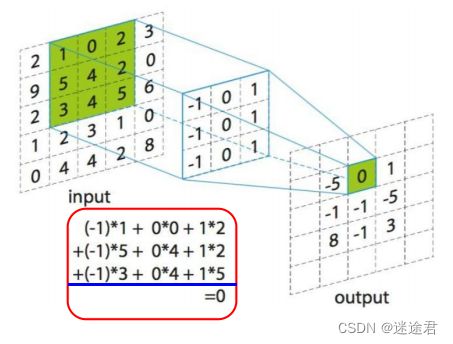
我们通过 卷积核( filter ) 与输入进行卷积运算, 提取局部特征 。卷积核从左到右对输入进行扫 描,每次滑动1格(步长为1),下图为滑动一 次后,卷积核每个元素和输入中绿色框相应位 置的元素 相乘后累加 ,得到输出中绿色框中的0。 扫描一次得到的就是特征值输出。
透过卷积结果图片,不难发现训练图片的明暗分解被表现出来了,卷积核提取到了图片中的特征。 上述例子只是单单一个卷积核,而当多层滤波器,数以万计的权重参数组合起来后,就可以达到检测出复杂图片中那些复杂特征了。
激活层
对卷积层的输出进行一个 非线性映射 , 更好的控制阈值,因为卷积计算是一种线性计算。常见的激活函数有relu、tanh、sigmoid 等,一般使用relu,使用relu求导明显会比tanh和sigmoid简单,可以减少计算量,同时, 使用tanh和sigmoid,当层数较多时容易导致梯度消失。
池化层
池化层:池化的目的就是减少特征图的维度,减少数据的运算量, 突出特征 。池化层是在卷积层之后,对卷积的输出, 进行池化运算。这样不会有可能损失了一些重要特征吗?这是因为图像数据在连续区域具有相关性,一般局部区域的 像素值差别不大 。比如眼睛的局部区域的像素点的值差别并不大,故我们使用Maxpooling或者MeanPooling并不会 损失很多特征
 卷积神经网络模型来识别我们的手写数字:
卷积神经网络模型来识别我们的手写数字:
在过程中我们需要不断调整我们的参数(比如卷积核个数大小,每次训练的数据个数,训练次数,以及学习步长等等都会影响我们的模型准确度),来使我们的损失函数值到达一个比较低的数值来保证我们预测的准确性
from keras.datasets import mnist
import matplotlib.pyplot as plt
from keras import Sequential
# 普通层 Dense, 卷积层Conv2D,最大池化层 Maxpooling2D,丢失Dropout,数据一维化
from keras.layers import Dense, Conv2D, MaxPooling2D, Dropout, Flatten
from keras.optimizers import Adam
from keras.utils import to_categorical
def load_data():
# load_data返回元组类型,顺序如下(x_train, y_train), (x_test, y_test)
(x_train, y_train), (x_test, y_test) = mnist.load_data()
print(x_train.shape, x_test.shape) # (60000,28,28)表示图片宽高28*28,60000/3=20000张
# plt.imshow(x_train[0])
# plt.show()
# 改变训练集图片的维度:最后的1表示灰度图,由于灰度图数值在0-255之间,所以要处理一下
# 改变之后变成(60000,28,28,1)
x_train = x_train.reshape(x_train.shape[0], x_train.shape[1], x_train.shape[2], 1).astype("float")/255
x_test = x_test.reshape(x_test.shape[0], 28, 28, 1).astype("float")/255
return (x_train, y_train), (x_test, y_test)
def modelCreate():
model1 = Sequential()
# 添加卷积层
# filters:卷积核个数 kernel_size:卷积核大小 input_shape:输入数据的维度
model1.add(Conv2D(filters=32, kernel_size=(5, 5), input_shape=(28, 28, 1), activation="relu"))
# 添加池化层 pool_size=(2, 2),池化大小为2*2
model1.add(MaxPooling2D(pool_size=(2, 2)))
# 防止特征数据被过度拟合,可以丢弃一部分数据
model1.add(Dropout(0.1))
# 再次添加卷积层
model1.add(Conv2D(filters=128, kernel_size=(5, 5), input_shape=(28, 28, 1), activation="relu"))
# 再次添加池化层 pool_size=(2, 2),池化大小为2*2
model1.add(MaxPooling2D(pool_size=(2, 2)))
# 防止特征数据被过度拟合,可以丢弃一部分数据
model1.add(Dropout(0.1))
# 数据一维化
model1.add(Flatten())
# 添加全连接层收拢数据,但不能一次性收拢
model1.add(Dense(units=1024, activation="relu"))
model1.add(Dense(units=256, activation="relu"))
model1.add(Dense(units=10, activation="softmax"))
adam = Adam(learning_rate=0.005)
model1.compile(optimizer=adam, loss="categorical_crossentropy")
return model1
def model_fit(model1, xx, yy):
# 因此要对标签集的数据进行one-hot编码
yy = to_categorical(yy, num_classes=10)
# fit函数:进行模型训练
# batch_size:每轮训练的数据个数
# epochs: 训练的轮次 verbose:2表示最后一轮打印相关信息,1表示每一轮打印相关信息,0表示不打印
model1.fit(xx, yy, batch_size=1000, epochs=10, verbose=1)
print(yy)
def model_evaluate(model1, xx, yy):
yy = to_categorical(yy, num_classes=10)
cost = model1.evaluate(xx, yy)
print("cost: ", cost)
if __name__ == "__main__":
# 获取数据集和标签集
(x_train, y_train), (x_test, y_test) = load_data()
# 搭建卷积神经网络
model = modelCreate()
# 机器深度学习,得到模型
model_fit(model, x_train, y_train)
# 模型评估
model_evaluate(model, x_test, y_test)
# 预测,predict_classes多分类预测
pre = model.predict_classes(x_test)
print("预测:", pre)
print("真实: ", y_test)
count = 0
for i in range(len(pre)):
if pre[i] != y_test[i]:
count += 1
print("错误:", count)
# 保存模型
model.save("num.xml")
随后我们将利用生成的模型来检测我们模型的准确率是否能够正确识别出我们手写数字的图片:
import cv2
from keras.models import load_model
# 加载本地模型
model = load_model("num.xml")
# 打开本地手写数字图片
img = cv2.imread("6.png")
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 改变图片的尺寸
img = cv2.resize(img, (28, 28))
img = img.reshape(1, 28, 28, 1).astype("float")/255
pre = model.predict_classes(img)
print("数字:", pre)