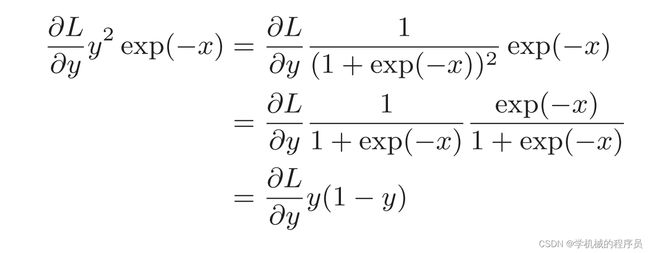BP神经网络的全过程简单实现（MATLAB实现，不调用已有的库，自己实现正向传播、反向传播等操作过程）

BP神经网络

该神经网络实现采用三层网络结构，结构如下图所示：

输入层节点数为1，隐藏层节点数为4，输出层节点数为1

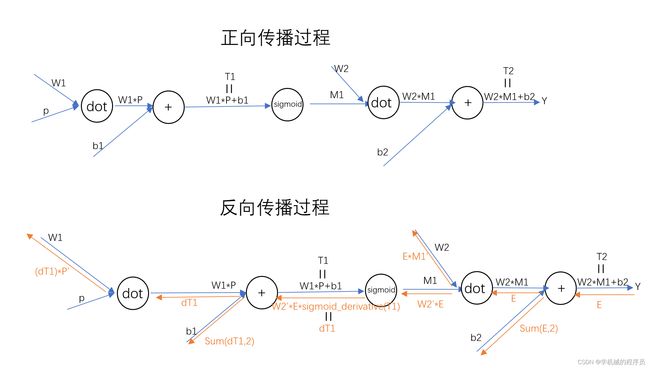
在神经网络实现过程中，核心部分是正向传播和反向传播的实现。下图是正向传播与反向传播的过程图。在看正向传播和反向传播过程之前，先看下面这个例子，能够帮助我们理解这个过程。

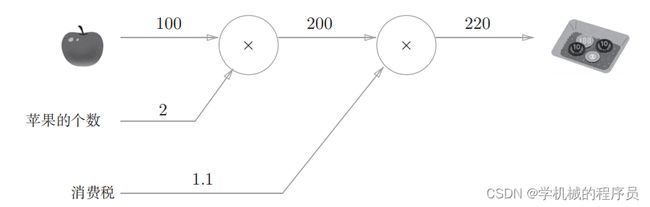
问题：太郎在超市买了2个100日元一个的苹果，消费税是10%，请计

算支付金额。

我们计算了购买2个苹果时加上消费税最终需要支付的金额。这里，假设我们想知道苹果价格的上涨会在多大程度上影响最终的支付金额，即求“支付金额关于苹果的价格的导数”。设苹果的价格为x，支付金额为L，则相当于求φL/φx 。这个导数的值表示当苹果的价格稍微上涨时，支付金额会增加多少。在实现神经网络的过程中我们就是要求当权重和偏置发生微小变化的时候目标输出与实际输出的误差会改变多少。

反向传播从右向左传递导数的值（1 → 1.1 → 2.2）。从这个结果中可知，“支付金额关于苹果的价格的导数”的值是2.2。这意味着，如果苹果的价格上涨1日元，最终的支付金额会增加2.2日元（严格地讲，如果苹果的价格增加某个微小值，则最终的支付金额将增加那个微小值的2.2倍）。这里只求了关于苹果的价格的导数，不过“支付金额关于消费税的导数”“支付金额关于苹果的个数的导数”等也都可以用同样的方式算出来。

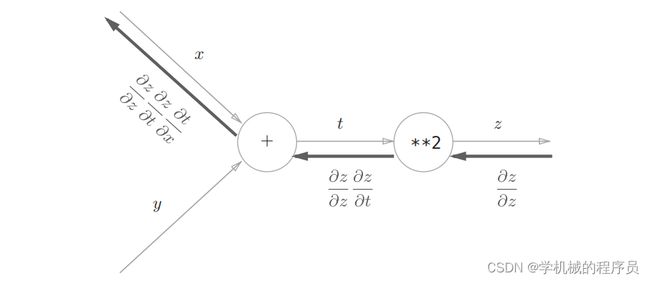
反向传播：

如图所示，计算图的反向传播从右到左传播信号。反向传播的计算顺序是，先将节点的输入信号乘以节点的局部导数（偏导数），然后再传递给下一个节点。比如，反向传播时，“**2”节点的输入是φz/φx ，将其乘以局部导数 φz/φt（因为正向传播时输入是t、输出是z，所以这个节点的局部导数是φz/φt ），然后传递给下一个节点。

在传递到下一个节点的时候要观察圆圈内的符号。

如果是+号，则不用改变直接传递。

如果是×号，要将值进行‘翻转’。

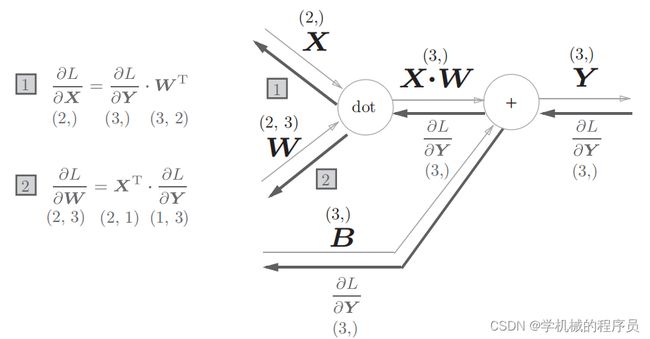
如果是dot,这里dot就是矩阵乘法。

如果是sigmoid,反向传播实现是sigmoid(x)*(1-sigmoid(x))。

这里只是简单地介绍了以下，如果觉得理解还是比较困难的话，可以参考《深度学习入门：基于Python的理论与实现》这篇文章，这篇文章本身就是一个从底层实现一个神经网络，并且在实现过程中他利用了许多通俗易懂的例子来帮助读者理解。你可以阅读其中的第五章 误差反向传播，你会对下面的传播过程有很清晰的理解。其中这篇文章中还讲解了损失函数（sigmoid函数）、梯度法（梯度下降法、梯度上升法）等其他神经网络的知识。

代码实现：

clc;
clear all;

%输入变量
P=[0,1,2,3,4,5,6,7,8,9,10];

%目标输出
T=[0,1,2,3,4,3,2,1,2,3,4];

%设置网络结构
input_size=1; %输入层大小
hide_size=4; %隐藏层大小
output_size=1; %输出层大小

%设置权重和偏置
W1=rand(hide_size,input_size);%输入层到隐藏层的权重
b1=rand(hide_size,1);%输入层到隐藏层的偏置
W2=rand(output_size,hide_size);%隐藏层到输出层的权重
b2=rand(output_size,1);%隐藏层到输出层的偏置

%设置训练次数、学习率和误差目标
train_iter=100000;
lr=0.01;
goal=0.01;

%开始训练
for t=1:train_iter
    %前向传播
    T1=W1*P+b1;
    M1=sigmoid(T1);%为什么要把值转化为这样的形式呢？举个例子，有100个 预测出正确的30个 然后稍微改一下权重和参数
    %还可能是预测出30个，这样电脑就不知道该往哪个方向调了，如果只是通过值来观察，当微小的改变权重参数的时候,
    % 这个值变化基本没什么反应，如果有反应，他的值也是不连续的、突然变化的。
    % 而sigmoid是0-1之间连续的函数，并且他的倒数不会为0，稍微改变权重的时候，他的值也会发生连续性的变化。
    T2=W2*M1+b2;
    Y=T2;%每训练一次得到的输出结果

    %计算每一次的误差
    E=Y-T;
    cost = sum(E.^2) / numel(T);%每一次的平均误差，为什么要这样呢？因为有些误差可能是负数，所以通过平方。

    %反向传播
    dT2=E;
    db2=sum(dT2,2);
    dW2=E*M1';
    dT1=W2'*E.*sigmoid_derivative(T1);
    db1=sum(dT1,2);
    dW1=dT1*P';

    %更新权重和偏置
    W1=W1-lr*dW1;
    b1=b1-lr*db1;
    W2=W2-lr*dW2;
    b2=b2-lr*db2;

    %展示训练的误差，这里每100次，显示一次误差
    if mod(t,100)==0
        fprintf('迭代次数：%d，训练误差：%f\n', t, cost);
    end

    %判断是否达到想要的误差精度
    if cost         fprintf('训练完成，迭代次数：%d，训练误差：%f\n', t, cost);
        break;%既然已经达到预期精度就不用再做循环了
    end

end

%将训练完成的权重和偏置带入，得到最终的输出
T1=W1*P+b1;
M1=sigmoid(T1);
T2=W2*M1+b2;
disp(['训练后的输出为',num2str(T2)]);

%训练完成后，查看预测输出和目标输出的差别
semilogy(T,'b:o')%目标输出
hold on
semilogy(T2,'r:o')%训练输出
xlabel('输入');
ylabel('输出');
legend('目标输出', '训练输出');

function y=sigmoid(x)
    y=1./(1+exp(-x));
end

function y=sigmoid_derivative(x)
    y=sigmoid(x).*(1-sigmoid(x));
end

结果展示：