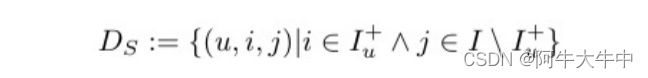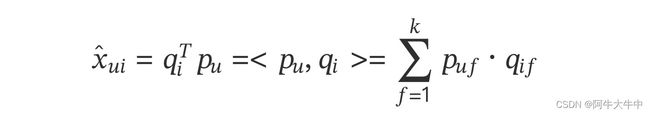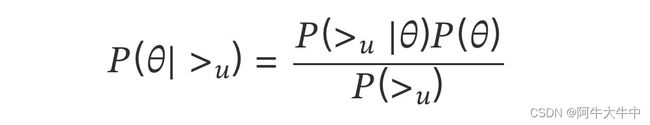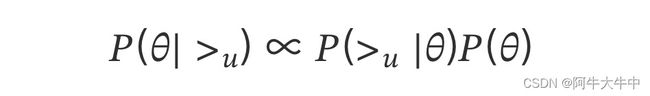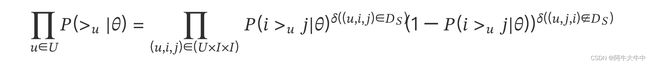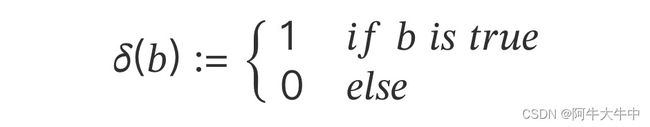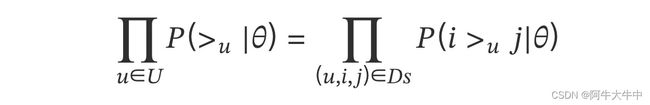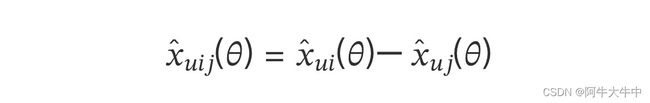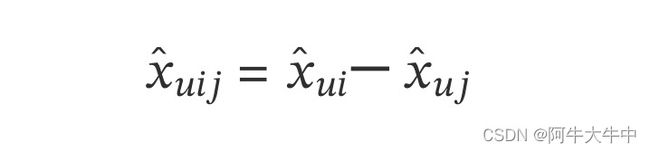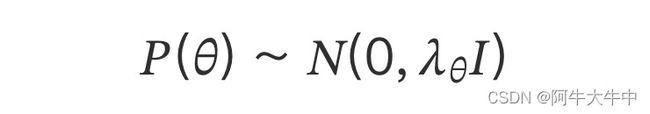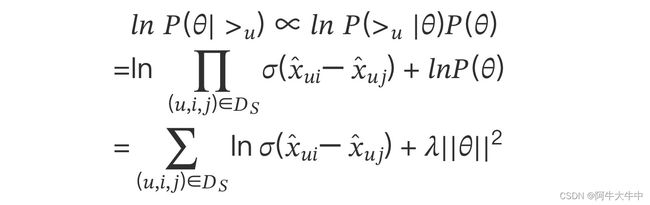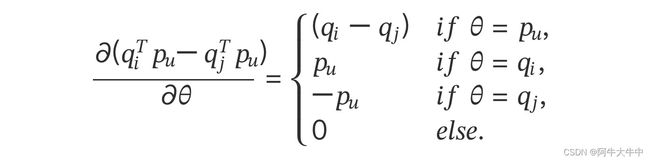推荐常用的排序学习算法——BPR（贝叶斯个性化排序）

本文是在学习SLEFRec项目的时候，其中的MF模型用的的方法是BPR（贝叶斯个性化排序），所以来学习一下，记录一下笔记。

1. 排序学习

在推荐算法中，排序学习（Learning to Rank，LTR）是一个重要的技术，用于确定推荐系统中给用户推荐物品的排序顺序。排序学习的目标是通过机器学习方法，将候选物品进行排序，以便将最相关和最有吸引力的物品展示给用户。

在排序学习中，通常使用的是有监督学习方法。

• 首先，需要构建一个训练数据集，其中包含用户-物品对以及相应的排序顺序。
• 然后，可以使用各种机器学习算法，如逻辑回归、支持向量机（SVM）、决策树等，来训练排序模型。这些算法可以根据一些特征，如用户的历史行为、物品的属性等，学习到一个排序函数，用于预测用户对未见过物品的喜好程度。

排序学习的关键挑战之一是特征选择和构建。选择合适的特征可以提高排序模型的效果。常用的特征包括用户的个人信息、历史行为、社交网络关系等，以及物品的属性、标签等。此外，还可以考虑上下文信息，如时间、地理位置等，以提供更精准的推荐。

1.1 优势

传统的检索模型所考虑的因素并不多，主要是利用词频、逆文档频率和文档长度、文档重要度这几个因子来人工拟合排序公式，且其中大多数模型都包含参数，也就需要通过不断的实验确定最佳的参数组合，以此来形成相关性打分。这种方式非常简单高效，但是也同时存在很多问题：

1. 很难融合多种信息
2. 手动调参工作量太大，如果模型参数很多，手动调参的可用性非常低
3. 可能会过拟合

LTR 则是基于特征，通过机器学习算法训练来学习到最佳的拟合公式，相比传统的排序方法，优势有很多:

1. 可以根据反馈自动学习并调整参数
2. 可以融合多方面的排序影响因素
3. 避免过拟合（通过正则项）
4. 实现个性化需求（推荐）
5. 多种召回策略的融合排序推荐（推荐）
6. 多目标学习（推荐）

1.2 排序学习在推荐领域的作用

排序学习在推荐领域扮演着关键的角色，它的作用如下：

1. 个性化推荐：排序学习能够通过学习用户的兴趣和偏好，为每个用户生成个性化的推荐列表。通过将最相关和最吸引人的物品排在前面，排序学习可以提供与用户需求和兴趣高度匹配的推荐结果，从而提升用户满意度。
2. 提高推荐准确性：排序学习可以根据用户的历史行为和反馈信息，学习到一个排序模型，能够准确预测用户对未见过物品的喜好程度。通过有效的排序，推荐系统可以更准确地预测用户的兴趣，提供符合用户期望的推荐结果，提高推荐的准确性。
3. 优化推荐排序策略：排序学习可以通过机器学习方法，对推荐系统中的排序策略进行优化。通过学习用户的行为模式和反馈信息，排序学习可以发现隐藏的用户偏好和规律，从而改进排序算法，提供更精准和有效的推荐排序策略。
4. 多样性和平衡性：排序学习可以在推荐过程中考虑多个因素，如物品的多样性和平衡性。推荐系统可以通过排序学习来平衡推荐结果中的热门物品和长尾物品，确保推荐列表既包含热门物品以满足用户的主流需求，又包含长尾物品以满足用户的个性化需求。
5. 实时推荐：排序学习可以快速适应用户的实时行为和上下文信息，实现实时推荐。通过实时学习和排序，推荐系统可以根据最新的用户行为和环境变化，及时调整推荐排序，提供及时、准确的推荐结果。

总的来说，排序学习在推荐领域的作用是优化推荐结果的排序顺序，提供个性化、准确和满意度高的推荐体验。它能够改善推荐系统的性能，提升用户满意度，增加用户粘性，促进业务增长。

推荐的整个流程可以分为召回、排序、重排序这三个阶段，通俗来说，召回就是找到用户可能喜欢的几百条资讯，排序就是对这几百条资讯利用机器学习的方法预估用户对每条资讯的偏好程度，一般以点击率衡量，也就是点击率预估问题。不难看出，排序学习在推荐领域主要用于排序阶段，最常用的是 Pointwise 排序方法；重排序更多是考虑业务逻辑的规则过滤，如在推荐结果的多样性、时效性、新颖性等方面进行控制。

在没有 Learning to Rank 之前，基于内容的推荐算法和基于邻域的协同过滤虽然也能预测用户的偏好，可以帮助用户召回大量的物品，但是我们必须知道，推荐系统中更重要的目标是排序，因为真正最后推荐给用户的只有少数物品，我们更关心这些召回物品中哪些才是用户心中更加喜欢的，也就是排序更靠前，这便是 Top-N 推荐。

1.3 排序学习设计思路

排序学习的模型通常可以分为单点法（Pointwise Approach）、配对法（Pairwise Approach）和列表法（Listwise Approach）三大类。这些方法针对排序问题的不同方面进行建模和处理。

1. 单点法（Pointwise Approach）： 单点法是一种简单直接的排序学习方法，它将排序问题转化为一个回归或分类问题，通过对每个样本进行独立的预测和排序。在单点法中，每个样本都被视为一个独立的实例，模型的输入是样本的特征，输出是预测的排序分数或概率。常见的单点法模型包括逻辑回归、线性回归、支持向量机等。单点法的优点是简单、易于实现，但它忽略了物品之间的相互关系和排序的整体性。
2. 配对法（Pairwise Approach）： 配对法通过比较和排序样本中的配对来进行排序学习。它关注的是物品之间的相对顺序，而不仅仅是单个样本的排序分数。在配对法中，模型的输入是一对物品的特征差异，输出是判断哪个物品更适合排在前面的分数。通过学习配对之间的相对排序，可以更好地处理排序问题。常见的配对法模型包括RankNet、RankBoost、RankSVM等。
3. 列表法（Listwise Approach）： 列表法是一种直接优化排序列表的方法，它考虑了整个列表的排序顺序。列表法模型直接建模并最大化真实排序顺序的可能性。在列表法中，模型的输入是一组物品的特征，输出是对这组物品的排序得分。列表法可以通过最大化排序指标（如NDCG、MAP等）来优化整个排序列表的质量。常见的列表法模型包括LambdaRank、ListNet、ListMLE等。

这三种方法各有特点，适用于不同的排序场景和问题。单点法简单直接，适用于简单排序问题；配对法考虑物品之间的相对顺序，适用于处理排序差异大的样本；列表法直接优化整个排序列表，适用于追求整体排序质量的场景。根据实际情况和需求，可以选择合适的排序学习方法来解决推荐排序问题。

1.3.1 单点法（Pointwise）

Pointwise方法是排序学习中的一种常见方法，也称为单点法。它将排序问题转化为一个回归或分类问题，通过对每个样本进行独立的预测和排序。

在Pointwise方法中，每个样本都被视为一个独立的实例，模型的输入是样本的特征，输出是预测的排序分数或概率。具体步骤如下：

1. 数据准备：首先，需要准备带有特征和排序标签的训练数据集。每个样本包含一个物品的特征向量和对应的排序标签。特征可以包括用户的历史行为、物品的属性、上下文信息等。排序标签可以是实际的排序值，也可以是代表排序关系的类别。
2. 特征表示：对于每个物品，将其特征表示为一个向量。特征向量可以根据实际情况选择不同的表示方法，如基于内容的特征、用户行为特征、协同过滤特征等。
3. 模型选择与训练：选择适合的模型来建立特征和排序标签之间的映射关系。常见的模型包括逻辑回归、线性回归、支持向量机等。根据训练数据集，通过最小化损失函数，学习模型的参数和权重。优化方法可以使用梯度下降等常见的优化算法。
4. 预测与排序：使用训练好的模型对测试样本进行预测和排序。对于每个测试样本，输入其特征向量到模型中，得到预测的排序分数或概率。根据预测结果，对物品进行排序，将得分高的物品排在前面。
5. 模型评估：使用评估指标来评估模型的性能。常用的指标包括精确度、召回率、均方根误差（RMSE）等。通过与真实的排序标签进行比较，评估模型的排序准确性和性能。

Pointwise方法的优点在于：

简单、直接，并且易于实现。它适用于简单的排序问题，特别是当物品之间的差异较小，且样本的数量较大时，可以取得不错的结果。

然而，Pointwise方法忽略了物品之间的相对顺序和排序的整体性，可能无法充分利用物品之间的关系和排序的结构信息。在一些复杂的排序问题中，配对法（Pairwise Approach）和列表法（Listwise Approach）通常更加适用，可以更好地处理排序问题。

1.3.2 配对法（Pairwise）

Pairwise方法是排序学习中的一种常见方法，也被称为配对法。它通过比较和排序样本中的配对来进行排序学习，关注物品之间的相对顺序，而不仅仅是单个样本的排序分数。

在Pairwise方法中，模型的输入是一对物品的特征差异，输出是判断哪个物品更适合排在前面的分数。具体步骤如下：

1. 数据准备：与Pointwise方法类似，需要准备带有特征和排序标签的训练数据集。不同的是，Pairwise方法中的排序标签表示两个物品之间的相对排序关系，通常用1和0表示。例如，1表示第一个物品应该排在前面，0表示第二个物品应该排在前面。
2. 特征表示：与Pointwise方法相同，对每个物品将其特征表示为一个向量。特征向量可以根据实际情况选择不同的表示方法。
3. 构造配对：为了训练Pairwise模型，需要从训练数据中构造配对样本。对于每个样本，从中选择两个不同的物品进行配对，并标记其相对排序关系。可以根据排序标签构建配对样本，如对于一个排在前面的物品，将其与后面的物品进行配对。
4. 模型选择与训练：选择适合的模型来建立特征差异和排序标签之间的映射关系。常见的模型包括RankNet、RankBoost、RankSVM等。这些模型通过学习特征差异的权重和模型的参数，能够捕捉到物品之间的排序关系。
5. 预测与排序：使用训练好的模型对测试样本进行预测和排序。对于每个测试样本，计算两个物品的特征差异，输入到模型中得到相对排序的分数。根据分数，对物品进行排序。
6. 模型评估：使用评估指标来评估模型的性能，如精确度、召回率、均方根误差（RMSE）等。通过与真实的相对排序标签进行比较，评估模型的排序准确性和性能。

Pairwise方法相比于Pointwise方法，更加关注物品之间的相对排序关系，能够更好地处理排序问题。它通过比较配对样本中的物品，学习到它们之间的相对排序偏好。

优点：

1. 利用了物品之间的相对排序信息：Pairwise方法可以通过比较和排序样本中的配对，学习到物品之间的相对排序偏好。相比于Pointwise方法，更能够捕捉到物品之间的差异和排序关系。
2. 更适应排序差异大的样本：在一些排序问题中，不同物品之间的排序差异可能很大。Pairwise方法可以通过比较配对样本中的物品，更加灵活地处理这种排序差异，对排序结果更具有区分能力。
3. 相对较为简单：相比于列表法（Listwise Approach），Pairwise方法的训练过程较为简单。它将排序问题转化为二分类或回归问题，可以使用常见的机器学习算法进行模型训练。

缺点：

1. 需要构造配对样本：Pairwise方法需要从训练数据中构造配对样本，将原始的排序标签转化为相对排序关系。这会增加训练样本的数量，并且需要更多的计算资源和时间。
2. 无法全局优化排序列表：与列表法相比，Pairwise方法只关注配对之间的相对排序关系，而无法直接优化整个排序列表的质量。它可能无法捕捉到整体排序结构中的复杂模式和关联信息。

常见的Pairwise方法包括RankNet、RankBoost和RankSVM等。这些方法通过学习特征差异的权重和模型参数，可以建模物品之间的相对排序偏好。它们在推荐系统和信息检索等领域得到了广泛应用，并取得了良好的排序效果。

Pairwise方法能够更好地处理物品之间的相对排序关系，相比于Pointwise方法能够充分利用样本中的排序信息。然而，Pairwise方法需要构造配对样本，会增加训练样本的数量，并且计算复杂度也相对较高。在一些复杂的排序问题中，列表法（Listwise Approach）通常更适用，可以直接优化整个排序列表的质量。

1.3.3 列表法（Listwise）

Listwise方法是排序学习中的一种常见方法，也被称为列表法。它直接优化整个排序列表的质量，考虑了整体排序顺序，相比于Pointwise和Pairwise方法，更加全面和综合地处理排序问题。

在Listwise方法中，模型的输入是一组物品的特征向量，输出是对这组物品的排序得分。具体步骤如下：

1. 数据准备：与其他排序方法类似，需要准备带有特征和排序标签的训练数据集。每个样本由一组物品的特征向量和对应的排序标签组成。
2. 特征表示：对每个物品，将其特征表示为一个向量，可以根据实际情况选择不同的表示方法。
3. 列表建模：选择适合的列表法模型来建立特征向量和排序标签之间的映射关系。常见的列表法模型包括LambdaRank、ListNet、ListMLE等。
4. 模型训练：通过最大化排序指标（如NDCG、MAP等）或最小化损失函数来优化模型的参数和权重。优化方法可以使用梯度下降等常见的优化算法。
5. 预测与排序：使用训练好的模型对测试样本进行预测和排序。对于每个测试样本，输入一组物品的特征向量到模型中，得到预测的排序得分。根据得分，对物品进行排序。
6. 模型评估：使用评估指标来评估模型的性能，如NDCG、MAP等。通过与真实的排序标签进行比较，评估模型的排序准确性和性能。

Listwise方法的优点在于直接优化整个排序列表的质量，考虑了物品之间的全局排序关系。相比于Pointwise和Pairwise方法，Listwise方法能够更好地捕捉到整体排序结构中的复杂模式和关联信息。

然而，Listwise方法也面临一些挑战和限制。由于需要直接优化整个排序列表，Listwise方法的训练和优化过程相对复杂，计算复杂度较高。此外，Listwise方法对于大规模数据集和高维特征空间可能存在一定的挑战。

尽管如此，Listwise方法在推荐系统、搜索引擎和广告排序等领域仍然得到广泛应用，并且在提高排序质量和用户体验方面具有显著效果。

Listwise方法是排序学习中最为综合和全面的方法之一，它通过直接优化整个排序列表的质量来解决排序问题。相比于Pointwise和Pairwise方法，Listwise方法能够更充分地利用排序列表的结构信息，提高排序的准确性和效果。

Listwise方法的特点如下：

1. 全局排序优化：Listwise方法直接优化整个排序列表的质量，而不是仅考虑单个样本或配对之间的排序关系。它能够捕捉到整体排序结构中的复杂模式和关联信息，提供更准确和一致的排序结果。
2. 考虑序列特征：由于Listwise方法关注整个排序列表，它可以自然地考虑序列特征的影响。例如，在推荐系统中，用户的历史行为序列可以被编码为排序列表，通过Listwise方法可以更好地建模序列中的物品关系和用户偏好。
3. 评估指标一致性：Listwise方法通常使用排序相关的评估指标（如NDCG、MAP等）来优化模型，这些指标与实际排序质量直接相关。通过直接优化这些指标，Listwise方法可以在排序准确性上取得更好的性能。
4. 模型多样性：Listwise方法可以使用不同的模型来进行排序列表的优化。常见的Listwise方法包括LambdaRank、ListNet、ListMLE等。这些方法在损失函数、模型结构和训练算法上存在差异，可以根据具体问题选择适合的模型。

2. BPR（贝叶斯个性化推荐）

BPR（Bayesian Personalized Ranking）算法是一种常用的排序学习算法，通过建模个性化排序问题来进行推荐。它基于概率模型，通过最大化物品排名的后验概率来学习用户对物品的偏好。尽管BPR算法存在一些限制，但它在大规模数据集和高维特征空间中具有优势，并在推荐系统中得到广泛应用。

BPR算法的核心思想是将排序问题转化为二分类问题，通过比较用户对两个物品的偏好来建立排序模型。具体步骤如下：

1. 数据准备：BPR算法的训练数据包括用户对物品的隐式反馈数据，例如用户的点击、购买或评分行为。每个样本由用户ID、正样本（用户有过行为的物品）和负样本（用户没有行为的物品）组成。
2. 特征表示：对每个用户和物品，需要将其表示为特征向量。特征向量可以包括基于内容的特征、用户和物品的属性等。常见的表示方法包括使用词袋模型、嵌入表示或其他特征工程方法。
3. 模型建立：BPR算法使用矩阵分解方法来学习用户和物品的潜在特征向量。它假设用户和物品的特征向量可以通过低维的潜在因子进行表示。通常使用随机梯度下降（Stochastic Gradient Descent, SGD）等方法进行模型训练。
4. 采样配对：在每次训练迭代中，从训练数据中随机选择一个用户-物品-负样本配对。这样可以构造用户对正样本和负样本的比较关系，用于模型的训练。
5. 模型训练：BPR算法通过最大化物品排名的后验概率来优化模型的参数。具体来说，它通过随机梯度下降法（SGD）来最大化样本对的对数似然函数，从而学习用户和物品的潜在特征向量。
6. 预测与排序：使用训练好的模型对测试数据进行预测和排序。对于每个用户，计算其与未曾交互的物品的得分，根据得分进行排序，推荐排名靠前的物品。

BPR算法有以下的限制：

1. 无法处理缺乏隐式反馈的情况：BPR算法主要依赖于用户的隐式反馈数据，如点击、购买或评分等行为。对于缺乏这些隐式反馈数据的情况，BPR算法无法直接应用。介绍显示反馈与隐式反馈。
2. 未考虑物品之间的相关性：BPR算法只关注用户对单个物品的偏好，而忽略了物品之间的相关性。在某些场景下，物品之间的相关性对于排序结果的影响可能很重要，但BPR算法未对其进行建模。
3. 未考虑用户的上下文信息：BPR算法主要关注用户和物品的特征，而忽略了用户的上下文信息，如时间、地点、环境等。在某些场景下，用户的上下文信息对排序结果具有重要影响，但BPR算法未对其进行建模。

2.1 BPR算法使用背景

在很多推荐场景中，我们都是基于现有的用户和商品之间的一些数据，得到用户对所有商品的评分，选择高分的商品推荐给用户，这是funkSVD之类算法的做法，使用起来也很有效。但是在有些推荐场景中，我们是为了在千万级别的商品中推荐个位数的商品给用户，此时，我们更关心的是用户来说，哪些极少数商品在用户心中有更高的优先级，也就是排序更靠前。也就是说，我们需要一个排序算法，这个算法可以把每个用户对应的所有商品按喜好排序。BPR就是这样的一个我们需要的排序算法。

2.2 BPR算法相关定义

U代表所有用户user集合；I代表所有物品item集合；S代表所有用户的隐式反馈。

可知，⊆×。

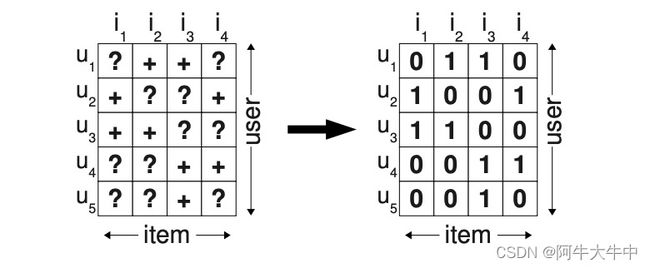
如下图所示，只要用户对某个物品产生过行为（如点击、收藏、加入购物车等），就标记为+，所有+样本构成了S。那些为观察到的数据（即用户没有产生行为的数据）标记为？。

因为是基于贝叶斯的 Pairwise 方法，BPR 有两个基本假设：

1. 一是每个用户之间的偏好行为相互独立，即用户u在商品i和j之间的偏好和其他用户无关。
2. 二是同一用户对不同物品的偏序相互独立，也就是用户u在商品i和j之间的偏好和其他的商品无关。

在原始论文中，BPR 用来解决隐式反馈的推荐排序问题，假设有用户集 U 和物品集 I，当用户 u（∈）在物品展示页面点击了物品 i（∈）却没有点击同样曝光在展示页面的物品 j（∈），则说明对于物品 i 和物品 j，用户 u 可能更加偏好物品 i，用 Pairwise 的思想则是物品 i 的排序要比物品 j 的排序更靠前，这个偏序关系可以写成一个三元组 <,,>，为了简化表述，我们用 > 符号表示用户 u 的偏好，<,,> 可以表示为：>。单独用 > 代表用户 u 对应的所有商品中两两偏序关系，可知 >⊂2，且 > 满足下面的特性：

• 完整性：∀,∈:≠⇒>∪>
• 反对称性：∀,∈:>∩>⇒=
• 传递性：∀,,∈:>∩>⇒>

记 S 为所有用户对所有物品发生的隐式反馈集合，这里针对隐式反馈问题对评分矩阵进行了简化，即点击过则视为正例，记为 1；没点击过则视为负例，通常会置为 0，如下图所示：

对该数据进行模型拟合。这意味着该模型被优化为预测S中元素的值为1，其余元素的值为0。这种方法的问题在于，在训练过程中，模型未来应该排序的所有元素((U ×I) \ S)都以负反馈的形式呈现给学习算法。这意味着一个具有足够表达能力(可以精确拟合训练数据)的模型根本无法排序，因为它预测的只是0。这种机器学习方法能够预测排名的唯一原因是防止过拟合的策略，比如正则化。

我们知道，矩阵分解是通过预测用户对候选物品的评分，然后根据这个预测评分去排序，最后再推荐给用户。这种方法是一种典型的 Pointwise 方法，无论是预测评分还是预测隐式反馈，本质上都是在预测用户对一个物品的偏好程度。

但是这种方法有很大的问题，因为很多时候我们只能收集到少数正例样本，剩下的数据其实是真实负例和缺失值的混合构成（这里的缺失值是指训练数据中除正例和负例外的未知数据，可以理解为未曝光或者曝光了的但是用户可能没有注意到缺失数据，所以缺失值中的样本即有可能是正例，也有可能是负例），而我们用这种方法构建训练数据的时候，往往无法确定负例到底是哪些，就只能把除正例以外的其他部分都当作是负例，这就会使得训练数据中负例的一部分其实是缺失值。把缺失值当作是负样本，再以预测误差为评判标准去使劲逼近这些样本。逼近正样本没问题，但是同时逼近的负样本只是缺失值而已，真正呈现在用户面前，并不能确定是不喜欢还是喜欢。而且，这样的模型仅能预测正例或负例，对于类别内的样本无法深入区别其重要性，不利于排序。

当然，对于这种情况，我们也可以用一些其他方法来规避这些问题，比如负例采样，比如按预测概率排序，但这些方法也仅仅是 “缓兵之计”，对于解决排序问题来说并不完善。

2.3 BPR样本构建

我们使用了一种不同的方法，使用项目对作为训练数据，并对正确排名项目对进行优化，而不是对单个项目进行评分，因为这比仅仅用负值替换缺失值更好地代表了问题。从S开始，我们尝试为≻u的每个用户部分进行重构。如果一个项目i被用户u浏览过——即:(u, i)∈S -那么我们假设用户更喜欢这个项目而不是其他所有未观察到的项目。例如，在下图中，用户u1看过物品i2，但没有看过物品i1，所以我们假设这个用户喜欢物品i2胜过物品i1: i2 ≻u i1。对于两个都被用户看到的物品，我们无法推断出任何偏好。对于用户尚未见过的两个项目也是如此(例如，用户u1)的项目i1和i4。为了形式化，我们通过以下方式创建训练数据DS:U ×I ×I:

其中 (,,)∈ 的表示是用户 u 更喜欢 i 胜过 j；∧ 是离散数学中的符号，表示 and，等同于 ∩；∖+ 表示物品集 除正例外其他剩余的样本。

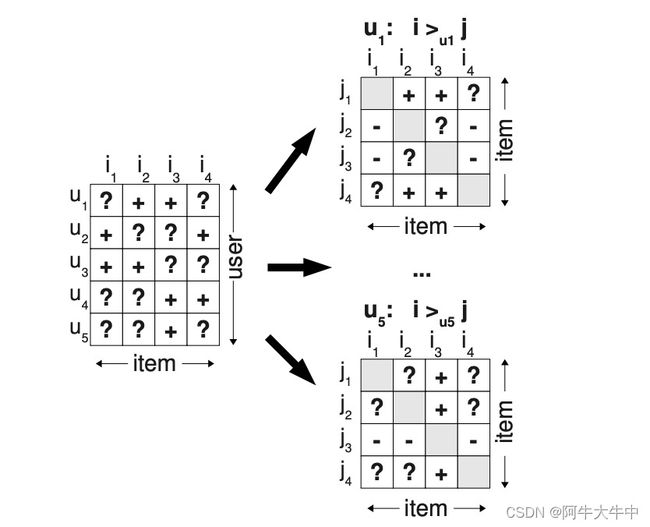
首先 BPR 利用 Pairwise 的思想来构建偏序关系，它依然没有从无反馈数据中去区分负例样本和缺失值，不过和之前的方法不一样的是，BPR 不是单纯地将无反馈数据都看做是负例，而是与正例结合一起来构建偏序关系。这里的核心假设是，某用户对他有过反馈的物品的偏好程度一定比没有反馈过的物品高（这里的反馈一般指隐式反馈，如点击浏览等，不涉及负反馈），未反馈的物品包括真正的负例以及缺失值。BPR 试图通过用户的反馈矩阵 S 来为每一个用户构建出完整的偏序关系，也称全序关系，用 > 表示。

图左边的矩阵是反馈数据集 S，+ 代表有反馈数据，? 代表无反馈数据。

图右边的小矩阵是每个用户的偏序关系矩阵，+代表用户喜欢 i 胜过喜欢 j，作为训练数据的正例；-代表用户喜欢 j 胜过喜欢 i，作为训练数据的负例；?代表同类数据无法确定偏序关系。

相比于单点法的矩阵分解，基于配对法的 BPR 有两大优势：

1. 训练数据由正样本，负样本和缺失值构成。两个未观测到的物品的缺失值正好就是以后需要进行排序的物品对。这意味着从成对训练的角度，训练数据 和测试数据是不相交的。
2. 训练数据是为后面的排序目标函数生成的，也就是观测值 > 的子集 被用作训练数据。

2.4 构建目标函数

通过上面的样本构造便可以得到我们的训练样本，每一个样本都是由用户 u、物品 i、物品 j、以及两个物品的偏序关系 y 构成的四元组 (,,,)，其中 y 表示两个物品偏序关系并作为 label，通常用 0、1 标注，如物品 i 的偏序大于物品 j 的，则 y 标注为 1，反之则标注为 0。

接下来我们来看看如何构建目标函数。

首先我们必须清楚，这回的目标不再是像 MF 的均方根误差最小，而是需要满足物品相对排序最佳。一个简单的思路就是当得到了用户和物品的推荐分数后，就可以计算四元组的样本中，物品 i 和物品 j 的分数差，这个分数可能是正数，也可能是负数，也可能是 0。

我们可以通过预测分数的差值的大小来判断排序是否良好，最希望的情况是：如果物品 i 和物品 j 偏序关系的标注为 1，那么希望两者分数之差是个正数，而且越大越好；如果物品 i 和物品 j 的相对顺序是 0，则希望分数之差是负数，且越小越好。

可以看出，这种方式来构建目标函数的话，依然是需要预测分数的，而这个分数的预测最常用的就是矩阵分解的方法，原论文中还用到了另外一种方法，叫自适应 K 近邻（Adaptive KNN）。这里我们这里只看矩阵分解。当然 BPR 中的预测的分数无论在显示反馈还是隐式反馈情境下，都只是用来辅助度量相对排序，其评分并不作为实际的意义上的评分。

同 FunkSVD 矩阵一样，预测分数 ̂ 的问题可以视作对矩阵进行估计 :×。通过矩阵分解我们可以将目标矩阵 X 近似分解为两个低秩矩阵 (||×) 和 (||×) 的乘积：

其中 是特征矩阵的维度。 中的每一行 可以视作描述一个用户的特征向量，类似地 中的每一行 可以视作描述物品 的特征向量。因此，预测公式也可以写成：

其中，⟨⋅,⋅⟩ 代表向量点积。

有了这些基础的理解后，接下来我们来看 BPR 如何在矩阵分解的基础上来构建排序的目标函数，BPR 的过程实际上是一种优化过程。

2.5 BPR损失函数推导

BPR 基于最大后验估计(,|>) 来求解模型参数 ,，这里我们用 来表示参数 和 ， > 代表用户 u 对应的所有商品的全序关系，则优化目标是 (|>)。根据贝叶斯公式，我们有：

由于我们求解假设了用户的排序和其他用户无关，那么对于任意一个用户 u 来说，(>) 对所有的物品一样，所以有：

这个优化目标转化为两部分。第一部分和样本数据集 有关，第二部分和样本数据集 无关。

对于第一部分，由于我们假设每个用户之间的偏好行为相互独立，同一用户对不同物品的偏序相互独立，所以有：

其中，

根据上面讲到的完整性和反对称性，优化目标的第一部分可以简化为：

而对于 (>|) 这个概率，我们可以使用下面这个式子来代替:

其中，() 是 sigmoid 函数，即：

这里你也许会问，为什么可以用这个 sigmoid 函数来代替呢? 其实这里的代替可以选择其他的函数，不过式子需要满足 BPR 的完整性，反对称性和传递性。原论文作者这么做除了是满足这三个性质外，另一个原因是为了方便优化计算。

对于 ̂ () 这个式子，我们要满足当 > 时，̂ ()>0, 反之当 > 时，̂ ()<0，最简单的表示这个性质的方法就是:

而 ̂ () , ̂ ()，就是我们的矩阵 ̂ 对应位置的值。这里为了方便，我们不写 ，这样上式可以表示为:

注意上面的这个式子也不是唯一的，只要可以满足上面提到的当 > 时，̂ ()>0，以及对应的相反条件即可。这里我们仍然按原论文的式子来。

最终，我们的第一部分优化目标转化为：

对于第二部分 ()，原作者大胆使用了贝叶斯假设，即这个概率分布符合正态分布，且对应的均值是 0，协方差矩阵是 , 即

后面我们做优化时，需要计算 ()，而对于上面假设的这个多维正态分布，其对数和 ||||2 成正比。即：

最终对于我们的最大对数后验估计函数:

由于

再添加负号以求最小损失，并将 拆分，由此我们便得到 BPR 最终的损失函数：

2.6 BPR的优化学习过程

BPR 可以用常用的梯度下降或者牛顿法来优化，我们以梯度下降为例:

对 求导：

这样我们可以求出：

2.7 BPR算法流程

下面简要总结下 BPR 的算法训练流程：

输入：训练集 D 三元组，学习率 ， 正则化参数 ，分解矩阵维度 k。

输出：模型参数，矩阵 P、Q

1. 随机初始化矩阵 P、Q
2. 迭代更新模型参数：

3. 如果 P、Q 收敛，则算法结束，输出 P、Q，否则回到步骤 2。

当我们拿到 P、Q 后，就可以计算出每一个用户 u 对应的任意一个商品的排序分：̂ =，最终选择排序分最高的若干商品输出。

2.8 BPR小结

BPR 其实可以看作在准确率之上更加高层的排序算法框架，可以将 Pointwise 变成 Pairwise，因此，实际上它不仅仅局限于矩阵分解，理论上 Pointwise 算法都可以使用 BPR，难点在于求损失函数。另外，基于 MF 的 BPR 经过了很好的验证，使用范围很广，所以但凡适用于 MF 的推荐场景，基本都可以在其上层添加 BPR 进行排序优化。

在实际产品中，BPR 之类的推荐排序在海量数据中选择极少量数据做推荐的时候有优势，因此在很多互联网大厂中应用也很广泛。

3. 代码实现

本代码使用ml-100k数据集进行训练与测试，提取出ml-100k数据集中评分高于4分的（满分5分）作为用户对该电影进行过标记（好印象）。

总共包含943个用户，1682部电影。

BPR主函数代码，BPR_basical.py：

import random
from collections import defaultdict
import numpy as np
from sklearn.metrics import roc_auc_score
import scores
'''
函数说明:BPR类（包含所需的各种参数）
Parameters:
    无
Returns:
    无
'''
class BPR:
    # 数据集为ml-100k选取用户评分高于4分的作为用户标记过的电影
    #用户数
    user_count = 943
    #项目数
    item_count = 1682
    #k个主题,k数
    latent_factors = 20
    #步长α
    lr = 0.01
    #参数λ
    reg = 0.01
    #训练次数
    train_count = 10000
    #训练集
    train_data_path = 'train.txt'
    #测试集
    test_data_path = 'test.txt'
    #U-I的大小
    size_u_i = user_count * item_count
    # 随机设定的U，V矩阵(即公式中的Puk和Qik)矩阵
    U = np.random.rand(user_count, latent_factors) * 0.01 #大小无所谓
    V = np.random.rand(item_count, latent_factors) * 0.01
    biasV = np.random.rand(item_count) * 0.01
    #生成一个用户数*项目数大小的全0矩阵
    test_data = np.zeros((user_count, item_count))
    # print("test_data_type",type(test_data))
    #生成一个一维的全0矩阵
    test = np.zeros(size_u_i)
    #再生成一个一维的全0矩阵
    predict_ = np.zeros(size_u_i)

    #获取U-I数据对应
    '''
    函数说明：通过文件路径，获取U-I数据
    Paramaters:
        输入要读入的文件路径path
    Returns:
        输出一个字典user_ratings，包含用户-项目的键值对
    '''
    def load_data(self, path):
        user_ratings = defaultdict(set)
        with open(path, 'r') as f:
            for line in f.readlines():
                u, i = line.split(" ")
                u = int(u)
                i = int(i)
                user_ratings[u].add(i)
        return user_ratings
    '''
    函数说明：通过文件路径，获取测试集数据
    Paramaters：
        测试集文件路径path
    Returns:
        输出一个numpy.ndarray文件（n维数组）test_data,其中把含有反馈信息的数据置为1
    '''
    #获取测试集的评分矩阵
    def load_test_data(self, path):
        file = open(path, 'r')
        for line in file:
            line = line.split(' ')
            user = int(line[0])
            item = int(line[1])
            self.test_data[user - 1][item - 1] = 1
    '''
    函数说明：对训练集数据字典处理，通过随机选取，（用户，交互，为交互）三元组，更新分解后的两个矩阵
    Parameters：
        输入要处理的训练集用户项目字典
    Returns：
        对分解后的两个矩阵以及偏置矩阵分别更新
    '''
    def train(self, user_ratings_train):
        for user in range(self.user_count):
            # 随机获取一个用户
            u = random.randint(1, self.user_count) #找到一个user
            # 训练集和测试集的用户不是全都一样的,比如train有948,而test最大为943
            if u not in user_ratings_train.keys():
                continue
            # 从用户的U-I中随机选取1个Item
            i = random.sample(user_ratings_train[u], 1)[0] #从随机获取的用户u的评分列表中，找到一个被评分item
            # 随机选取一个用户u没有评分的项目
            j = random.randint(1, self.item_count)
            while j in user_ratings_train[u]:
                j = random.randint(1, self.item_count) #从所有电影item列表中，找到一个没有被用户u评分过的item，这样可以保证用户u更加偏好物品i
            #构成一个三元组（uesr,item_have_score,item_no_score)
            # python中的取值从0开始
            u = u - 1
            i = i - 1
            j = j - 1
            #BPR
            r_ui = np.dot(self.U[u], self.V[i].T) + self.biasV[i] # .T表示将原来的向量转置
            r_uj = np.dot(self.U[u], self.V[j].T) + self.biasV[j]
            r_uij = r_ui - r_uj
            loss_func = -1.0 / (1 + np.exp(r_uij))
            # 更新2个矩阵
            self.U[u] += -self.lr * (loss_func * (self.V[i] - self.V[j]) + self.reg * self.U[u])
            self.V[i] += -self.lr * (loss_func * self.U[u] + self.reg * self.V[i])
            self.V[j] += -self.lr * (loss_func * (-self.U[u]) + self.reg * self.V[j])
            # 更新偏置项
            self.biasV[i] += -self.lr * (loss_func + self.reg * self.biasV[i])
            self.biasV[j] += -self.lr * (-loss_func + self.reg * self.biasV[j])
    '''
    函数说明：通过输入分解后的用户项目矩阵得到预测矩阵predict
    Parameters:
        输入分别后的用户项目矩阵
    Returns：
        输出相乘后的预测矩阵，即我们所要的评分矩阵
    '''
    def predict(self, user, item):
        predict = np.mat(user) * np.mat(item.T)
        return predict

    #主函数
    def main(self):
        #获取U-I的{1:{2,5,1,2}....}数据
        user_ratings_train = self.load_data(self.train_data_path)
        #获取测试集的评分矩阵
        self.load_test_data(self.test_data_path)
        #将test_data矩阵拍平
        for u in range(self.user_count):
            for item in range(self.item_count):
                if int(self.test_data[u][item]) == 1:
                    self.test[u * self.item_count + item] = 1
                else:
                    self.test[u * self.item_count + item] = 0
        #训练
        for i in range(self.train_count):
            print(f'--------共{self.train_count}轮训练，目前正在进行第{i + 1}轮测试--------')
            self.train(user_ratings_train)  #训练10000次完成
        predict_matrix = self.predict(self.U, self.V) #将训练完成的矩阵內积

        # 输出给用户0推荐的5部电影
        predict_matrix_np = predict_matrix.getA()
        sort_0 = np.argsort(-predict_matrix_np[0])
        print('给用户0推荐的5部电影编号为：')
        for i in range(5):
            print(sort_0[i])

        # 预测
        self.predict_ = predict_matrix.getA().reshape(-1)  #.getA()将自身矩阵变量转化为ndarray类型的变量
        print("predict_new", self.predict_)
        self.predict_ = pre_handel(user_ratings_train, self.predict_, self.item_count)
        auc_score = roc_auc_score(self.test, self.predict_)
        print('AUC:', auc_score)
        # Top-K evaluation
        scores.topK_scores(self.test, self.predict_, 5, self.user_count, self.item_count)
    '''
    函数说明：对结果进行修正，即用户已经产生交互的用户项目进行剔除，只保留没有产生用户项目的交互的数据
    Paramaters:
        输入用户项目字典集，以及一维的预测矩阵，项目个数
    Returns:
        输出修正后的预测评分一维的预测矩阵
    '''
def pre_handel(set, predict, item_count):
    # Ensure the recommendation cannot be positive items in the training set.
    for u in set.keys():
        for j in set[u]:
            predict[(u - 1) * item_count + j - 1] = 0
    return predict

if __name__ == '__main__':
    #调用类的主函数
    bpr = BPR()
    bpr.main()

计算模型指标的代码：scores.py（与BPR_basical.py文件放在同一个子目录下）：

# -*- coding: utf-8 -*-
"""scores.ipynb

Automatically generated by Colaboratory.

Original file is located at
    https://colab.research.google.com/drive/17qoo1U4Iw58GRDDIyCaB2GmbRUg1gTPd
"""

import heapq
import numpy as np
import math
#计算项目top_K分数
def topK_scores(test, predict, topk, user_count, item_count):

    PrecisionSum = np.zeros(topk+1)
    RecallSum = np.zeros(topk+1)
    F1Sum = np.zeros(topk+1)
    NDCGSum = np.zeros(topk+1)
    OneCallSum = np.zeros(topk+1)
    DCGbest = np.zeros(topk+1)
    MRRSum = 0
    MAPSum = 0
    total_test_data_count = 0
    for k in range(1, topk+1):
        DCGbest[k] = DCGbest[k - 1]
        DCGbest[k] += 1.0 / math.log(k + 1)
    for i in range(user_count):
        user_test = []
        user_predict = []
        test_data_size = 0
        for j in range(item_count):
            if test[i * item_count + j] == 1.0:
                test_data_size += 1
            user_test.append(test[i * item_count + j])
            user_predict.append(predict[i * item_count + j])
        if test_data_size == 0:
            continue
        else:
            total_test_data_count += 1
        predict_max_num_index_list = map(user_predict.index, heapq.nlargest(topk, user_predict))
        predict_max_num_index_list = list(predict_max_num_index_list)
        hit_sum = 0
        DCG = np.zeros(topk + 1)
        DCGbest2 = np.zeros(topk + 1)
        for k in range(1, topk + 1):
            DCG[k] = DCG[k - 1]
            item_id = predict_max_num_index_list[k - 1]
            if user_test[item_id] == 1:
                hit_sum += 1
                DCG[k] += 1 / math.log(k + 1)
            # precision, recall, F1, 1-call
            prec = float(hit_sum / k)
            rec = float(hit_sum / test_data_size)
            f1 = 0.0
            if prec + rec > 0:
                f1 = 2 * prec * rec / (prec + rec)
            PrecisionSum[k] += float(prec)
            RecallSum[k] += float(rec)
            F1Sum[k] += float(f1)
            if test_data_size >= k:
                DCGbest2[k] = DCGbest[k]
            else:
                DCGbest2[k] = DCGbest2[k-1]
            NDCGSum[k] += DCG[k] / DCGbest2[k]
            if hit_sum > 0:
                OneCallSum[k] += 1
            else:
                OneCallSum[k] += 0
        # MRR
        p = 1
        for mrr_iter in predict_max_num_index_list:
            if user_test[mrr_iter] == 1:
                break
            p += 1
        MRRSum += 1 / float(p)
        # MAP
        p = 1
        AP = 0.0
        hit_before = 0
        for mrr_iter in predict_max_num_index_list:
            if user_test[mrr_iter] == 1:
                AP += 1 / float(p) * (hit_before + 1)
                hit_before += 1
            p += 1
        MAPSum += AP / test_data_size
    print('MAP:', MAPSum / total_test_data_count)
    print('MRR:', MRRSum / total_test_data_count)
    print('Prec@5:', PrecisionSum[4] / total_test_data_count)
    print('Rec@5:', RecallSum[4] / total_test_data_count)
    print('F1@5:', F1Sum[4] / total_test_data_count)
    print('NDCG@5:', NDCGSum[4] / total_test_data_count)
    print('1-call@5:', OneCallSum[4] / total_test_data_count)
    return

数据集也都与上面两个文件放在同一个文件夹下，数据集地址：

链接: https://pan.baidu.com/s/1pB0YDG6zhLT33FKn1n3bUA 提取码: csym

配置好环境后直接运行BPR_basical.py文件即可。

结果展示：

4. 参考资料

1. 贝叶斯个性化排序(BPR)算法小结

2. 用tensorflow学习贝叶斯个性化排序(BPR)

3. 推荐系统中的排序学习

4. BPR 贝叶斯个性化排序

5. BPR贝叶斯个性化推荐算法—推荐系统基础算法（含python代码实现以及详细例子讲解）

6. 推荐算法之贝叶斯个性化排序 BPR

7. 原论文