tf2.0先试试图片（七）——CNN卷积神经网络

之前已经介绍了TenforFlow的基本操作和神经网络，主要是全联接网络的一些概念：

7.0 简介

我们首先思考一下什么叫深度学习。深度学习的深度，一般是指神经网络的层数，可是到目前为止，我们介绍的全连接网络，组多也只有5层，并不能称得上是“深度学习”。那么深度学习和神经网络到底是什么关系呢？
1980年代，基于多层感知机实现的网络模型行就叫神经网络。但是由于当时计算能力、数据量等因素的限制，当时的神经网络往往都曾数不多，也叫浅层神经网络，这种神经网络提取数据高层特征的能力一般，表达能力有限。虽然在手写数字识别等简单任务上也取得了不错的效果，但很快就被支持向量机等模型超越。
但对于神经网络的研究却始终没有中断，直到后来网络层数越来越多，为区别于原来的浅层神经网络，这些神经网络叫做深度神经网络，深度学习的名称也因此流行。
本章要介绍的卷积神经网络深度可以到达上百层。

7.1 全连接网络的问题

我们首先分析全连接网络的问题，考虑一个输入是手写数字图片的4层神经网络，输入打平后是28*28，784维，中间三层都是256维，输出是10维。这样一个神经网络需要多少参数呢？
首先看第一层，784 * 256 * 256 = 200960。同样的算法涮出后边3层的参数量为65792，65792，2570，总参数约为34万个，约占内存1.3M。而实际上网络在训练的时候，还要保存计算图，梯度信息，输入值，中间结果等信息，占用资源会比这多很多。
在计算资源有限的年代，全连接网络较高的内存占用，严重限制了神经网络向大规模、深层次发展。

7.1.1 局部相关性

接下来我们就探讨如何避免**全连接网络的参数量过大问题。**假设有一个单通道的2D图片，当使用全连接网络是，首先要将图片打平成1D向量，再将每个像素点与每个输出点两两相连。

可以看到图片的输入节点都要与输出节点两两相连，这种稠密的连接方式需要大量的参数，且计算量很大。
$$o_j=\sigma \left(\sum _{i\in node(I)}{w}_{i,j}{x}_i+b_i\right)$$
其中$o_j$表示输出层的第j个元素，node(I)表示输入层的所有节点。
既然这种每个输出节点都和所有输入节点相连的方式会消耗大量资源，那么可不可以换种方式呢，输出节点只跟部分重要的节点相连。我们可以分析输入节点跟输出节点的重要性分布。
$$o_j=\sigma \left(\sum _{i\in top(I,j,k)}{w}_{i,j}{x}_i+b_i\right)$$
其中top(I, j, k)表示所有输入节点I中跟跟输出节点j最相关的k个节点。通过这种方式可以将全连接中||I|| * ||J||个权值参数减少到k * ||J||个，其中||I||, ||J||分别代表I层的节点数、J层的节点数。
于是问题就变成了如何从所有I个节点中找到和输出节点j最重要的k个节点。这本身是个非常难的问题。但我们可以利用先验知识将其进一步简化。
我们认为每个像素点跟他周围的像素点的关联度更大。那么我们就可以将重要性分布简化为，只考虑像素点周围距离小于$\frac{k}{\sqrt{2}}$的像素点，网格之外的像素点不考虑，这个网格窗口也叫做感受野。

利用局部相关性，我们把感受野的窗口高、宽记为k后，输入输出关系如下：
$$o_j=\sigma \left(\sum _{dist(i,j)<=\frac{k}{\sqrt{2}}}{w}_{i,j}\cdot x_i+b_i\right)$$

7.1.2 权值共享

引入局部相关性后，已经将每层的参数量从||I|| * ||J|| 减少到k * k * ||J||个，k一般是个较小的值（1，3，5），因此参数量减少了很多。
能否将参数量进一步减少呢，答案是肯定的。通过权值共享的思想，对于每个输出节点$o_j$，均使用相同的权值矩阵$W$，那么无论输出节点J的数量是多少，参数量都为k*k个。这种权值共享的局部链接层网络其实就是卷积神经网络。
接下来我们将从数学角度介绍卷积云算。

7.1.3 卷积运算

对于窗口k*k内的所有像素，采用权值相乘累加的方式提取特征，每个输出节点对应感受野区域内的信息。这种运算在信号处理领域，叫做离散卷集运算。
在信号处理领域，卷积运算被定义成两个函数的积分：函数$f(x)$、函数$g(\tau )$，其中$g(\tau )$经过翻转$g(-\tau )$和平移后变成$g(n-\tau )$。卷积的卷是指平移翻转操作，积是指积分。
$$(f\otimes g)(n)={\int }_{-\inf }^{\inf }f(\tau )g(n-\tau )d\tau$$
离散卷积将积分运算换成了累加运算:
$$(f\otimes g)(n)=\sum _{\tau =-\inf }^{\inf }f(\tau )g(n-\tau )$$
现在我们考虑2D的卷积运算：
$$[f\otimes g](m,n)=\sum _{i=-\inf }^{\inf }\sum _{j=-\inf }^{\inf }f(i,j)g(m-i,n-j)$$

首先将卷积函数翻转（x，y轴都翻转一次）得到$g(-i,-j)$。当(m, n) = (-1, -1)时，$g(-1-i,-1-j)$表示将卷积函数翻转一次后再向左，向上平移一个单元。

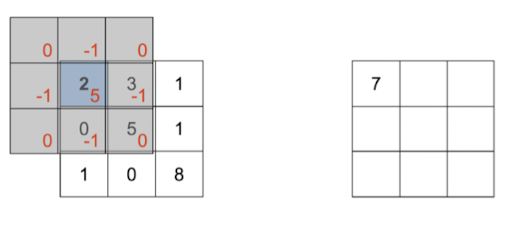
同样的方法(m, n) = (0,-1)时：

。。。
用这种方式计算出$m\in [-1,1],n\in [-1,1]$的所有值得到：

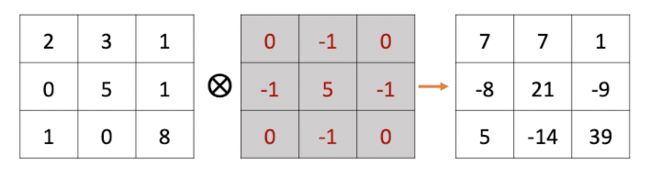
通过卷积运算之后，我们就得到一个新的特征图。
现在我们把公式记作：
$$[f\cdot g](m,n)=\sum _{i\in [-w/2,w/2]}\sum _{j\in [-h/2,h/2]}f(i,j)g(i-m,j-m)$$
通过对比标准的卷积函数发现，没有了反转操作。对于神经网络来说，目标是学到一个g(m, n)使得损失函数最小，至于g(m, n)是不是符合标准定义的卷积核并不重要。
可以看出，从数学角度，卷积就是完成了一次卷积运算，从权值共享和局部相关的角度，也是殊途同归。

7.2 卷积神经网络

卷积神经网络通过充分利用局部相关性和权值共享的思想，大大减少了网络的参数量，从而提高了训练效率，更容易实现大规模的深度网络。

7.2.1 单通道输入和单卷积核

单通道是指输入是有一个通道，例如灰度图。如下所示，输入为(1 * 5 * 5)的图片。卷积和是(1 * 3 * 3)。
卷积核首先和对应的感受野，对应元素相乘再求和得到一个值，卷集后输出的第一个元素。
然后卷集合不断向右滑动制定步长，得到输出的第二个值。
直到卷集合滑动到最右下端。

由于输入是单通道，只有一个卷积核，因此输出也只有一个通道。

7.2.2 多通道输入和单卷积核

多通道，是指输入不止一个通道，例如RGB图片会有3个通道。
如下图所示，输入是(3 * 5 * 5)的图片。卷积核是(3 * 3 * 3)的，多通道的单卷积核数量要跟输入数据的通道数量相等。

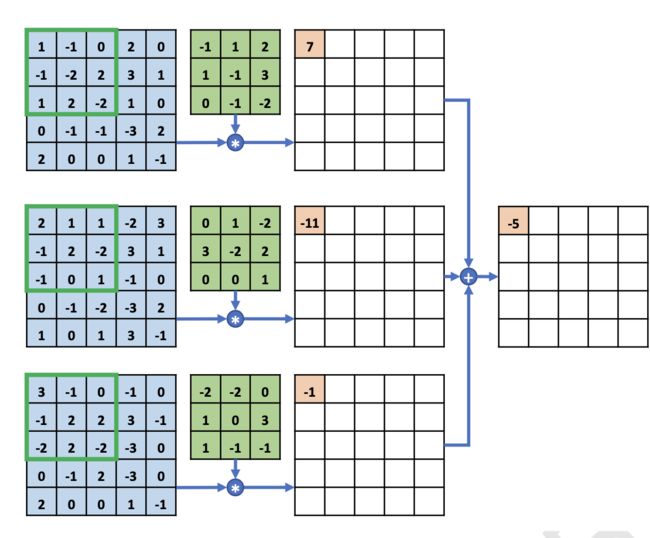
卷集合和对应的感受野对应元素相乘求和，再将不同通道的结果相加，就是输出的第一个元素。由于卷积核是单核的，一次输出也只有一个通道。

7.2.3 多通道输入和多卷积核

这是最常见的卷积结构。输入为(3 * 5 * 5)，卷积核为(n * 3 * 5 * 5)

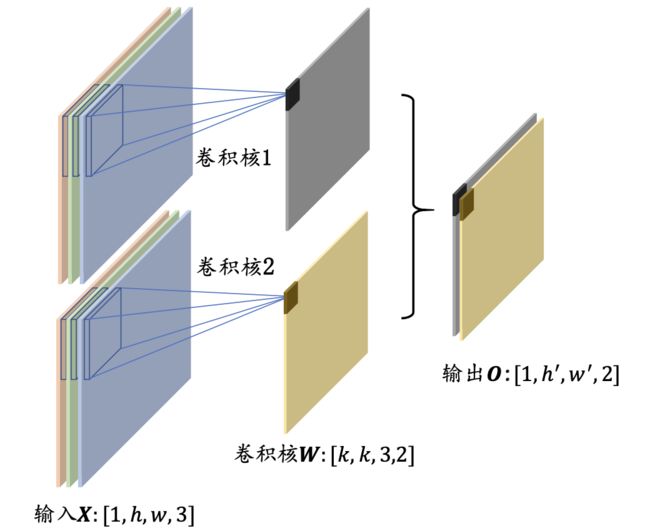
每个卷集合执行多通道输入和单卷积核的操作，然后得到不同的输出，最终形成输出的n个通道。输出的通道数量跟卷积核的数量一致。

7.2.4 步长

步长是指卷积核每次移动的长度，也就是感受野窗口每次变化的长度。为什么要设置不同的步长呢， 因为有些图片信息的密度较大，需要更大的感受野密度，防止信息遗漏。而有些图片信息密度小，需要比较小的感受野密度就可以。而控制感受野密度，就需要通过步长了。

合理控制不长，能够在不牺牲准确率的前提下，减少计算代价。

7.2.5 填充

我们前边讲过的卷集，仔细观察会发现每次卷集之后，输出的长、宽都会变小。随着卷集层的增加，每个通道会变的特别小，如何避免每次卷集之后的维度变小呢？答案就是填充。再卷集之前，现将该通道的长、款分别在四周填充0，使该通道的长、宽变大，卷集之后就能维持原来的大小了。

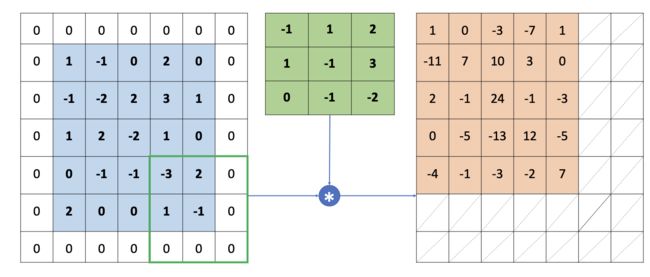
那么如何判断卷积后，新的输出的长、宽呢？假设输入尺寸为$[b,h,w,c_{out}]$，生产出尺寸$[b,h^{{}^{\prime }},w^{{}^{\prime }},c_{out}]$，其中$p_h$为对输入的h方向的填充数量，他们有如下数学关系：
$$h^{{}^{\prime }}=\lfloor \frac{h+2\ast p_h-k}{s}\rfloor +1$$

7.3 卷基层实现

在TensorFlow中，既可以通过自定义权值的方式，底层实现卷积网络，也可以通过Keras提供的高层借口轻松实现卷基层类。

7.3.1 自定义权值

x = tf.random.normal([2, 5, 5, 3])
w = tf.random.normal([3, 3, 3, 4])
out = tf.nn.conv2d(x, w, strides=1, padding=[[0, 0], [0, 0], [0, 0], [0, 0]])
out.shape

TensorShape([2, 3, 3, 4])

上述卷积中，输入x维度为[2, 5, 5, 3]，其中第一维是batch_size，第二、三维是图片每个通道的长、高，第四维是图片的通道数。卷积核w，第一维是输入的维度，第二、三维是卷积核的长、高，第四维是卷积核数，也是输出的通道数。
conv2d的padding参数，[[0, 0], [上, 下], [左, 右], [0, 0]]，现在我们尝试改变padding：

 x = tf.random.normal([2, 5, 5, 3])
w = tf.random.normal([3, 3, 3, 4])

out = tf.nn.conv2d(x, w, strides=1, padding=[[0, 0], [1, 1], [1, 1], [0, 0]])
out.shape
TensorShape([2, 5, 5, 4])

输出高维5，刚好符合前节中卷积后的h公式。
padding除了手动设置外，还可以直接设置成’SAME’，能保证结果的长、高跟输入保持一致。

7.3.2 卷积层类

Keras搞成借口中，提供了tf.keras.layers.Conv2D()类，可以很方便的实现卷积过程。跟tf.nn.conv2d()计算函数不同，ConvD()类自动定义卷积核W和偏置b。
卷积层类，只需要指定卷积核数量filters，卷积核大小kernel_size，步长strides，填充padding即可。

x = tf.random.normal([2, 5, 5, 3])
conv2d = tf.keras.layers.Conv2D(4, kernel_size=3, strides=1, padding='SAME')
out = conv2d(x)
out.shape

TensorShape([2, 5, 5, 4])

conv2d.trainable_variables

用conv2d.trainable_variables可返回该卷积层卷积核的参数W和b。也可以用conv2d.kernel和conv2d.bias分别访问W和b。

7.4 LeNet-5 实战

LeNet-5是第一个被商用的卷积神经网络，曾经广泛应用在有这边吗、支票号识别的人数中。他接受32*32的字符图片。

import tensorflow as tf 
from tensorflow.keras.datasets import mnist

model = tf.keras.Sequential([
tf.keras.layers.Conv2D(6, kernel_size=3, strides=1),
tf.keras.layers.MaxPooling2D(pool_size=2, strides=2),
tf.keras.layers.ReLU(),
tf.keras.layers.Conv2D(16, kernel_size=3, strides=1),
tf.keras.layers.MaxPooling2D(pool_size=2, strides=2),
tf.keras.layers.ReLU(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(120, activation='relu'),
tf.keras.layers.Dense(84, activation='relu'),
tf.keras.layers.Dense(10)
])

model.build(input_shape=[None, 28, 28, 1])
model.summary()

(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = tf.expand_dims(X_train, axis=3)
X_test = tf.expand_dims(X_test, axis=3)
y_train= tf.one_hot(y_train, depth=10)

criteion = tf.keras.losses.CategoricalCrossentropy(from_logits=True)
model.compile(
    optimizer='adam', loss=criteion , metrics=['accuracy']
)

model.fit(X_train, y_train, batch_size=64, epochs=1, shuffle=True)

也可以用如下方式进行训练:

train_ds = tf.data.Dataset.from_tensor_slices((X_train, y_train)).batch(64)
test_ds = tf.data.Dataset.from_tensor_slices((X_test, y_test)).batch(64)
adam = tf.keras.optimizers.Adam()

for epoch in range(2):
    for step, (x, y) in enumerate(train_ds):
        with tf.GradientTape() as tape:
            out = model(x)
            loss = criteion(y, out)
        grads = tape.gradient(loss, model.trainable_variables)
        adam.apply_gradients(zip(grads, model.trainable_variables))
        if step % 100 ==  0:
          print('------------------------', epoch, step, float(loss))

7.5 表示学习

研究人员发现，网络层数越深，模型的表达能力越强，也就越有可能获得更好的结果。那么层层堆叠的卷积网络到底学到了什么特征，使得层数越深，表达能力越强呢？
我们通过将特征图利用反卷积网络映射回原始图片，即可查看该层特征图学到了什么特征。
图片数据的识别过程，一般也可以认为是表示学习的过程。从接受到原始像素开始，逐渐提取边缘、角点等底层特征，再到纹理等中层特征，再到头部、物体部件等高层特征，最后的网络层基于这些学习到的抽象特征表示做分类逻辑的学习。
从表示学习的角度理解，卷积神经网络层层堆叠的提取特征，网络训练过程也就是特征学习的过程，最后基于学习到的高层抽象特征可以很容易的进行分类任务。
应用表示学习的思想，一个好的卷积神经网络，往往有更好的特征提取能力，而这种特征的提取方法一般是通用的。例如，在猫狗任务上学到的头、脚等特征的抽象能力，同样可以迁移到其他任务上，并且有比较好的效果。基于这个思想，在A任务上训练的神经网络，可以将其前几层迁移到B任务上，因为不同任务的底层特往往相差不大。这种方式是迁移学习的一种。

7.6 梯度传播

神经网络中，卷积层是通过移动感受野的方式实现离散卷积的，那么它的梯度是怎样进行传播的呢？
我们以33单通道图片和22单卷积核为例，说明一下卷积的梯度。

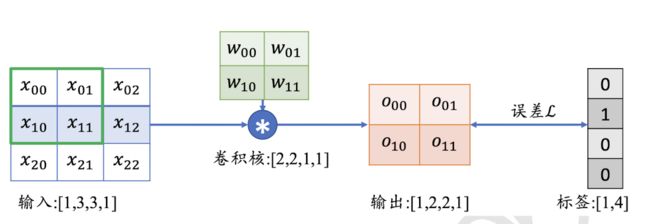
假设卷积输出，直接打平与表现计算误差。
我们要计算出W的梯度，并更新W。
$$\frac{\partial L}{\partial w_{00}}=\sum _{i\in (00,01,10,11)}\frac{\partial L}{\partial o_i}\frac{\partial o_i}{\partial w_{00}}$$
其中$\frac{\partial L}{\partial o_i}$可以通过损失函数很容易计算出来，我们直接考虑$\frac{\partial o_i}{\partial w_{00}}$:
$$\frac{\partial o_{00}}{\partial w_{00}}=\frac{\partial (x_{00}\ast w_{00}+x_{01}\ast w_{01}+x_{10}\ast w_{10}+x_{11}{w}_{11})}{\partial w_{00}}=x_{00}$$
其他梯度计算方式相同。
由此可见，移动感受野的方式，也是可以计算出梯度的。只不过当网络层变得巨大时，梯度的推导将会变得十分繁琐。不过深度学习框架可以帮我们很好的完成那些工作 。

7.7 池化层

在卷积层中，可以通过调节步长来调节特征图的高宽，从而降低网络参数量。还有一种有效的方式实现尺寸缩减，它就是池化层。
通过对局部相关的一组元素进行采样或聚合，形成一个新的元素。例如最大池化，就是从局部相关的一组元素中选出最大的一个，平均池化就是从中算出平均值。

如上图所示，最大池化就是在局部相关的一组数据中，找出最大的元素作为输出，输出到新的特征图里。
由于池化没有要学习的参数，计算简单，并且可以有效降低特征图的尺寸，在计算机视觉中有广泛的应用。
通过精心计算池化层的感受野（高宽）和步长，可以实现有效降维。例如k=2，s=2时，输出的高宽只有输入高宽的一半。

7.8 BatchNorm层

虽然卷积网络可以使神经网络参数大大减少，从而使更深层次的网络结构可以实现。但在残差网络出现之前，网络的加深会出现网络变得非常不稳定，网络长时间不更新、不收敛，网络对超参数比较敏感，甚至微量扰动也会网络训练轨迹变得完全不一样。
Batch Normalization（BatchNorm或BN）层的引入，使得网络的超参数设定可以更加灵活，譬如更大的学习率、更随意的初始化参数，同时网络的收敛速度更快，性能也更好。通过堆叠Conv-BN-ReLU-Pooling的方式，往往可以获得不错的模型性能。
我们将BN层的输入、输出分别用$x$ 和 $\tilde{x}$ 表示。再分别从训练阶段和测试阶段的角度分析BN层。

首先看训练阶段：
$${\tilde{x}}_{train}=\frac{x_{train}-{\mu }_B}{\sqrt{{\sigma }_B^2+\epsilon }}\cdot \gamma +\beta$$
BN层的输出公式如上所示。同时按照
$$\begin{gathered} {\mu }_r=momentum\cdot {\mu }_r+(1-momentum)\cdot {\mu }_B \\ {\sigma }_r^2=momentum\cdot {\sigma }_r^2+(1-momentum)\cdot {\sigma }_B^2 \end{gathered}$$
的方式更新${\mu }_r$ 和 ${\sigma }_r^2$ 。其中momentum是个超参数，当其为0时，表示直接用最新的Batch的均值、方差；当其为1表示其保持不变。

在看测试阶段：
$${\tilde{x}}_{test}=\frac{x_{test}-{\mu }_r}{\sqrt{{\sigma }_r^2+\epsilon }}\cdot \gamma +\beta$$
在测试阶段计算BN时，${\mu }_r,{\sigma }_r,\gamma ,\beta$ 均来自测试阶段统计或优化的结果，测试阶段本身不会对其更新。

7.8.2 反向更新

在训练阶段的反向更新中，反向传播算法根据损失函数$L$ 求出$\frac{\partial L}{\partial \gamma }$ 和 $\frac{\partial L}{\partial \beta }$ ，在通过梯度更新法则更新$\gamma$ 和 $\beta$。

需要注意的是，对于2D图片X: [b, w, h, c]来说，并不会计算每个点的${\mu }_r$和${\sigma }_r$，而是在通道轴c上面，统计所有点的${\mu }_r$和${\sigma }_r$。也就是说，有多少个通道，就有多少个${\mu }_r$和${\sigma }_r$。

x = tf.random.uniform([100, 32, 32, 3])
x = tf.respahe(x, (-1, 3))
x.shape # 102400, 3
ub = tf.reduce_mean(x, axis=0)
ub.shape # 3

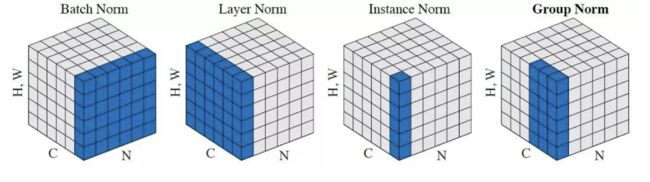
不同的Normalization的统计维度有所不同。

• Layer Norm: 统计每个样本所有维度上的均值、方差
• Instance Norm: 统计每个样本，在每个通道上的均值、方差
• Group Norm: 将通道C分成若干组，统计每个样本在通道组内的均值、方差。

7.8.3 BN层实现

在TensorFlow中，可以通过layers.BatchNormalization()很方便的实现BN层。由于BN层在训练阶段和测试阶段的行为不同，因此需要通过设置training标志来区分训练模式和测试模式。

import tensorflow as tf 

netword = tf.keara.Sequences([
  tf.keras.layers.Conv2D(6, kernel_size=3, strides=1),
  tf.keras.layers.BatchNormalization(),
  tf.keras.layers.MaxPooling2D(pool_size=2, strides=2),
  tf.keras.layers.ReLU(),
  tf.keras.layers.Conv2D(16, kernel_size=3, strides=1),
  tf.keras.layers.BatchNormalization(),
  tf.keras.layers.MaxPooling2D(pool_size=2, strides=2),
  tf.keras.layers.Relu(),
  tf.keras.Flatten(),
  tf.keras.layers.Dense(128, activation='relu'),
  tf.keras.layers.Dense(84, activation='relu'),
 	tf.keras.layers.Dense(10)
])

# 训练阶段，需要将training设为True
with tf.GraidentTape() as tape:
  x = tf.expand_dim(x, axis=3)
  out = network(x, training=True)
  
 # 测试阶段，要将training设为False
out = network(x_test, training=False)
  
 

7.9 经典卷积网络

本节将会介绍一些经典的卷积神经网络。自2012年AlexNet被提出来之后，各种卷积神经网络也相继被提出来了，其中比较有代表性的有VGG系列，GoogleNet系列，ResNet系列，DenseNet系列，他们的网络层数整体呈逐渐增多的趋势。而且在ImageNet等数据集上的表现十分抢眼，ResNet首次将神经网络层数提升到了152层，错误率也降低到3.57%，超越了人来表现。

7.9.1 AlexNet

2012年，AlexNet在ImageNet数据集分类任务上获得了冠军。首次提出了8层的神经网络模型行AlexNet。他的输入为224*224的RGB彩色图片数据，经过5个卷积层和3个全简介层后，最终得到该样本属于1000的分了的概率。为了降低特征图的维度，AlexNet在第1，2，5层之后加入了MaxPooling层。

AlexNet的创新之处：

• 神经网络达到8层。
• 采用了ReLU激活函数（之前的神经网络大多采用sigmoid激活函数，容易出现梯度消失问题）。
• 引入Dropout层，提高模型泛化能力，减少过拟合。

7.9.2 VGG系列

AlexNet在ImageNet上的优越性能，使业界朝着更深层的网络模型方向研究。2014年VGG系列问世，包括VGG11，VGG13，VGG16，VGG19等。以VGG16为例，他的输入是224 * 224 * 3的图片，再经过2个Conv-Conv-Pooling层和3个Conv-Conv-Conv-Pooling层，最后通过3个全连接层得到图片属于1000个分类的概率。（16 = 2 * 2 + 3 * 3 + 3）。

VGG系列网络的创新之处在于：

• 网络深度有所增加，最多到19层。
• 全部采用了更小的卷积核（3 * 3），相较于AlexNet中7 * 7的卷积核，参数更少，计算代价更低。
• 采用更小的池化层2 * 2，strides=2，AlexNet中采用的是3 * 3，strides=2。

7.9.3 GoogleNet

3 * 3的卷积核参数更少，计算量更低，性能更优越。因此业界开始探索最小的卷积情况：1 * 1卷积。

[图片上传失败…(image-a1c916-1628692499958)]

例如上图所示，输入是5 * 5的3通道图片，于单个1 * 1卷积核进行运算（单个卷积核通道数与输入一致），得到新的特征图。输出的特征图的通道数，也就是卷积核的核数。1 * 1卷积的特别之处在于它不改变特征图的高宽（维度），只改变特征图的通道数。

2014年ImageNet图片分类的冠军方案GooleNet，就大量使用了3 * 3和1 * 1卷积，网络层数达到了22层。虽然GoolgNet的层数远远大于AlexNet，但模型参数只有AlexNet的$\frac{1}{12}$，同时性能也远远好于AlexNet。

GoogleNet网络采用了模块化的设计思想。设计出Inception模块，然后大量堆叠Inception模块，最终形成了复杂的网络结构。

[图片上传失败…(image-8934b0-1628692499958)]

Inception：

• 1 * 1卷积
• 1 * 1卷积，后接3 * 3卷积
• 1 * 1卷积后接5 * 5卷积
• 3 * 3最大池化后接1 * 1卷积

7.10 卷积层的变种

卷积神经网络的研究，不仅产生了各种优秀的神经网络模型，还提出了一些卷积层的变种。

7.10.1 空洞卷积

普通卷积中，人们为了减少参数量，往往将卷积核设置的很小，如1 * 1，3 * 3。但很小的卷积核同样会导致感受野很小，而增大感受野就要增加卷积核数，导致参数量变大。因此需要权衡。

空洞卷积的提出，能够很好的解决这个问题。空洞卷积是在普通卷积的基础上加了一个Dilation Rate的参数，用于控制感受野区域的采样步长。如下图所示，当感受野的Dilation Rate为2时，感受野内每个采样点的间隔为2，即每两个点采样出一个点。当Dilation Rate为1时，空洞卷积退化为普通卷积。

这样虽然感受野所有增加，但参与计算的卷积核数却没有增加。实现了增大感受野，没增加卷积核。但使用空洞卷积设计神经网络时，要避免出现网格效应，同时较大的Dilation Rate不利于小物体的检验和语义分割等任务。

在TensorFlow中可以使用tf.keras.layers.Conv2D()，并添加dilation_rate参数来选择使用普通卷积还是空洞卷积。

x = tf.random.normal((1, 7, 7, 1))
layer = tf.keras.layers.Conv2D(1, kernel_size=3, dilation_rate=2)

当dilation_rate为1时，使用普通卷积进行运算；当其大于1时，使用空洞卷积进行运算。

7.10.2 转制卷积

转置卷积，也有部分资料叫反卷积。但实际上反卷积在数学上时卷积过程的逆过程，但转置卷积并不能恢复出原始的卷积输入，因此反卷积的称呼并不准确。转置卷积就是通过将输入的元素之间填充大量的padding，从而实现输出的维度大于输入的维度，来实现上采样的目的。

o + 2p - k为s的倍数时

考虑输入为2 * 2的单通道特征图，转置卷积核为3 * 3，步长为2，填充p=0。首先在数据点中间均匀插入s - 1个数据点，得到3 * 3的矩阵。根据填充量在矩阵周围填充相应k - p - 1 = 3 - 0 - 1行/列，此时输入特征图的高宽为7 * 7。然后在7 * 7的张量上进行3 * 3的卷积核，$s_{{}^{\prime }}$ = 1，填充padding=0的卷积运算，即得到输出为5 * 5的特征图。

我们直接给出转置卷积输入与输出的维度关系，当o + 2p - k为s的倍数时：
$$o=(i-1)\ast s+k-2p$$
转置卷积并不是普通卷积的逆过程，但二者之间有一定联系，同时转置卷积也是基于普通卷积计算来的。输入x再经过普通卷积后得到输出o = Conv(x)，将o送入转置卷积后得到$x_{{}^{\prime }}$，其中$x_{{}^{\prime }}$不等于x，但$x_{{}^{\prime }}$的形状与x相同。

可用TensorFlow实现转置卷积运算

x = tf.range(25) + 1 
x = tf.reshape(x, [1, 5, 5, 1])
x = tf.cast(x, tf.float32)

w = tf.constant([[-1, 2, -3.], [4, -5, 6], [-7, 8, -9]])
w = tf.expand_dims(w, axis=2)
w = tf.expand_dims(w, axis=3)

out = tf.nn.conv2d(x, w, strides=2, padding='VALID')

xx = tf.nn.conv2d_transpose(out, w, strides=2, padding='VALID', output_shape=[1, 5, 5, 1])

o + 2p - k 不为s的倍数

首先考虑卷积运算输出维度的表达式：
$$o=\lfloor \frac{i+2p-k}{s}\rfloor +1$$
当步长s>1是，由于向下取整，会出现不同输入维度i对应相同的输出o的情况。所以从转置卷积的角度讲，相同的输入i可能会对应不同的输出o。因此需要填充a行、a列来实现不同大小的输出，从而恢复普通卷积不同大小的输入的情况。其中a为：
$$a=(o+2p-k)\%s$$
次数转置卷积的输出变为：
$$o=(i-1)s+k-2p+a$$
在Tensorflow中不需要手动指定a，只需要制定输出尺寸即可。

矩阵角度

转置卷积的转置，是指卷积核矩阵W产生的稀疏矩阵$W^{{}^{\prime }}$，再经过转置后得到$W^{{}^{\prime }T}$之后，在进行矩阵相乘运算。普通的Conv2D并没有将$W^{{}^{\prime }}$转换成$W^{{}^{\prime }T}$的步骤。这也是转置卷积名称的由来。

考虑普通的卷积Conv2D运算：X和W，需要卷积核根据strides在行、列方向上循环获取感受野，并将每个窗口计算相乘累加，计算效率极低。为了加速运算，在数学上可以将卷积核W根据strides重排成稀疏矩阵$W^{{}^{\prime }}$，再通过$W^{{}^{\prime }}@X^{{}^{\prime }}$进行计算。

以4行4列的输入X，高宽为 3 * 3的卷积核，步长为1，无padding的卷积核W的卷积运算为例。

首先将输入打平，获得$X^{{}^{\prime }}$：

再将卷积核W根据strides转换成稀疏矩阵$W^{{}^{\prime }}$：

此时计算$W^{{}^{\prime }}@X^{{}^{\prime }}$得到$O^{{}^{\prime }}$，再转换成O。

如果给定O，希望得到与X大小相同的输出，该如何计算呢？

只需要将$W^{{}^{\prime }}$做转置即可。
$$X^{{}^{\prime }}=W^{{}^{\prime }T}@O^{{}^{\prime }}$$
转置卷积具有放大特征图的工程，在生成对抗网络，语义分割中有广泛应用。

7.10.3 分离卷积

这里以深度可分离卷积为例（Depth-wise Separable Convolution）为例。普通卷积在对多个通道数据进行计算时，卷积核的每个通道与输入的每个通道分别进行卷积运算，得到多通道的特征图，再对应元素相加产生单个卷积核的最终输出。

分离卷积的计算流程则不同，卷积核的每个通道与输入的每个通道进行卷积运算，得到多个通道的中间特征。这多个通道的中间特征分别进行1 * 1的卷积运算，得到多个高宽不变的输出，这些输出在通道轴上进行拼接，从而产生最终的分离卷积层的输出。

分离卷积的优势可以明显减少参数量。

7.11深度残差网络

AlexNet, VGG, GoogLeNet等网络模型的出现，将神经网络的发展带入了几十层的阶段。但当模型加深后，网络变得越来越难以训练，这主要是由于梯度消失和梯度爆炸现象造成的。当神经网络层数较多时，梯度信息从末层传输到首层，会出现梯度接近0或者变得非常大的情况。
那么该怎么解决梯度消失和梯度爆炸的问题呢，一个很容易想到的办法是，既然深层网络容易出现梯度消失和梯度爆炸问题，浅层网络往往能避开这个问题，那么可以尝试将深层网络回退成浅层网络。
通过在输入和输出之间添加一条直接链接的skip connection可以让神经网络具有回退的能力。以VGG13为例，假设在训练过程中出现了梯度消失问题，而10层的网络模型没有出现梯度消失问题，那么可以考虑在最后两个网络层添加skip connection。

7.11.1 ResNet原理

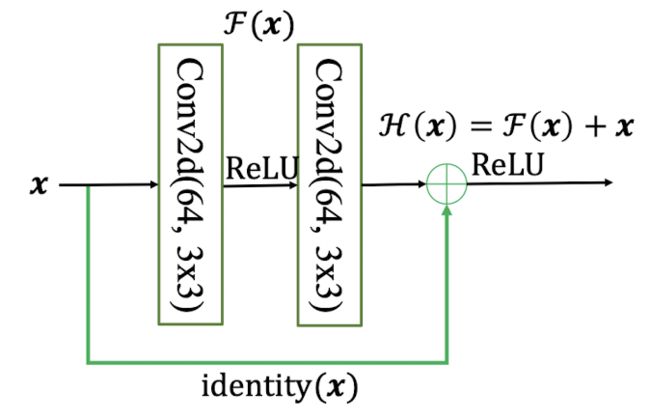
ResNet就是通过在输入和输出之间添加skip connection，从而实现层数的回退机制。输入x经过两个卷积层变成输出F(x)，在于输入x进行对应元素相加操作，得到最终输出。
$$H(x)=x+F(x)$$
H(x)叫做残差模块(ResBlock)。
为了保证输入x与卷积输出能够进行相加操作。x要与F(x)的shape保持一致。当shape不一致时，一般通过在skip connection上添加额外的卷积操作是他们具有相同的shape。