【数据结构】基础：图的遍历实现（附C++源代码）

【数据结构】基础：图的遍历实现（附C++源代码）

摘要：将会在数据结构专题中开展关于图论的内容介绍，其中包括四部分，分别为图的概念与实现、图的遍历、图的最小生成树以及图的最短路径问题。本文将介绍图的遍历，分别为深度优先遍历和广度优先遍历，需要了解其实现实现与方法。

---

前言：图的实现方式

本文中图的实现方法为邻接矩阵法，以下是对其类的基本描述，若需查看更加具体的内容，可以参考博客图的概念与基本实现。其重点可以概括为：

• Direction：表示是否为有向图
• _vertexs：记录了对应检索下的顶点元素
• _vIndexMap：记录了检索与顶点的对应关系
• _matrix：表示邻接矩阵

具体代码如下：

template<class V, class W, bool Direction = false, W MAX_WEIGHT = INT_MAX>
    class Graph {
        typedef Graph<V, W, Direction, MAX_WEIGHT> Self;

        private:
        vector<V> _vertexs; // 顶点集合
        map<V, int> _vIndexMap; // 顶点检索
        vector<vector<W>> _matrix; // 邻接矩阵

        public:
        Graph() = default;
        Graph(const V* vertexs,size_t vertexSize) {
            _vertexs.reserve(vertexSize);
            for (size_t i = 0; i < vertexSize; i++) {
                _vertexs.push_back(vertexs[i]);
                _vIndexMap[vertexs[i]] = i;
            }

            // 格式化
            _matrix.resize(vertexSize);
            for (auto& e : _matrix) {
                e.resize(vertexSize, MAX_WEIGHT);
            }
            //for (size_t i = 0; i < _matrix.size(); i++) {
            //	_matrix[i][i] = 0;
            //}
        }

        size_t GetVertexIndex(const V& v) {
            auto ret = _vIndexMap.find(v);
            if (ret != _vIndexMap.end()) {
                return ret->second;
            }
            else {
                throw invalid_argument("不存在的顶点");
                return -1;
            }
        }

        void AddEdge(const V& src, const V& dest, const W& weight) {
            size_t srcIndex = GetVertexIndex(src);
            size_t destIndex = GetVertexIndex(dest);
            AddEdgeByIndex(srcIndex, destIndex, weight);
        }

        void AddEdgeByIndex(size_t srcIndex, size_t destIndex, const W& weight){
            _matrix[srcIndex][destIndex] = weight;
            if (Direction == false) {
                _matrix[destIndex][srcIndex] = weight;
            }
        }
    }；

一、广度优先遍历（BFS）

概述：BFS，其英文全称是Breadth First Search，广度优先搜索是一种分层查找的过程。由于需要使用到分层查找，将会借助队列来帮助遍历。而为了避免重复访问的状况，借助一个容器，来记录访问状况。

算法实现：

• 将起点入队列，设置其为已访问的标识
• 对于队列进行空判断，若不为空，访问队列头并出队列，设置已访问标识。再通过邻接矩阵访问其邻接节点，并入队列
• 重复该过程直至队列为空

由于是广度优先遍历，可以对其添加层与层之间的关系，在此通过levelSize和level实现，具体操作为在起点入队列后，对于levelSize设置为1，每次遍历了levelSize个节点后，对于levelSize进行更新为队列的元素个数，同时更新level。

代码如下：

void BFS(const V& src) {
    queue<int> q;
    vector<bool> visited(_vertexs.size(), false);

    int srcIndex = GetVertexIndex(src);
    q.push(srcIndex);
    visited[srcIndex] = true;
    int levelSize = 1;
    int level = 1;

    while (!q.empty()) {
        cout << "层高：" << levelSize << " 层数：" << level << endl;
        for (size_t i = 0; i < levelSize; i++) {
            int front = q.front();
            q.pop();
            cout << "[" <<front << "|" << _vertexs[front] << "] ";
            for (size_t j = 0; j < _vertexs.size(); j++) {
                if (visited[j] == false && _matrix[front][j] != MAX_WEIGHT 
                    && _matrix[front][j] != 0) {
                    q.push(j);
                    visited[j] = true;
                }
            }
        }
        cout << endl;
        levelSize = q.size();
        level++;
    }
}

测试用例：

void TestBFSGraph() {
	Graph<char, int, true> g("0123", 4);
	g.AddEdge('0', '1', 1);
	g.AddEdge('0', '3', 4);
	g.AddEdge('1', '3', 2);
	g.AddEdge('1', '2', 9);
	g.AddEdge('2', '3', 8);
	g.AddEdge('2', '1', 5);
	g.AddEdge('2', '0', 3);
	g.AddEdge('3', '2', 6);
	cout << endl;
	g.Print();

	cout << endl;
	g.BFS('3');
}

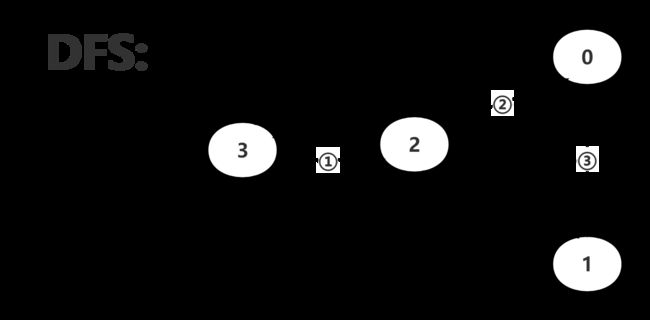
二、深度优先遍历（DFS）

概述：DFS 全称是 Depth First Search，中文名是深度优先搜索，是一种用于遍历或搜索树或图的算法。所谓深度优先，就是说每次都尝试向更深的节点走。该算法实现可以转换为子问题求解，即使用递归完成该遍历方式。

算法实现：

• 为了避免重复访问的情况，在此设定一个visited容器记录结点是否被访问。
• 算法的主题思路是使用递归完成，在递归访问一个结点后，通过邻接矩阵在此邻接点进行递归访问，直至访问完毕位置
• 同时在每次访问时需要对visited容器中是否访问进行修改为真。
• 为了防止出现多个森林的情况，在递归调用完起点后，进行对每个节点的再递归调用

代码如下：

void DFS(const V& src) {
    size_t srcIndex = GetVertexIndex(src);
    vector<bool> visited(_vertexs.size(), false);
    _DFS(srcIndex, visited);
    cout << "nullptr" << endl;

    // 但不是连通图的时候
    for (size_t i = 0; i < _vertexs.size(); i++) {
        if (visited[i] == false) {
            _DFS(i, visited);
            cout << " nullptr" << endl;
        }
    }
}
void _DFS(int srcIndex, vector<bool>& visited) {
    visited[srcIndex] = true;
    cout << "[" << srcIndex << "|" << _vertexs[srcIndex] << "] -> ";
    for (size_t i = 0; i < _vertexs.size(); i++) {
        if (_matrix[srcIndex][i] != MAX_WEIGHT && _matrix[srcIndex][i] != 0 && visited[i] == false) {
            _DFS(i, visited);
        }
    }
}

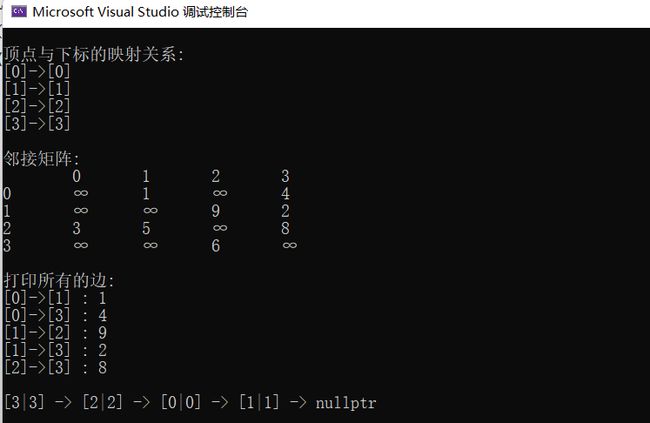
测试用例：

void TestDFSGraph() {
	Graph<char, int, true> g("0123", 4);
	g.AddEdge('0', '1', 1);
	g.AddEdge('0', '3', 4);
	g.AddEdge('1', '3', 2);
	g.AddEdge('1', '2', 9);
	g.AddEdge('2', '3', 8);
	g.AddEdge('2', '1', 5);
	g.AddEdge('2', '0', 3);
	g.AddEdge('3', '2', 6);
	cout << endl;
	g.Print();

	cout << endl;
	g.DFS('3');
}

---

补充：

1. 代码将会放到：C++/C/数据结构代码链接 ，欢迎查看！
2. 欢迎各位点赞、评论、收藏与关注，大家的支持是我更新的动力，我会继续不断地分享更多的知识！