The Category-theoretic Perspective of Statistical Learning for Amateurs

统计学习.范畴论视角

title: The Category-theoretic Perspective of Statistical Learning for Amateurs
author: Congwei Song
description: A representation in BIMSA

---

The Category-theoretical Perspective of Statistical Learning for Amateurs

Congwei Song

Email: [email protected]

Research Interest: Machine Learning, Wavelet Analysis

---

Abstract Statistical learning is a fascinating field that has long been the mainstream of machine learning/artificial intelligence. A large number of results have been produced which can be widely applied to real-world problems. It also leads to many research topics and also stimulates new research. This report summarizes some classic statistical learning models and well-known algorithms, especially for amateurs, and provides a category-theoretic perspective on understanding statistical learning models. The goal is to attract researchers from other fields, including basic mathematics, to participate in the research related to statistical learning.

Keywords Statistical Learning, Statistics, Category Theory, Variational Models, Neural Networks, Deep Learning

Abbreviations
distr.: distribution(s)
var.: variable(s)
cat.: category(ies)
rv: random varible(s)

Notations

• $P(X)$: distr. of target rv $X$
• $P(X|\theta )$: parameteric distr.

---

Introduction

• Probability theory/Statistics
• Category theory
• Statistical Learning
• Classiscal models of statistical Learning
• Advanced models
• Misc

---

Probability theory

Definition (Probability Model)
The probability model is a probability measure sp, denoted by $(\Omega ,\mathcal{A},P)$; or $(\mathcal{X},P(X))$, as its pushback by the rv $X$, where $\mathcal{X}$ is the sample space of $X$.

$X\sim P$: the distr. of $X$ is $P$, or draw $X$ from $P$

---

Statistics

Definition (Statistical Model)
The statistical model is a family/set of probability models denoted by $(\Omega ,\mathcal{A},\{P_{\lambda }\})$ (with common ambient space) or $(\mathcal{X},\{P_{\lambda }\})$ (with common sample space which is the range of a target rv $X$), denoted by $P(X)$ for short.

Parameterized version: $(\mathcal{X},\{P(X|\theta )\},\theta \in \Theta )$ where $\Theta$ is the parameter space, denoted by $P(X|\theta )$ for short.

Example
$N(\mu ,{\sigma }^2),Cat(p)$

---

Definition (Baysian Model)
THe Baysian model is a statistical model with priori distr. of parameters, as
$(M_{\theta },p(\theta ))$, where $M_{\theta }$ is a given statistical model.

Definition (Baysian Hierachical Model)
$(M_{\theta },p(\theta |\alpha ),p(\alpha ))$

---

Category theory of Statistical Models

• $\mathcal{P}rob$: cat. of all probability models,
• ${\mathcal{P}rob}_X$: sub-cat. of $\mathcal{P}rob$ with the form of $(\mathcal{X},P(X))$
• ${\mathcal{P}rob}_{Y|x}$: sub-cat. of $\mathcal{P}rob$ taking the form of $(\mathcal{Y},P(Y|x))$ with the conditional var. $x$.
• $\mathcal{S}tat$: cat. of The statistical models
• ${\mathcal{S}tat}_X$: cat. of The statistical models of the target rv $X$
• ${\mathcal{S}tat}_{Y|x}$: cat. of The statistical models of the target rv $Y|x$ with conditional var $x$.
• $\mathcal{B}ayes$: cat. of the Baysian models

$\mathcal{S}tat$ is regarded as a sub-cat. of $\mathcal{S}tat$ with the flatten priori. The Bayesian model gives joint $P(x,\theta )$。Therefore the category of the Bayesian models is a sub-cat. of $Prob$.

---

Estimator

Definition (Statistical model with an estimator)
model with estimator: $(M_{\theta },\hat{\theta }(X))$ where $\hat{\theta }:{\mathcal{X}}^N\to \Theta$, $X$ is a sample with size $N$.

In most case, we use MLE. The estimator has been implied by model.

---

Statistical Learning

supervised learning (determinant form):
$(\mathcal{X},\mathcal{Y},P(Y|X))$ where $X$ is input (conditional var.), $Y$ is output

Supervised learning based on sample $X=\{X_i\}$, is identified with statistical model:
$$({\mathcal{Y}}^N,P(Y|X)=\prod _{i}P(y_i|x_i))$$
where the sample $X$ is fixed, named design var. (design matrix, if it forms a matrix) and $Y$ is a sample point (sample with size 1).

I claim: statistical learning == conditionalized statistics (model)

---

Facts in statistical learning are also facts in statistics

Bias-Variance Decomposition in statistics: Error = Bias + Variance; in statistical learning: Error = Bias + Variance under condition of input variable;

---

Classical Models in Statistical Learning(SL)

• Supervised Learning
  • Regression: $P(Y|X)$, Linear Regression, Ridge/LASSO Regression ($X$ is the conditional rv)
  • Classification: $P(Y|X)$, Logistic Regression/LDA(/QDA)/Naive Bayesian Classifier
• Unsupervised Learning
  • Clustering: $P(X,Z)$, where $Z$ is unobservable, K-means/GMM
  • Dimension Reduction: $P(X,Z)$, PCA/ICA/MNF
  • Latent Variable Models: $P(X,Z)$, Mixed models(GMM), pLSA
  • Hidden Markov Model: $P^{\ast }(X_{1:T},Z_{1:T})$ where $(X_t,Z_t)\sim P$
• Others
  Time sequence: $P^{\ast }(X_{1:T})$, ARMA

---

Learner

A learner is an estimator for statistical model:
$$(M_{\theta },\hat{\theta }(X))$$
where $M_{\theta }$ is a statistical model.

One can define a latent model as $(P(X,Z),\hat{\theta }(X))$ for unsupervised learning; $(P(X,Y),\hat{\theta }(X,Y))$ for supervised learning.

---

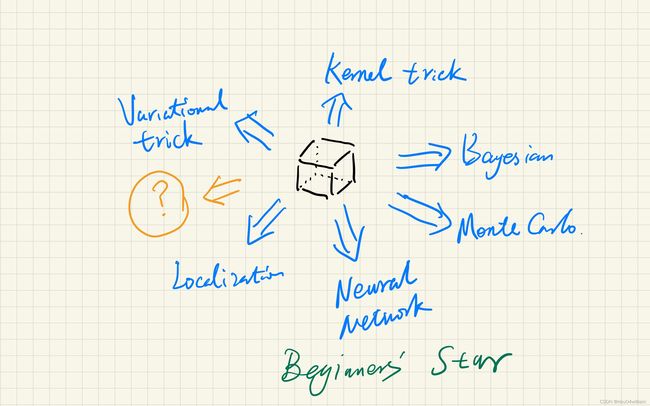
Beginners’ Magic Cube

The classical models are all categories. And we have a diagram about them. I’d like to call it “the beginners’ magic cube”, since it looks like a cube and the beginner of SL should learn them first.

---

Probabilitic Graph Model

Another way to describe the statistical (learning) model.

• Bayesian Network: Directed acyclic graph
• Markov Network(Random Field): Undirected graph

---

Methods

Methods as Functors:

• Kernel trick: $X\to \varphi (X)$
• Localization/Smoothing: ${\sum }_{i}K(x_0,x_i)l(x_i,y_i)$
• Hierarchical model: $P(X,Z_1,\cdots ,Z_n,Y)$ where $X\to Z_1\to \cdots \to Z_n\to Y$ forms Markov chain usually and $Z_1,\cdots ,Z_n$ are hidden.
• Variational trick: $(P(X,Z),Q(Z|X))$ where $Q(Z|X)$ is the variational distr.
• Neural network(NN): $f(x)\to Net(x)$
• Stochastic method/Monte Carlo method: Important sampling/MCMC

---

Advanced Models I:

Neural Models: Models equipped with Neural Networks; apply neural network in statistical models.

• Neural Models: MLP, embed NN into regression models
• RNN/LSTM: as a conditional HMM implemented by NN
• Neural Autoencoder: NLPCA, embed NN into the autoencoder
• Probabilistic Neural Autoencoder: Variational Autoencoder(VAE; the stochastic perturbation affacts the outputs of the layers)
• Stochastic NN: Dropout(the stochastic perturbation affacts the weights of the layers)
• Normalization Flow: Reparameterization, as a non-stochastic hierarchical VAE
• Hierarchical VAE: Diffusion Model/Consistency Model

---

Beginners’ Star

---

Create an advanced models I

Take VAE as an example

$$\begin{gathered} P(X)\sim N(\mu ,{\sigma }^2)\to P(X|Z)\sim N(f(z),{\sigma }^2),P(Z)\sim N(0,1) \\ \to (P(X,Z),Q(Z|X=x)\sim N(g(x),h(x))) \\ \to (P(X,Z),Q(Z|X=x)=g(x)+\xi h(x)),\xi \sim N(0,1) \end{gathered}$$

Write it in the style of the composition of functors (informally)
$VAE(f,g,h)=\mathrm{Rep}\circ \mathrm{Var}\circ \mathrm{LVM}(P(X))$, regarding functions $f,g,h$ as parameters.

The implimentation of VAE by the following NN (with a regularizing term):
$$y\sim f(g(x)+h(x)\xi ),$$
through self-supervised learning with data $\{(x_i,x_i)\}$, where $f,g,h$ are all neural layers, $\xi \sim N(0,1)$ is the perturbation variable of the hidden layer $g$. when $\xi \to 0$, $Q$ is degenerated, and VAE degenerates to an ordinary NN $f(g(x))$.

---

Create an advanced models II

Take RNN as an example

$$\begin{gathered} P(Y)\to \cdots \to P^{\ast }(Y,Z|X) \\ \to y_t=Net(x_t,z_{t-1}),z_t=Net(x_t,z_{t-1}) \end{gathered}$$

say $RNN(w)=\mathrm{NN}\circ \mathrm{TS}\circ \mathrm{Condi}\circ \mathrm{LVM}(P)$.

Homework

1. What about $Z_k\sim B(p_k)$ (multivariate Bernoullian distr.)
2. To create time sequence version of VAE

---

Advanced Models II

• Ensemble Learning
• Transfer Learning
• Incremental Learning(Continual Learning、On-line Learning)
• Life-Long Learing

Possible definition of Transfer Learning

• $(P(X|{\theta }_1),P(X|{\theta }_2)),{\theta }_1,{\theta }_2\sim P(\theta |\alpha )$
• $(P(X|{\theta }_1,{\theta }_0),P(X|{\theta }_2,{\theta }_0))$
• $(P(\varphi (X)|\theta ),P(\varphi (X)|\theta ))$
  with sample $X_1$ from sorce domain and sample $X_2$ from target domain

---

Misc.

• Reinforcement Learning: Stochastic Learning
  evaluation/sampling-estimation alternating.
  $\theta \to v\to \theta \to v\to \cdots$
• BiLSTM/BiLM/ELMo
• Transformer/Self-attention
• models based on Unnormalized distr. (Energy-based models)

Inspired by BiLSTM/BiLM: Tied Model
$(P(X|{\theta }_1,{\theta }_0),P(X|{\theta }_2,{\theta }_0))$ with the same sample.

Tied likelihood: $P(X|{\theta }_1,{\theta }_0)P(X|{\theta }_2,{\theta }_0)$
(a sort of pseudo-likelihood; a product of expert without normalized coef.)

---

Future Works

---

References

• PETER MCCULLAGH WHAT IS A STATISTICAL MODEL? The Annals of Statistics. 2002, 30(5): 1225–1310
• Jared Culbertson and Kirk Sturtz. Bayesian Machine Learning via Category Theory, 2013.
• Categories for AI. https://www.youtube.com/watch?v=4poHENv4kR0
• Kenneth A. Lloyd, Jr. A Category-Theoretic Approach to Agent-based Modeling and Simulation, 2010.
• Dan Shiebler, Bruno Gavranovic, Paul Wilson, Category Theory in Machine Learning, 2021.

---

链接: https://pan.baidu.com/s/1GdPiVGG3GIKVS4nWqlBm-w?pwd=1111 提取码: 1111