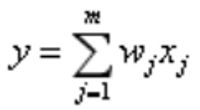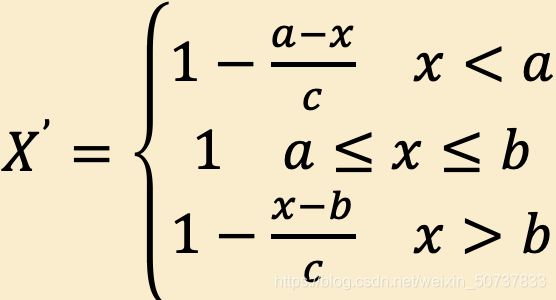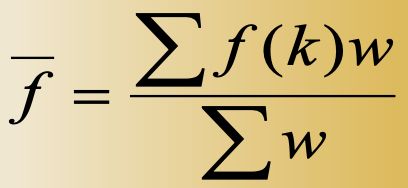综合评价方法
文章目录
-
- 1. 历年试题分析
-
- 1.1. 试题主要方向
- 1.2. 试题主要趋势
- 1.3. 创新
- 1.4. 问题与方法
- 2. 综合评价模型
-
- 2.1. 术语
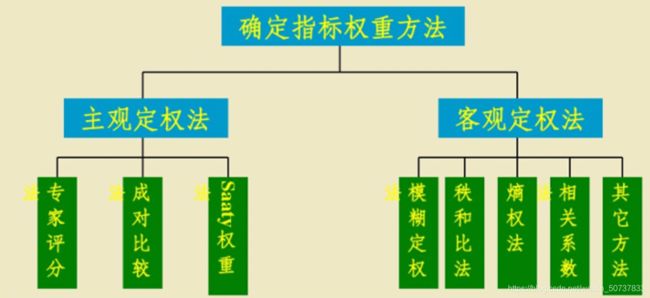
- 2.2. 综合评价方法分类
- 2.3. 综合评价基本概念
- 2.4. 评价指标
-
- 2.4.1. 评价指标的选取
- 2.4.2. 确定各评价指标的权值
- 2.4.3. 综合评价模型
- 2.5. 指标预处理
-
- 2.5.1. 指标一致化处理
- 2.5.2. 指标无量纲化
- 2.5.3. 定性指标的量化方法
- 3. 几种常用的综合评价方法
-
- 3.1. 计分法
-
- 3.1.1. 综合计分法
- 3.1.2. 排队计分法
- 3.2. 综合指数法
- 3.3. 功效系数法
- 3.4. Topsis法(包含计算流程)
- 4. 模糊综合评价
-
- 4.1. 评价步骤
- 4.2. 信息熵法(客观判断属性权重)
- 4.3. 算子的概念(用于权重向量与评判矩阵计算)
- 4.4. 结果选择
- 4.5. 思想和原理
- 4.6. 模型和步骤
- 5. 层次分析法(AHP)
-
- 5.1. 职员晋升案例
-
- 5.1.1. 层次结构图
- 5.1.2. 成对比较矩阵和特征向量
- 5.1.3. 一致性指标和一致性检验
- 5.1.4. 综合权重
- 5.1.5. 比较尺度(1-9)
- 5.2. 层次分析法的基本理论
- 5.3. 层次分析法的若干问题
-
- 5.3.1. 应用特点
- 5.3.2. 正互反阵最大特征根和特征向量的简化计算
- 5.3.3. 不完全层次结构的计算
- 5.3.4. 优缺点分析
1. 历年试题分析
1.1. 试题主要方向
- 优化(1)
- 评价(2)
- 预测(3)
1.2. 试题主要趋势
- 综合性:综合利用不同类型知识
- 分析性:侧重于对题目的分析
- 数据性:涉及到大数据处理
(例)评价方法分类:
- 主观赋权法
- 客观赋权法
1.3. 创新
- 新颖的解题切入点(如采用独有的数据,高效的不平常的数据)
- 数据来源有理有据(找数据)
- 合理运用算法模型
- 合理的问题假设(对题目进行模型以及条件的假设)
- 论文的写作必须图表兼备
1.4. 问题与方法
- 问题是主角,方法是配角
- 针对问题寻找适用的方法(优先选择可以讲的清的模型结构,尽量不去选择高大上但不懂的模型)
2. 综合评价模型
2.1. 术语
- 评价:按一定标准对客观实体对评价
- 指标:对象某一方面情况的特征依据
- 指标体系:多个相关评价指标组成的有机整体
- 综合评价:通过数学模型整合多个指标为一个综合评价
2.2. 综合评价方法分类
- 综合评定法(专家打分、加权、AHP、模糊神经网络)
- 两两比较法:顺序法、优序法
综合评价问题的分类:
- 分类:对对象进行分类(不局限于简单归纳)
- 比较排序:对全部评价单位综合排序
- 考察某一目标的综合实现程度:在有参考系的情况下做出整体评价
2.3. 综合评价基本概念
这类问题又称为多属性(或多指标)的综合评价问题。
(根据系统属性判断评价对象的优劣)
-
被评价对象
一个系统中选取多个被评价对象
-
评价指标
多个指标构成的度量量。
-
权重系数
用于区分各评价指标之间的重要性
当完全确定了评价对象之后,评价结果就完全依赖权重系数了。
-
综合评价模型
多个评价指标综合成的一个整体的评价指标
-
评价者
参与评价的人
2.4. 评价指标
2.4.1. 评价指标的选取
- 代表性:指标能够很好的代表对应层次
- 确定性:指标的数值有确定的高低的意义
- 灵敏性:指标值有一定的波动范围
- 独立性:指标尽量保证无法替代,有多个类似的选取几个,或聚类。
难以量化时:
- 系统分析法:凭经验按属性、类别划分。
- 文献资料分析优选法:全面查找属性优缺点资料,分析并取舍。
客观筛选:
- 逐个指标进行检验:有资料的基础上,分组并挑选有统计意义的指标。
- 多元回归与逐步回归:多元回归挑选回归系数大,或偏回归系数假设检验有显著性大;逐步回归自动挑选主要影响指标的功能。
- 指标聚类法:将多个指标通过聚类合并成一个指标。
如果有相关的文献,尽量选取广泛运用的指标。
可以更多的选择多种方法都可以使用的指标,适用于换方法。
选取指标时先列举需要属性类型,再对照类型进行列举属性。
在确认属性类型时重要的是:不要缩小题目意思的范围,应该发散思考。
2.4.2. 确定各评价指标的权值
确定权值都具有一定的主观性,每种方法都依赖于较为合理的专业解释。
2.4.3. 综合评价模型
2.5. 指标预处理
2.5.1. 指标一致化处理
指标类型:
- 极大型指标:值越大越好
- 极小型指标:值越小越好
- 中间型指标:一般要求取不大不小
- 区间型指标:有上下界范围
我们一般会选择将所有的指标统一为一种指标。(如极小型变成极大型)
所以我们采用一致化操作(一致化即为将指标类型变为一致)
一致化方法:
-
倒数一致化:取原数据的倒数。
优点:简单方便效果还行;
缺点:因为会把所有>1的值统一到0~1之间,会改变原始数据的分散程度,对综合评价不利。(但是结合后面的归一化操作可以弥补缺点)
-
减法一致化:用一个值减去原数据的值。
优点:不改变分散程度,效果更加稳定;
缺点:一般也不知道用什么值去减
-
以上两个用于极小型极大化。
-
中间型极大化:
极大化公式:X’ = 1 - |X - Xbest| / M;
Xbest 是最佳取值,M为指标可能取值和最佳取值的最大距离。
-
区间型最大化:
其中[a, b]为x的最佳稳定区间,c = max(a - m, M - b),M和m分别为x可能取值的最大值和最小值。
2.5.2. 指标无量纲化
无量纲化处理又称为指标数据的标准化,或规范化处理。抵消单位,消除数据单位限制。
常用方法:标准差方法、极值差方法和功效系数方法等。
处理方法:
-
极差标准化法:
公式:X’ = (X - Xmin) / (Xmax - Xmin);
(指标的最大值 Xmax 和最小值 Xmin 和观察值 X )特点:处理后每个数值变化范围都变成了[0-1];
缺点:有新数据加入会造成最值变化,需要重算。
-
Z-score标准化法(标准差标准化法):
操作方法:X’ = (x - x均) / SD;
特点:结果成正态分布,基本都在[-3 - 3]之间
-
功效系数法:
功效系数法:
公式:x’ij = c + (xij - mj) / (Mj - mj) * d (i = 1, 2, …, n; j = 1, 2, …, n);
c为平移量,d为放缩量。用于修改区间位置与大小(一般好看用)。
线性比例标准化法:
- 极大化法:X’ = X / Xmax (X ≥ 0);
- 极小化法:X’ = Xmin / X (X ≥ 0);
缺点:都不适用于X < 0;因为是非线性的改变,会影响原始指标之间的相互关系。
log函数标准化法:
公式:X’ = log10X / log10 Xmax(观察值 X,指标最大值 Xmax);
特点:方法要求X ≥ 1,有压缩数据差异的功能。
反正切函数标准化法:
公式:X’ = arctan(X) * 2 / π;
特点:具有放大数据差异的作用
最常用的方法:
- 极差标准化法
- Z-score标准化法
2.5.3. 定性指标的量化方法
根据实际问题,构造模糊隶属函数的量化方法是一种可行有效的方法
计算方法:
假设:定义评价因素分为五个等级:A, B, C, D, E;对应5, 4, 3, 2, 1;
注解:a, b, å, ß都是待定常数,根据对应等级和隶属度代入计算得出。
(隶属度:表示一个模糊概念中的程度,如有50%的秃头,隶属度为0.5)补充:隶属模型是表示一个模糊集合的真实程度。一般没有固定的模型,隶属模型很多是依靠“学习”完成的。
3. 几种常用的综合评价方法
-
现有的统计方法:主要为多元统计方法,如多元回归、逐步回归分析、判别分析、因子分析、时间序列分析。
-
模糊多元分析方法:模糊数学发展而来,如模糊聚类、模糊判别、模糊综合评价。
-
简易方法:综合评分法、综合指数法、Topsis法、秩和比法。
特点:简单实用、适用性广、存在一定局限性。
3.1. 计分法
3.1.1. 综合计分法
方法:按比例分配分值,累加计分。
缺点:简便易行,过于粗糙。
3.1.2. 排队计分法
将评价单位的各项评价指标依优劣秩序排队,再将名次(位置)转化为单项评价值,最后由单项评价值计算各单位的综合评价值(总分)。
K为名次(1~n),f(K)为单项评价值(0~100),f均为综合评价值(0~100)

(然后调整评价值区间,材料会好看一点)
优点:
- 方法简单
- 不用找其他的简单标准
- 评价值的值域统一
- 适用范围广(可用于定序以上层次的数据)
缺点:
- 原始数据的信息损失多
3.2. 综合指数法
概念:
-
指数:变量对值的相对数
-
个体指数:反映事物或现象动态变化的指数
计算方法:
- 高优指标:p = X / M(实测值 X,标准值 M)
- 低优指标:p = M / X(实测值 X,标准值 M)
(高优,低优表示越高越好和越低越好)
-
总指数:反映多种事物或现象动态平均变化程度的指数
比较复杂,没有统一的表达形式,常见的有加权求和,算数平均,乘积法。
-
综合指数法:综合总指数形式对现象进行分析的方法
缺点:在某项参数特别突出时会造成很大的影响。
适用范围:适用于被评价对象差异不大,各评价指标单项波动范围也不大的情况。
3.3. 功效系数法
公式:(实际值 - 不容许值)/ (满意值 - 不容许值)* 40 + 60;
优点:考虑的每个指标的数值,相较于指数法,缩小了单项评价的差距,减弱了突出项的影响,但效果距离排队计分法还是差很多。
3.4. Topsis法(包含计算流程)
意思为:与理想方案相似性的顺序选优技术(多决策分析的常用方法)。
方法:基于归一化后的矩阵,通过比较各评价对象与最优方案的相对接近程度,评价优劣。
计算过程:
- 选取对象与评价指标,设置一个矩阵;
- 对高优,低优指标进行同向化,归一化;
- 得到归一化矩阵并获取最优+最劣向量;
- 用平方差公式分别求出对象与最优/最劣向量的距离;
- 求接近程度 Ci = Di- / (Di+ + Di-)。(重要!!!)
选取结果接近程度 C 的值越高,则结果越接近最优方案。
4. 模糊综合评价
模糊概念:一个没有明确非0即1的分界线的形容词,如胖瘦。
模糊数学的基本思想:用程度代替属于/不属于(非0即1),如某人秃头的程度为0.5。
4.1. 评价步骤
- 确定评价对象的因素集;
- 确定评语集;
- 对单个因素评价;
- 进行综合评价。
4.2. 信息熵法(客观判断属性权重)
原理:
- 在信息论中,熵为不确定性的指标;
- 按照归一化矩阵,信息熵法表示为每一种属性之间的概率分布是否一致,如果过于一致,则权重小。如三种汽车的款式所带来的效益一模一样,则说明款式这个属性的权重就不会很高。
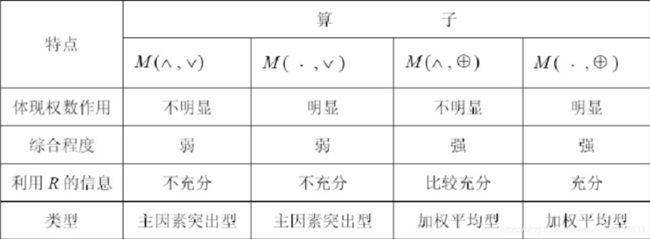
4.3. 算子的概念(用于权重向量与评判矩阵计算)
其中算子就是表示数据的算法:当1*3和3*4的矩阵是用算子计算是,列计算用前者,行计算用后者(计算是就是如果给先计算的打括号,括号里面的就是前者。
经过计算后可以得到模糊评判向量。
4.4. 结果选择
- 最大隶属原则(最大的就能代表结果)
- 加权平均原则(用平均值根据所有人情况确定结果)
4.5. 思想和原理
基本思想:用属于程度代替属于或不属于.刻画“中介状态”
基本原理:
- 首先确定指标和评价集;
- 再分别确定各个因素的权重及它们的隶属度矢量,获得模糊评判矩阵;
- 最后进行模糊运算并进行归一化,得到评价结果
特点:被评价对象有唯一的评价值,不受对象集合的影响.
4.6. 模型和步骤
因素集 -> 评判集 -> 单因素评判 -> 综合评判
-
确定因素集
找到多种因素并将每种因素划分开来
-
确定评语集
划分等级并由评价者进行评价
-
确认权重向量
-
单因素模糊评价
通过隶属度得到模糊关系矩阵。并进行归一化处理,平方差等于1。
-
根据合适方法对结果分析
优点:
- 对模糊概念得出了科学的量化评价
- 评价结果是矢量,信息丰富,可以进一步加工
缺点:
- 计算复杂,指标权重主观性强。
- 指标集基数大时会导致隶属度小,会产生误差以至于不匹配等现象(超模糊现象),无法分辨。(可用分层模糊估计法加以改进)
5. 层次分析法(AHP)
5.1. 职员晋升案例
AHP是职员晋升问题的的一种常用方法。
另一种常用方法是多属性决策方法。
职员晋升问题:根据职员多方面的表现,给每个职员做一个排序。
(本方法均以职员晋升问题作分析)
特点:
- 针对经济、社会等主观因素大,难以量化的情况;
- 在实际运用、处理问题、计算方法方面和多属性决策有许多相似;
- 定性与定量相结合的,系统化、层次化的分析方法。
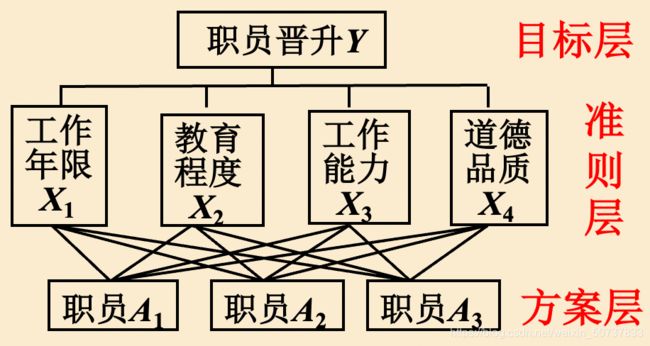
5.1.1. 层次结构图
层次结构图,毋庸置疑当然是指将模型结构分为多层咯。
分层:自下而上分为目标、准则、方案三层。
分层结构:
- 目标层:确定单个准则对多个目标的权重,也就是职员在一种属性中的排名;
- 准则层:确定方案对准则的权重,也就是属性的权重;
- 方案层:综合前两种确定方案对目标的权重,也就是结果每个职员的权重。
5.1.2. 成对比较矩阵和特征向量
构建成对比较矩阵:
- 定义在每个属性中,每个对象的权重;
- 将多个属性权重向量构成矩阵(用重要性比构建矩阵)
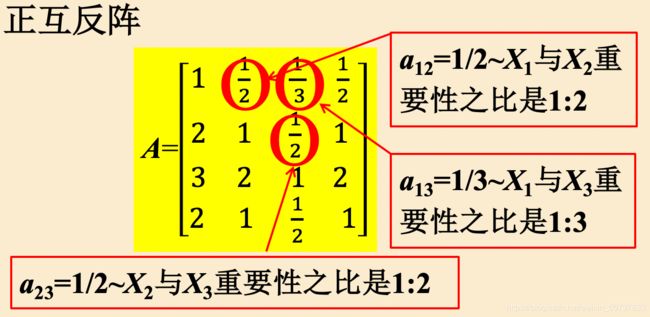
- 但属性比例并不一定要符合比例规范:属性1和属性2的比例为1:2,属性2和属性3的比例也为1:2,但属性1和属性3不一定要1:4(比例只要是在一定容许范围内就可以了,AHP容许成对比较存在不一致,并确定了这种不一致的容许范围)。
- 沿主对角线互为倒数,不要问我为什么。
特征向量:
- 成对比较矩阵满足aij * ajk = aik;
- 一致阵:各列均相差一个因子;
- 一致阵性质:秩为1,唯一非0特征根为n,每一列向量都是对应于n的特征向量。
- 为什么将一致阵,是为下面计算服务的~
- 如果成对比较矩阵不满足一致阵条件,但在容许范围之内,则可以先归一化再使用。
5.1.3. 一致性指标和一致性检验
-
n阶正互反阵A的最大特征根 lambda ≥ n,A是一致阵的充要条件为 lambda = n;
-
一般我们的矩阵是 lambda 必 ≤ n,对吧?所以只要 lambda 比n大的越多,说明误差越大,太大了就说明超出了容许范围;
-
用 lambda - n 衡量正互反阵 A 的不一致程度;
-
Saaty定义**一致性指标**:CI = (lambda - n) / (n - 1) —— CI = 0时A是一致阵,CI越大A越不一致;
-
然后Saaty引入一组随机指标RI(RI是确定一个n阶标准正互反阵,随机在 1~9 和 1/1, 1/2, ~, 1/9 取值后,求一致性指标 CI 的均值为 RI),Saaty给出:
n 3 4 5 6 7 8 9 10 RI 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 -
所以我们定义一致性比率 CR = CI / RI,当 CR < 0.1 时就通过一次性检验了。
备注:一致性检验通过后就可以直接归一化矩阵得到指标权重向量了。
5.1.4. 综合权重
- 计算出方案对准则的权重,并通过一致性检验,得到权重向量;
- 计算出目标对准则(3个职员对4个准则)的权重,通过一致性检验并得到权重,同时也为有3个职员4个准则,我们可以得到3*4对权重矩阵。
- 最后我们就可以简单的加权和:结果对象的权重 = 方案对准则的权重 * 准则对目标的权重。
- 推广:现在是3层结构,如果是S层呢?很简单,就是把每一层的关系求出来,然后加权和就行了。如有1,2,3,4,5这五层,我们求出12,23,34,45间的关系,加权和就能得到15的关系了(我们都知道,1就是给定的条件,5就是我们的结果~
5.1.5. 比较尺度(1-9)
上面我们讲到用比较的方法输出两个属性之间的差别。比如1:2,1:3之类的。
这里我们给定一个比较标准:
| 尺度aij | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Xi和Xj对Y重要性 | 相同 | 稍强 | 强 | 明显强 | 绝对强 |
5.2. 层次分析法的基本理论
步骤:
- 先构成多层的层次结构;
- 构建上下层之间的成对比较阵;
- 计算每个成对比较阵的特征根和特征向量,做一致性检验;
- 将各层进行综合,就可以计算最下层对最上层的权重咯
5.3. 层次分析法的若干问题
5.3.1. 应用特点
- 处理问题类型:决策、评价、分析、预测;
- 建立模型要有主要决策层参与;
- 构建成对比较阵的数量依据,要由强专家给出。
5.3.2. 正互反阵最大特征根和特征向量的简化计算
一致阵的每一列向量都是特征向量,一致性在容许范围内的正互反阵的列向量都近似特征向量,可取其某种意义下的平均。
流程:
- 得到成对比较阵;
- 列归一化得到归一化矩阵(列为属性);
- 求行的算术平均值(行为对象);
- 再用Aw = lambda*w求出特征值就好了。
5.3.3. 不完全层次结构的计算
不完全,也就是说有些之间没有关系呗,没关系不就是0?
略了略了
5.3.4. 优缺点分析
优点:
- 系统性:按照分解、比较、判断、综合的思维方式进行决策——系统分析;
- 实用性:定性定量结合;
- 简洁性:计算简单,方便
缺点:
- 囿旧:无法产生新方案;
- 粗略:将定性定量,结果粗糙;
- 主观:主观作用大,难以服人