数据结构 线性表-单链表的定义及基本操作
文章目录
- 一.引入
- 二.线性表链式存储结构的定义
-
- 2.1 顺序结构和链式结构的区别
- 2.2 结点定义
- 2.3 头指针与头结点
-
- 2.3.1头指针与头结点的定义
- 2.3.2头结点与头指针的异同
- 三.单链表的基本操作
-
- 3.1单链表的初始化
- 3.2 单链表的建立
-
- 3.2.1头插法
- 3.2.2 尾插法
- 3.2.3两种方法总结
- 3.3单链表的插入操作
- 3.4单链表的删除操作
- 3.5单链表的查找
-
- 3.5.1按位查找
- 3.5.2按值查找
- 3.6单链表的销毁
- 四.总结
一.引入
对于线性表来说,有顺序存储结构,然而顺序结构是有缺点的:插入和删除时需要移动大量元素;因此我们需要解决这一系列问题,线性表的链式存储结构刚好解决了这些问题。
二.线性表链式存储结构的定义
2.1 顺序结构和链式结构的区别
在顺序结构中,每个数据元素只需要存数据元素信息就可以了,在链式结构中,除了要存储元素信息外,还要存储后继元素的存储地址,因此,我们引入了结点。
2.2 结点定义
为了表示每个数据元素 a 与其直接后继数据元素 air1 之间的逻辑关系,对数据元素 a来说,除了存储其本身的信息之外,还需存储一个指示其直接后继的信息(即直接后继的存储位置)。把存储数据元素信息为数据域,存储直接后继位置的域称为指针域,指针域中存储的信息称做指针或链。这两部分信息组成数据元素a的存储映像,称为结点 。多个结点链接成我们的链表。
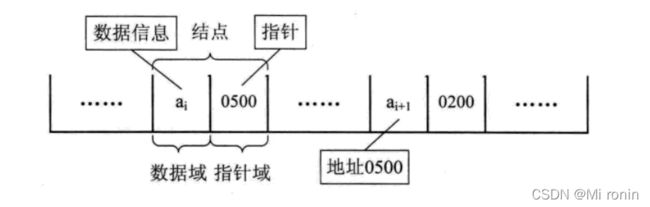
结点的描述:
typedef struct LNode{ //定义单链表结点类型
int data; //数据域,可以是别的各种数据类型,本文统一用int类型
struct LNode *next; //指针域
}LNode, *LinkList;
2.3 头指针与头结点
2.3.1头指针与头结点的定义
通常我们把链表中第一个结点的存储位置叫做头指针,整个链表的存取就从头指针开始进行,一般来说最后一个,意味着直接后继不存在了,所以我们规定,线性链表的最后一个结点为空。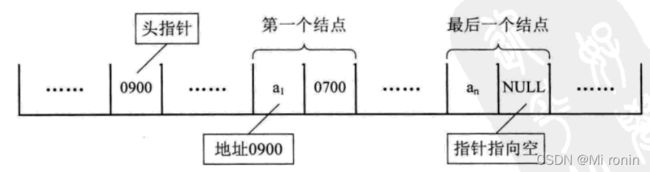
为了更方便对链表的操作,我们会在单链表的第一个结点前设置一个结点,称为头结点。
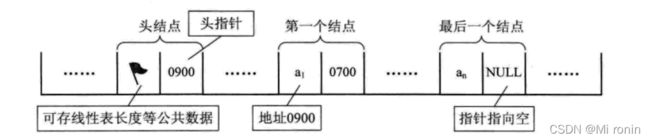
一般来说头结点的数据域可以不存储任何信息,头结点的指针域存储指向第一个结点的指针。
2.3.2头结点与头指针的异同
| 头指针 | 头结点 |
|---|---|
| 头指针是指向第一结点的指针,链表有头结点是指向头结点的指针 。 | 头结点是为了便于操作设立的,在第一元素的结点前,数据域一般没有意义。 |
| 头指针有标识作用,常用头指针冠以链表名字。 | 有了头结点,对于第一元素结点前的插入删除操作统一了。 |
| 无论链表是否为空头指针不为空。头指针是链表的必要元素 | 头结点不一定是链表必要元素。 |
三.单链表的基本操作
3.1单链表的初始化
单链表的初始化就是申请一个头结点,将指针域置空。
LinkList LinkListInit()
{
LNode *L;
L = (LNode *)malloc(sizeof(LNode)); //申请结点空间
if(L == NULL) //判断是否有足够的内存空间
printf("申请内存空间失败\n");
L->next = NULL;
}
3.2 单链表的建立
对于单链表的建立我们有两种创建方法,分别为:头插法和尾插法。
3.2.1头插法
头插法简单理解就是始终让新结点在第一的位置,示意图如下:

头插法的算法思路:
- 声明一个指针p;
- 初始化一个空链表L;
- 建立一个带头结点的单链表;
- 生成一个新结点赋值给p,将p的数据域赋值,将p插入到头结点与前一新结点之间。
代码如下:
void CreatListHead(LinkList *L,int n)
{
LinkList p;
int i;
srand(time(0));
*L=(LinkList)malloc(sizeof(LNode));
(*L)->next=NULL;
for(i=0;i<n;i++)
{
p=(LinkList)malloc(sizeof(LNode));
p->data=rand()%100+1;
p->next=(*L)->next;
(*L)->next=p;
}
}
头插法最重要的是这两行代码:
p->next=(*L)->next;//将头指针所指向的下一个结点地址赋给新结点next
(*L)->next=p; //将新创建的结点的地址赋给头指针的下一个结点
3.2.2 尾插法
尾插法顾名思义就是把每次新结点插在终端结点的后面,示意图如下:

尾插法的算法思路:
- 首先初始化一个单链表;
- 声明一个尾指针r,让r始终指向当前链表的尾结点;
- 循环向单链表的尾部插入新的结点*s,将尾指针r的next域指向新结点;
- 修改尾指针r指向新结点,也就是当前链表的尾结点;
- 最后别忘记将尾结点的指针域置空。
代码如下:
void CreatListtTail(LinkList *L,int n)
{
LinkList p,r;
int i;
srand(time(0));
*L=(LinkList)malloc(sizeof(LNode));
r=*L;
for(i=0;i<n;i++)
{
p=(Node *)malloc(sizeof(LNode));
P->data = rand()%100+1;
r->next=p; //表尾终结结点的指针指向新结点
r=p; //将当前的新结点定义为表尾终端结点
}
r->next = NULL;
}
尾插法重要代码:
r->next=p;//表尾终结结点的指针指向新结点
r=p; //将当前的新结点定义为表尾终端结点
我们需要注意L与r的关系,r会随着循环不断变化结点,而L则是随着循环增长为一个多结点的链表。
3.2.3两种方法总结
- 头插法相对简便,但插入的数据与插入的顺序相反;
- 尾插法操作相对复杂,但插入的数据与插入顺序相同。
根据自己需求来使用不同的方法。
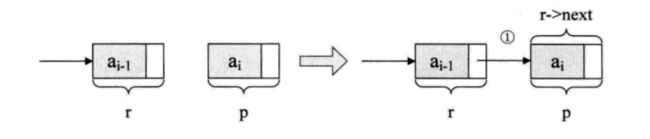
3.3单链表的插入操作
插入操作只需要将p的后继结点改成s的后继结点,再把s变成p的后继结点。

算法思想:
从表头开始遍历,查找第 i-1个结点,即插入位置的前驱结点为p,然后令新结点s的指针域指向p的后继结点,再令结点p的指针域指向新结点*s。
代码如下:
void Insert(LinkList &L, int i, int x){
LNode *p = GetElem(L,i-1);
LNode *s = (LNode *)malloc(sizeof(LNode));
s->data = x;
s->next = p->next;
p->next = s;
}
核心为:
s->next=p->next;
p->next=s;
注意: 这两句的顺序不可以进行交换。
假如交换后就会导致拥有a(i+1)数据元素的结点没了上级,这样的插入操作是无效的。
3.4单链表的删除操作
删除操作只需把p的后继结点改成p的后继的后继结点。
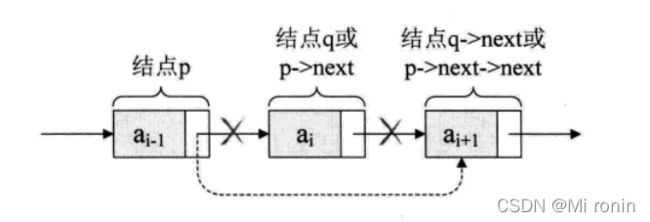
算法思想:
- 声明一指针p指向链表头指针,初始j从1开始;
- j<1时,遍历链表让指针p向后移,不断指向下一个结点,j累加1;
- 若末尾p为空,则说明第i个接点不存在;
- 否则成功,将p->next赋值给q;
- 将q结点中的数据赋值给e,作为返回;
- 释放q 。
代码如下:
void Delete(LinkList *L, int i,int *e)
{
int j;
linklist p,q;
p=*l;
j=1;
while(p->next&&j<1)
{
p=p->next;
++j;
}
if(i<1 || i>Length(L))
return error;
q=p->next;
p->next=q->next;
*e=q->data;
free(q);
}
核心如下:
p->next=q->next;
3.5单链表的查找
3.5.1按位查找
查找单链表中中第 i 个位置的元素。
算法思想:
- 声明一个指针p指向链表的第一个结点,初始化j;
- j<1,遍历链表,让p的指针向后移动,不断指向下一个结点,j累加;
- 若末尾p为空,则说明第i个接点不存在;
- 否则查找成功,返回p的数据。
代码如下:
LNode *GetElem(LinkList L, int i){
int j=1;
LNode *p = L->next;
if(i==0)return L;
if(i<1)return NULL;
while(p && j<i){
p = p->next;
j++;
}
return p; //如果i大于表长,p=NULL,直接返回p即可
}
说白了其实就是从前向后挨个寻找,直到第i个结点为止。
3.5.2按值查找
查找值x在单链表L中的结点指针。
算法思想:
从单链表的第一个结点开始,依次比较表中各个结点的数据域的值,若某结点数据域的值等于x,则返回该结点的指针;若整个单链表中没有这样的结点,则返回空。
代码如下:
LNode *LocateElem(LinkList L, int x){
LNode *p = L->next;
while(p && p->data != x){
p = p->next;
}
return p;
}
3.6单链表的销毁
这里千万要注意的是,动态分配的内存是需要我们手动去回收的,所以要养成一个好的习惯,在程序的必要位置回收那些动态分配的内存。
算法思想:
- 声明一结点p和q;
- 将第一个结点赋值给p;
- 将下一结点赋值给q,释放p,将q赋值给p。
代码如下:
Status ClearList(LinkList *L)
{
LinkList p,q;
p=(*L)->next;
while(p)
{
q=p->next;
free(p);
p=q;
}
(*L)->next=NULL;
return OK;
}
四.总结
对于单链表来说,我们需要将一系列操作的核心思想理解并牢记,这样会对后续数据结构的学习有所帮助。
(小白一位,如有错误欢迎指正)