01-线性回归sklearn实现

一、传统方式绘制直线并计算斜率

（1）绘制一条直线

（2）已知两点，绘制一条直线

（3）已知两点，求直线斜率

二、利用sklearn线性回归求直线斜率

sklearn.linear_model.LinearRegression

sklearn.datasets.make_regression

三、糖尿病数据集的线性回归分析

四、岭回归的参数调节

参数调节

岭迹分析-模型系数的可视化比较

五、LASSO回归

LASSO回归的参数调节

一、传统方式绘制直线并计算斜率

（1）绘制一条直线

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(-6,6,100)
y=0.5*x+2
plt.figure()
plt.plot(x,y,color='red')
plt.show()

（2）已知两点，绘制一条直线

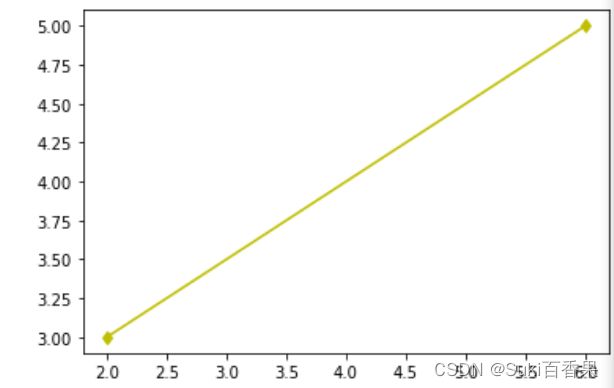
x=np.array([2,6])
y=np.array([3,5])
plt.plot(x,y,'yd-')
plt.show()

（3）已知两点，求直线斜率

k=(y[1]-y[0])/(x[1]-x[0])
print(k)

二、利用sklearn线性回归求直线斜率

sklearn.linear_model.LinearRegression

LinearReagression(
'fit_intercept=True'  #节距是否使用

'normalize=False'   #标准化

'copy_x=True'         #复制x,是否覆盖原始的x

'n_jobs=None'        #计算时设置的任务个数（-1表示使用所有的CPU）

)#大部分取默认值

属性

coef_         输出系数，没有截距

intercept_  输出截距

rank_         输出矩阵的秩

singular     矩阵X的奇异值，仅在x为密集矩阵时有效

方法

fit(self,X,y[,sample_weight])         #训练模型，sample_weight为每个样本的权重值

predict(self,X)                               #模型预测，返回预测值

score(self,X,y['sample_weight])    #模型pinggu，放回R^2系数，最优质为1，说明所有数据都预测正确

get_params（self['deep]）           #deep默认为True，返回超参数的值

set_params(self.** params)          #修改超参数的值
 

利用线性回归求通过平面上两点（2,3）（6,5）的直线斜率

#利用线性回归求通过平面上两点（2,3）（6,5）的直线斜率
from sklearn.linear_model import LinearRegression
x=np.array([2,6])
y=np.array([3,5])
x=x.reshape(-1,1)
#实例化
lr=LinearRegression()
lr.fit(x,y)
print("过两点(2,3)与(6,5)的直线斜率为:{},截距项为:{:.2f}".format(lr.coef_,lr.intercept_))

Out：过两点(2,3)与(6,5)的直线斜率为:[0.5],截距项为:2.00

#模型预测
x_test=np.array([3,4,5]).reshape(-1,1)
y_predict=lr.predict(x_test)
y_predict

Out：array([3.5, 4. , 4.5])

#模型评估--计算R 方值
lr.score(x,y)

Out：1.0

#计算模型的均方误差
from sklearn.metrics import mean_squared_error
y=0.5*x_test+2
mean_squared_error(y,y_predict)

Out：6.573840876841765e-32

模型效果不错，输出结果基本约等于0

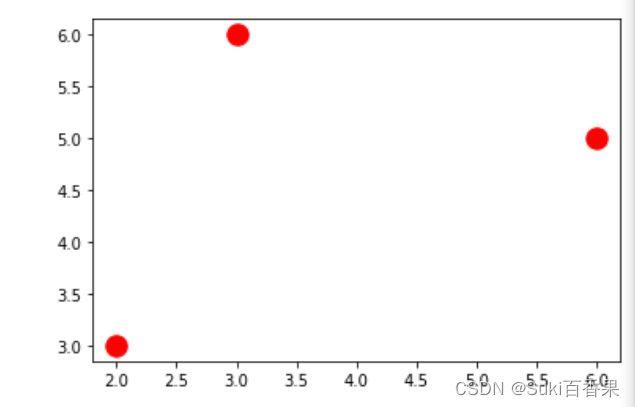
假设有第三个点，坐标为（3,6）

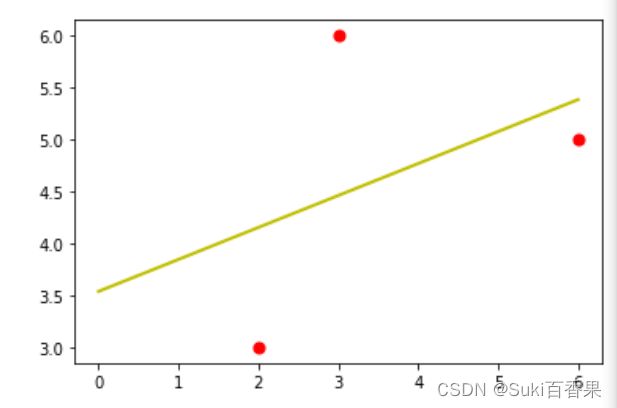
#假设有第三个点，坐标为（3,6）
x2=np.array([[2],[3],[6]])
y2=np.array([3,6,5])
#绘制三个点的散点图
plt.scatter(x2,y2,s=180,c='r')

lr_2=LinearRegression()
lr_2.fit(x2,y2)
z=np.linspace(0,6,100)
z_predict=lr_2.predict(z.reshape(-1,1))
plt.plot(z,z_predict,lw=2,c='y')
plt.scatter(x2,y2,s=50,c='r')

#计算r方系数
lr_2.score(x2,y2)

Out：0.17582417582417564

#均方误差
y2_predict=lr_2.predict(y.reshape(-1,1))
from sklearn.metrics import mean_squared_error
mean_squared_error(y2,y2_predict)

Out：1.3767258382643

sklearn.datasets.make_regression

属性

n_samples:样本数

n_features:特征数（自变量个数）

n_informative:参与建模特征数

n_targets:因变量个数

noise:噪音

bias:偏差（截距）

coef:是否输出coef标识

random_state:随机状态若为固定值则每次产生的数据都一样

利用sklearn生成100条具有1个特征的回归分析数据集

from sklearn.datasets import make_regression
X_3,y_3=make_regression(n_samples=100,n_features=1)
plt.scatter(X_3,y_3)

 数据太过于整齐，可以更改参数来分散数据

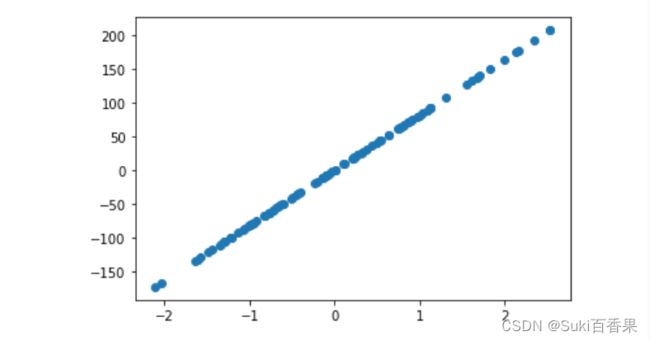
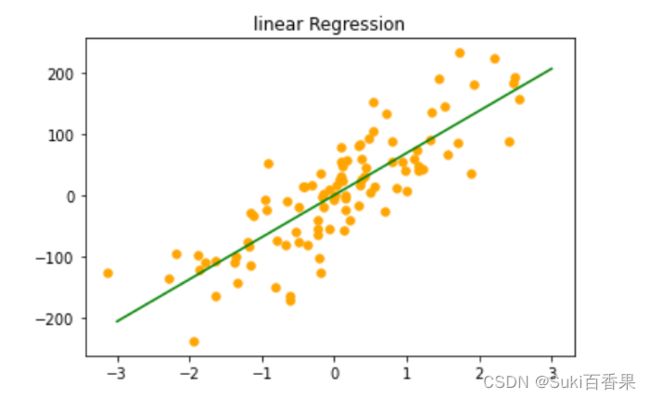
X_3,y_3=make_regression(n_samples=100,n_features=1,noise=50,random_state=8)
plt.scatter(X_3,y_3)

#利用线性回归模型对数据X_3,y_3进行拟合
#模型实例化
reg=LinearRegression()
#模型训练
reg.fit(X_3,y_3)
#绘制回归直线
z=np.linspace(-3,3,200).reshape(-1,1)
plt.scatter(X_3,y_3,c='orange',s=30)
plt.plot(z,reg.predict(z),c='g')
plt.title("linear Regression")

 拟合回归直线，得到下图

print('回归直线的斜率是：{:.2f}，回归直线的截距是：{:.2f}'.format(reg.coef_[0],reg.intercept_))

可以得出回归直线的斜率和截距

Out：回归直线的斜率是：68.78，回归直线的截距是：1.25

三、糖尿病数据集的线性回归分析

首先导入sklearn中的糖尿病数据集

from sklearn.datasets import load_diabetes
diabetes=load_diabetes()
print(diabetes['DESCR'])

设置特征变量和因变量

X=diabetes.data#特征变量
y=diabetes.target#因变量

划分训练集和测试集

#划分训练集合测试集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=8)

lr=LinearRegression().fit(X_train,y_train)
print("训练集得分:{:.2f}，测试集得分为:{:.2f}".format(lr.score(X_train,y_train),lr.score(X_test,y_test)))

Out：训练集得分:0.53，测试集得分为:0.46

根据训练集和测试集得分可知，模型并不太好。

四、岭回归的参数调节

**sklearn.linear_model.Ridge**

_L2正则化_

**Ridge**(
alpha=1.0 #正则化因子

fit_intercept=True #截距

normalize=False #标准化

copy_X=True #是否覆盖X

max_iter=None #最大迭代次数

tol=0.001 #忍耐度，提升的数值不大时停止迭代

solver='auto' #一些解析方法

random_state=None #随机种子)

from sklearn.linear_model import Ridge
#模型实例化
ridge=Ridge()
#模型实例化+模型训练
ridge.fit(X_train,y_train)
print("训练集得分:{:.2f}，测试集得分为:{:.2f}".format(ridge.score(X_train,y_train),ridge.score(X_test,y_test)))

Out：训练集得分:0.43，测试集得分为:0.43

参数调节

#alpha=10
ridge10=Ridge(alpha=10).fit(X_train,y_train)
print("训练集得分:{:.2f}，测试集得分为:{:.2f}".format(ridge10.score(X_train,y_train),ridge10.score(X_test,y_test)))

out：训练集得分:0.15，测试集得分为:0.16

#alpha=0.1
ridge01=Ridge(alpha=0.1).fit(X_train,y_train)
print("训练集得分:{:.2f}，测试集得分为:{:.2f}".format(ridge01.score(X_train,y_train),ridge01.score(X_test,y_test)))

out：训练集得分:0.52，测试集得分为:0.47

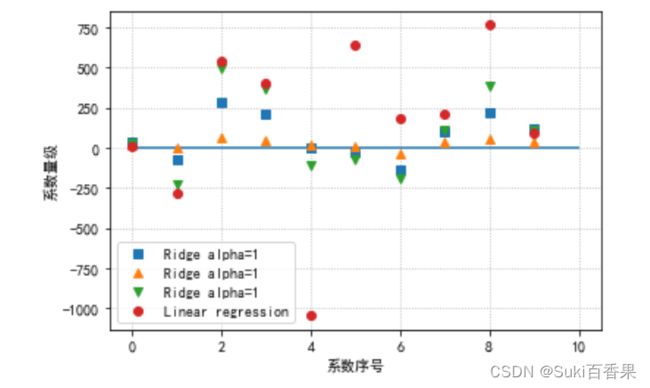
岭迹分析-模型系数的可视化比较

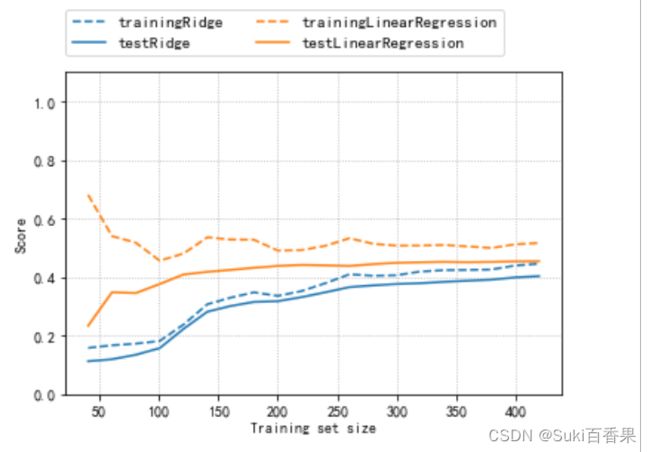
#中文
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False 
#模型系数的可视化比较
plt.plot(ridge.coef_,'s',label='Ridge alpha=1')
plt.plot(ridge10.coef_,'^',label='Ridge alpha=1')
plt.plot(ridge01.coef_,'v',label='Ridge alpha=1')
plt.plot(lr.coef_,'o',label='Linear regression')
plt.xlabel("系数序号")
plt.ylabel("系数量级")
#0,0直线
plt.hlines(0,0,len(lr.coef_))
plt.legend(loc='best')
plt.grid(linestyle=':')

#绘制学习曲线：取固定的alpha值，改变训练集的数据量
from sklearn.model_selection import learning_curve,KFold
def plot_learning_curve(est,X,y):
    training_set_size,train_scores,test_socres=learning_curve(
        est,X,y,train_sizes=np.linspace(.1,1,20),cv=KFold(20,shuffle=True,random_state=1))
    estimator_name=est.__class__.__name__
    line = plt.plot(training_set_size,train_scores.mean(axis=1),'--',
                  label='training'+estimator_name)
    plt.plot(training_set_size,test_socres.mean(axis=1),'-',
             label='test'+estimator_name,c=line[0].get_color())
    plt.xlabel('Training set size')
    plt.ylabel('Score')
    plt.ylim(0,1.1)
plot_learning_curve(Ridge(alpha=1),X,y)
plot_learning_curve(LinearRegression(),X,y)
plt.legend(loc=(0,1.05),ncol=2,fontsize=11)
plt.grid(linestyle=':')

 

 

五、LASSO回归

**sklearn.linear_model.Lasso**

**Lasso**(

alpha=1.0 #正则化因子

fit_intercept=True #截距

normalize=False #标准化

precompute=False

copy_X=True #是否覆盖X

max_iter=None #最大迭代次数

tol=0.001 #忍耐度，提升的数值不大时停止迭代

warm_start=False#是否重新开始，默认从头开始

solver='auto' #一些解析方法

random_state=None #随机种子)

from sklearn.linear_model import Lasso
lasso=Lasso()
lasso.fit(X_train,y_train)
print("训练集得分:{:.2f}，测试集得分为:{:.2f}".format(lasso.score(X_train,y_train),lasso.score(X_test,y_test)))

Out ：训练集得分:0.36，测试集得分为:0.37

LASSO回归相对于岭回归更适合做特征选择

LASSO回归的参数调节

#增加最大迭代次数的默认设置
lasso=Lasso(max_iter=10000)
lasso.fit(X_train,y_train)
print("训练集得分:{:.2f}，测试集得分为:{:.2f}".format(lasso.score(X_train,y_train),lasso.score(X_test,y_test)))
#特征选择
print("套索回归使用的特征数：{}".format(np.sum(lasso.coef_ !=0)))

Out：训练集得分:0.36，测试集得分为:0.37

          套索回归使用的特征数：3

          套索回归使用的特征数：3

正则化越大，特征数越少

#增加最大迭代次数的默认设置（默认max_iter=1000）
#同时调整alpha的值
lasso01=Lasso(alpha=0.1,max_iter=100000).fit(X_train,y_train)
print("alpha=0.1时，训练集得分:{:.2f}，测试集得分为:{:.2f}".format(lasso01.score(X_train,y_train),lasso01.score(X_test,y_test)))
print("套索回归使用的特征数：{}".format(np.sum(lasso01.coef_ !=0)))

Out：alpha=0.1时，训练集得分:0.52，测试集得分为:0.48

         套索回归使用的特征数：7

#调整alpha的值为0.0001
lasso00001=Lasso(alpha=0.0001,max_iter=100000).fit(X_train,y_train)
print("alpha=0.1时，训练集得分:{:.2f}，测试集得分为:{:.2f}".format(lasso00001.score(X_train,y_train),lasso00001.score(X_test,y_test)))
print("套索回归使用的特征数：{}".format(np.sum(lasso00001.coef_ !=0)))

 Out：alpha=0.1时，训练集得分:0.52，测试集得分为:0.48

           套索回归使用的特征数：7

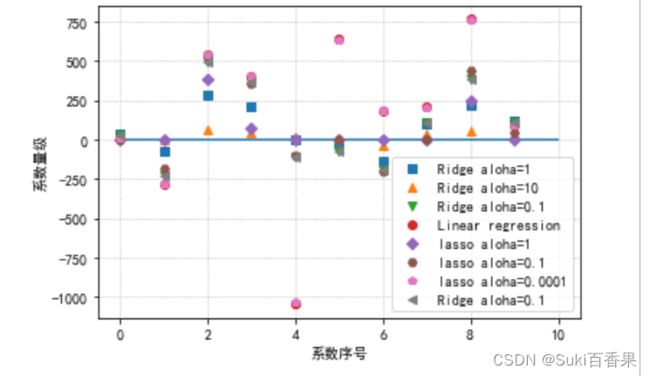
#模型系数的可视化比较
plt.plot(ridge.coef_,'s',label='Ridge aloha=1')
plt.plot(ridge10.coef_,'^',label='Ridge aloha=10')
plt.plot(ridge01.coef_,'v',label='Ridge aloha=0.1')
plt.plot(lr.coef_,'o',label='Linear regression')

plt.plot(lasso.coef_,'D',label='lasso aloha=1')
plt.plot(lasso01.coef_,'H',label='lasso aloha=0.1')
plt.plot(lasso00001.coef_,'p',label='lasso aloha=0.0001')
plt.plot(ridge01.coef_,'<',label='Ridge aloha=0.1')

plt.xlabel("系数序号")
plt.ylabel("系数量级")
plt.hlines(0,0,len(lr.coef_))
plt.legend(loc='best')
plt.grid(linestyle=':')
#中文
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False