《动手学深度学习》学习笔记(三)
第三章 深度学习基础
一、线性回归
模型:基于输入计算输出的表达式。![]()
训练模型:通过数据来寻找特定的模型参数值,使模型在数据上的误差尽可能小的过程。找到表达式的参数w1和w2以及b。
训练数据:真实数据样本(sample)。标签标注(label)。预测标签的两个因素叫做特征(feature)。特征用来表征样本的特点。
损失函数:衡量表达式预测值和真实值之间的误差。最小二乘法。
训练模型就是希望基于训练数据找到一组模型参数,来使训练样本的损失函数最小。
优化算法:当模型和损失函数简单时,可求最小化问题的解析解。当表达式复杂时或许没有解析解,或者无法求出。只能通过优化算法有限次迭代模型参数来尽可能的降低损失函数的值。这类解叫做数值解。在求数值解的优化算法中,小批量随机梯度下降在深度学习中被广泛使用。算法:
- 先选取一组模型参数的初始值,如随机选取:正态分布。
- 接下来对参数进行多次迭代,使每次迭代都有可能降低损失函数的值。
- 在每次迭代中,先随机均匀采样一个由固定数目训练数据样本所组成的小批量(mini-batch)B,
- 然后求小批量中数据样本的平均损失有关模型参数的导数。
- 最后用此结果与预先设定的一个正数(步长-学习率)的乘积作为模型参数在本次迭代的减小量。
模型预测:模型训练好后,对新数据进行预测。
采用矢量加法的方式要比向量按元素逐一做标量加法更快速。
线性回归的简洁实现
1、生成数据集:
其中features是训练数据特征,labels是标签。
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.tensor(np.random.normal(0, 1, (num_examples, num_inputs)), dtype=torch.float)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)2、读取数据:
PyTorch提供了data包来读取数据。
import torch.utils.data as Data
batch_size = 10
# 将训练数据的特征和标签组合
dataset = Data.TensorDataset(features, labels)
# 随机读取小批量
data_iter = Data.DataLoader(dataset, batch_size, shuffle=True)3、定义模型:
PyTorch提供了大量预定义的层,这使我们只需关注使用哪些层来构造模型。
导入torch.nn模块。实际上,“nn”是neural networks(神经网络)的缩写。顾名思义,该模块定义了大量神经网络的层。之前我们已经用过了autograd,而nn就是利用autograd来定义模型。nn的核心数据结构是Module,它是一个抽象概念,既可以表示神经网络中的某个层(layer),也可以表示一个包含很多层的神经网络。在实际使用中,最常见的做法是继承nn.Module,撰写自己的网络/层。一个nn.Module实例应该包含一些层以及返回输出的前向传播(forward)方法。
class LinearNet(nn.Module):
def __init__(self, n_feature):
super(LinearNet, self).__init__()
self.linear = nn.Linear(n_feature, 1)
# forward定义前向传播
def forward(self, x):
y = self.linear(x)
return y
net = LinearNet(num_inputs)
print(net) # 使用print可以打印出网络的结构。输出:
LinearNet(
(linear): Linear(in_features=2, out_features=1, bias=True)
)事实上我们还可以用nn.Sequential来更加方便地搭建网络,Sequential是一个有序的容器,网络层将按照在传入Sequential的顺序依次被添加到计算图中。
# 写法一
net = nn.Sequential(
nn.Linear(num_inputs, 1)
# 此处还可以传入其他层
)
# 写法二
net = nn.Sequential()
net.add_module('linear', nn.Linear(num_inputs, 1))
# net.add_module ......
# 写法三
from collections import OrderedDict
net = nn.Sequential(OrderedDict([
('linear', nn.Linear(num_inputs, 1))
# ......
]))
print(net)
print(net[0])输出:
Sequential(
(linear): Linear(in_features=2, out_features=1, bias=True)
)
Linear(in_features=2, out_features=1, bias=True)
可以通过net.parameters()来查看模型所有的可学习参数,此函数将返回一个生成器。
for param in net.parameters():
print(param)输出:
Parameter containing:
tensor([[-0.0277, 0.2771]], requires_grad=True)
Parameter containing:
tensor([0.3395], requires_grad=True)注意:
torch.nn仅支持输入一个batch的样本不支持单个样本输入,如果只有单个样本,可使用input.unsqueeze(0)来添加一维。
4、初始化模型:
在使用net前,我们需要初始化模型参数,如线性回归模型中的权重和偏差。PyTorch在init模块中提供了多种参数初始化方法。这里的init是initializer的缩写形式。我们通过init.normal_将权重参数每个元素初始化为随机采样于均值为0、标准差为0.01的正态分布。偏差会初始化为零。
from torch.nn import init
init.normal_(net[0].weight, mean=0, std=0.01)
init.constant_(net[0].bias, val=0) # 也可以直接修改bias的data: net[0].bias.data.fill_(0)注:如果这里的
net是用3.3.3节一开始的代码自定义的,那么上面代码会报错,net[0].weight应改为net.linear.weight,bias亦然。因为net[0]这样根据下标访问子模块的写法只有当net是个ModuleList或者Sequential实例时才可以,详见4.1节。
5、定义损失函数:
PyTorch在nn模块中提供了各种损失函数,这些损失函数可看作是一种特殊的层,PyTorch也将这些损失函数实现为nn.Module的子类。我们现在使用它提供的均方误差损失作为模型的损失函数。
loss = nn.MSELoss()6、定义优化算法:
同样,我们也无须自己实现小批量随机梯度下降算法。torch.optim模块提供了很多常用的优化算法比如SGD、Adam和RMSProp等。下面我们创建一个用于优化net所有参数的优化器实例,并指定学习率为0.03的小批量随机梯度下降(SGD)为优化算法。
import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.03)
print(optimizer)输出:
SGD (
Parameter Group 0
dampening: 0
lr: 0.03
momentum: 0
nesterov: False
weight_decay: 0
)我们还可以为不同子网络设置不同的学习率,这在finetune时经常用到。例:
optimizer =optim.SGD([
# 如果对某个参数不指定学习率,就使用最外层的默认学习率
{'params': net.subnet1.parameters()}, # lr=0.03
{'params': net.subnet2.parameters(), 'lr': 0.01}
], lr=0.03)有时候我们不想让学习率固定成一个常数,那如何调整学习率呢?主要有两种做法。
- 一种是修改
optimizer.param_groups中对应的学习率, - 另一种是更简单也是较为推荐的做法——新建优化器,由于optimizer十分轻量级,构建开销很小,故而可以构建新的optimizer。
但是后者对于使用动量的优化器(如Adam),会丢失动量等状态信息,可能会造成损失函数的收敛出现震荡等情况。
# 调整学习率
for param_group in optimizer.param_groups:
param_group['lr'] *= 0.1 # 学习率为之前的0.1倍7、训练模型:
在训练模型时,我们通过调用optim实例的step函数来迭代模型参数。按照小批量随机梯度下降的定义,我们在step函数中指明批量大小,从而对批量中样本梯度求平均。
num_epochs = 3
for epoch in range(1, num_epochs + 1):
for X, y in data_iter:
output = net(X)
l = loss(output, y.view(-1, 1))
optimizer.zero_grad() # 梯度清零,等价于net.zero_grad()
l.backward()
optimizer.step()
print('epoch %d, loss: %f' % (epoch, l.item()))输出:
epoch 1, loss: 0.000457
epoch 2, loss: 0.000081
epoch 3, loss: 0.000198
分别比较学到的模型参数和真实的模型参数。我们从net获得需要的层,并访问其权重(weight)和偏差(bias)。学到的参数和真实的参数很接近。
dense = net[0]
print(true_w, dense.weight)
print(true_b, dense.bias)输出:
[2, -3.4] tensor([[ 1.9999, -3.4005]])
4.2 tensor([4.2011])小结:
torch.utils.data模块提供了有关数据处理的工具,torch.nn模块定义了大量神经网络的层,torch.nn.init模块定义了各种初始化方法,torch.optim模块提供了很多常用的优化算法。
二、softmax回归
线性回归模型适用于输出为连续值的情景。对于输出为图像类别这样的离散值的预测:采用softmax回归。
softmax回归的输出单元从一个变成了多个,且引入了softmax运算使输出更适合离散值的预测和训练。与线性回归的一个主要不同在于,softmax回归的输出值个数等于标签里的类别数。
softmax实现了归一化。运算不改变预测类别输出。argmax(oi)
同时,离散数值分类往往采用交叉熵损失函数,不再采用平方损失函数。
最小化交叉熵损失函数等价于最大化训练数据集所有标签类别的联合预测概率。
softmax将预测概率最大的类别作为输出类别。如果与真实类别标签一致,说明这次预测是正确的。所以往往采用准确率(accuracy)来评价模型的表现。等于正确预测数量与总预测数量之比。
三、图像分类数据集Fashion-MNIST
图像分类数据集中最常用的是手写数字识别数据集MNIST[1]。但大部分模型在MNIST上的分类精度都超过了95%。为了更直观地观察算法之间的差异,我们将使用一个图像内容更加复杂的数据集Fashion-MNIST。(这个数据集也比较小,只有几十M,没有GPU的电脑也能吃得消)。
本节我们将使用torchvision包,它是服务于PyTorch深度学习框架的,主要用来构建计算机视觉模型。torchvision主要由以下几部分构成:
torchvision.datasets: 一些加载数据的函数及常用的数据集接口;torchvision.models: 包含常用的模型结构(含预训练模型),例如AlexNet、VGG、ResNet等;torchvision.transforms: 常用的图片变换,例如裁剪、旋转等;数据增强。torchvision.utils: 其他的一些有用的方法。工具集
1、获取数据集:
首先导入本小结需要的包或模块:
import torch
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import time
import sys
sys.path.append("..") # 为了导入上层目录的d2lzh_pytorch
import d2lzh_pytorch as d2l下载数据集:
mnist_train = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST', train=True, download=True, transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST', train=False, download=True, transform=transforms.ToTensor())通过torchvision.datasets来下载数据集。第一次调用时会从自动从网上获取数据。我们通过参数train来指定获取训练集或测试集。
另外我们还指定参数transform = transform.ToTensor()使所有数据转换为Tensor,如果不进行转换则返回的是PIL图片。transforms.ToTensor()将尺寸为 (H x W x C) 且数据位于[0, 255]的PIL图片或者数据类型为np.uint8的NumPy数组转换为尺寸为(C x H x W)且数据类型为torch.float32且位于[0.0, 1.0]的Tensor。自动完成了归一化。(此处归一化需要核实)。
上面的mnist_train和mnist_test都是torch.utils.data.Dataset的子类,所以我们可以用len()来获取该数据集的大小,还可以用下标来获取具体的一个样本。训练集中和测试集中的每个类别的图像数分别为6,000和1,000。因为有10个类别,所以训练集和测试集的样本数分别为60,000和10,000。
print(type(mnist_train))
print(len(mnist_train), len(mnist_test))输出:
60000 10000 我们可以通过下标来访问任意一个样本:
feature, label = mnist_train[0]
print(feature.shape, label) # Channel x Height x Width输出:
torch.Size([1, 28, 28]) tensor(9)需要注意的是,
feature的尺寸是 (C x H x W) 的,而不是 (H x W x C)。第一维是通道数,因为数据集中是灰度图像,所以通道数为1。后面两维分别是图像的高和宽。
Fashion-MNIST中一共包括了10个类别,分别为t-shirt(T恤)、trouser(裤子)、pullover(套衫)、dress(连衣裙)、coat(外套)、sandal(凉鞋)、shirt(衬衫)、sneaker(运动鞋)、bag(包)和ankle boot(短靴)。以下函数可以将数值标签转成相应的文本标签。
# 本函数已保存在d2lzh包中方便以后使用
def get_fashion_mnist_labels(labels):
text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
return [text_labels[int(i)] for i in labels]下面定义一个可以在一行里画出多张图像和对应标签的函数。
# 本函数已保存在d2lzh包中方便以后使用
def show_fashion_mnist(images, labels):
d2l.use_svg_display()
# 这里的_表示我们忽略(不使用)的变量
_, figs = plt.subplots(1, len(images), figsize=(12, 12))
for f, img, lbl in zip(figs, images, labels):
f.imshow(img.view((28, 28)).numpy())
f.set_title(lbl)
f.axes.get_xaxis().set_visible(False)
f.axes.get_yaxis().set_visible(False)
plt.show()现在,我们看一下训练数据集中前10个样本的图像内容和文本标签。
X, y = [], []
for i in range(10):
X.append(mnist_train[i][0])
y.append(mnist_train[i][1])
show_fashion_mnist(X, get_fashion_mnist_labels(y))2、读取小批量:
数据读取经常是训练的性能瓶颈,特别当模型较简单或者计算硬件性能较高时。PyTorch的
DataLoader中一个很方便的功能是允许使用多进程来加速数据读取。这里我们通过参数来设置4个进程读取数据。
mnist_train是torch.utils.data.Dataset的子类,所以我们可以将其传入torch.utils.data.DataLoader来创建一个读取小批量数据样本的DataLoader实例。
batch_size = 256
if sys.platform.startswith('win'):
num_workers = 0 # 0表示不用额外的进程来加速读取数据
else:
num_workers = 4
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)该函数将返回train_iter和test_iter两个变量。
最后我们查看读取一遍训练数据需要的时间。
start = time.time()
for X, y in train_iter:
continue
print('%.2f sec' % (time.time() - start))输出:
1.57 sec四、多层感知机
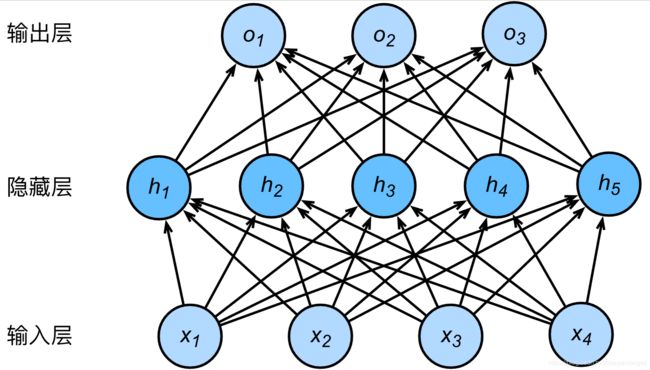
多层感知机在单层神经网络的基础上引入了一到多个隐藏层(hidden layer)。隐藏层位于输入层和输出层之间。
综上,只是增加隐藏层,实际上还是等价于一个单层神经网络。嵌套而已。
上述问题的根源在于全连接层只是对数据做仿射变换(affine transformation),而多个仿射变换的叠加仍然是⼀个仿射变换。解决问题的⼀个⽅法是引⼊⾮线性变换,例如对隐藏变量使⽤按元素运算的⾮线性函数进⾏变换,然后再作为下⼀个全连接层的输⼊。这个⾮线性函数被称为激活函数(activation function)。
所以说:从感知机到多层感知机的进步在于:1、激活函数。sigmoid,ReLU,tanh函数。2、隐藏层。
多层感知机就是含有至少一个隐藏层的由全连接层组成的神经网络,且每个隐藏层的输出通过激活函数进行变换。多层感知机的层数和各隐藏层中隐藏单元个数都是超参数。
五、模型选择、欠拟合和过拟合、权重衰减、丢弃法
训练误差,泛化误差。独立同分布假设。于该独立同分布假设,给定任意一个机器学习模型(含参数),它的训练误差的期望和泛化误差都是一样的。
由于无法从训练误差估计泛化误差,一味地降低训练误差并不意味着泛化误差一定会降低。
权重衰减:正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小,是应对过拟合的常用手段。通常会使学到的权重参数的元素较接近0。
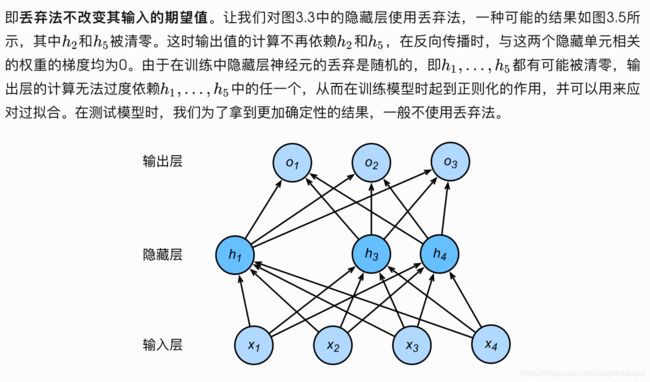
使用丢弃法:由于在训练中隐藏单元的丢弃是随机的,即h1,...,h5都有可能被清零,输出层的计算无法过度依赖h1,...,h5中的任一个,从而在训练模型时起到正则化的作用,并可以用来应对过拟合。
训练时,Dropout层将以指定的丢弃概率随机丢弃上一层的输出元素;在测试时即model.eval()后,Dropout层并不发挥作用。
六、正向传播、反向传播和计算图
1、正向传播
正向传播是指对神经网络沿着从输入层到输出层的顺序,依次计算并存储模型的中间变量(包括输出)。
输出为J称为有关给定数据样本的目标函数,带有正则化的损失函数。
2、反向传播
反向传播指的是计算神经网络参数梯度的方法。反向传播依据微积分中的链式法则,沿着从输出层到输入层的顺序,依次计算并存储目标函数有关神经网络各层的中间变量以及参数的梯度。
在模型参数初始化完成后,我们交替地进行正向传播和反向传播,并根据反向传播计算的梯度迭代模型参数。既然我们在反向传播中使用了正向传播中计算得到的中间变量来避免重复计算,那么这个复用也导致正向传播结束后不能立即释放中间变量内存。这也是训练要比预测占用更多内存的一个重要原因。这些中间变量的个数大体上与网络层数线性相关,每个变量的大小跟批量大小和输入个数也是线性相关的,它们是导致较深的神经网络使用较大批量训练时更容易超内存的主要原因。
小结
- 正向传播沿着从输入层到输出层的顺序,依次计算并存储神经网络的中间变量。
- 反向传播沿着从输出层到输入层的顺序,依次计算并存储神经网络中间变量和参数的梯度。
- 在训练深度学习模型时,正向传播和反向传播相互依赖。
七、数值稳定性和模型初始化
当神经网络的层数较多时,模型的数值稳定性容易变差。多层累积后容易出现衰减和爆炸(指数衰减和指数爆炸)的乘积。类似地,梯度的计算也更容易出现衰减或爆炸。
PyTorch中nn.Module的模块参数都采用了较为合理的初始化策略(不同类型的Layer采用不同的初始化方法。)
八、实战Kaggle比赛:房价预测
数据预处理:
标准化:将特征的每个值先减去均值再除以标准差得到标准化后的每个特征值。
缺值处理:对于缺失的特征值,我们将其替换成该特征的均值。
numeric_features = all_features.dtypes[all_features.dtypes != 'object'].index
all_features[numeric_features] = all_features[numeric_features].apply(
lambda x: (x - x.mean()) / (x.std()))
# 标准化后,每个数值特征的均值变为0,所以可以直接用0来替换缺失值
all_features[numeric_features] = all_features[numeric_features].fillna(0)
离散数值转化:将离散数值转成指示特征。举个例子,假设特征MSZoning里面有两个不同的离散值RL和RM,那么这一步转换将去掉MSZoning特征,并新加两个特征MSZoning_RL和MSZoning_RM,其值为0或1。如果一个样本原来在MSZoning里的值为RL,那么有MSZoning_RL=1且MSZoning_RM=0。
(类似one-hot编码形式,将离散值变换成多个值。变成了两个特征。)
# dummy_na=True将缺失值也当作合法的特征值并为其创建指示特征
all_features = pd.get_dummies(all_features, dummy_na=True)
all_features.shape # (2919, 331)特征数从79增加到了331。