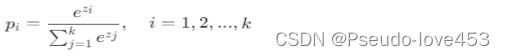列举四种神经网络激活函数的函数公式、函数图及优缺点和适用场景

1.阶跃函数

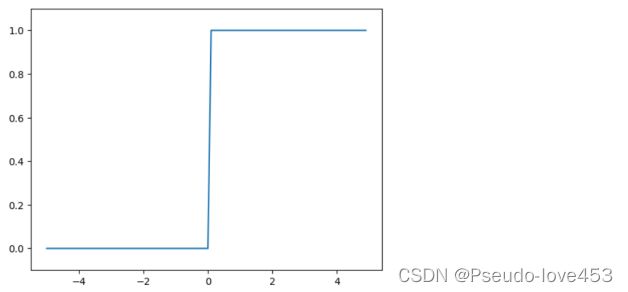
阶跃函数：这是一种最简单的非线性激活函数，它将小于零的值转换为0，大于零的值转换为1。虽然这个函数非常简单，但是它很少被使用，因为它在不同数据之间造成了不连续的跳跃，这会导致反向传播算法出现不可导的情况。

阶跃函数公式：

阶跃函数代码及函数图：

# 导入相关库
import numpy as np
import matplotlib.pyplot as plt

# 定义阶跃函数
def step_function(x):
    return np.array(x > 0, dtype=np.int)

# 生成输入数据
x = np.arange(-5.0, 5.0, 0.1)

# 计算输出数据
y = step_function(x)

# 绘制图像
plt.plot(x, y)
plt.ylim(-0.1, 1.1)  # 指定y轴的范围
plt.show()

 

优点：

①阶跃函数的输出只有两个取值，计算简单，容易理解。

②阶跃函数在负数区域为0，在正数区域为1，比较符合生物神经元的工作方式。

③阶跃函数的输出为稳定的0或1，对于二分类等问题（比如逻辑回归），可以起到决策边界的作用。

缺点：

①阶跃函数不存在导数，在某些神经网络算法（比如反向传播）中会导致计算困难；

②阶跃函数不连续，不平滑，一些优化算法会在其间出现震荡或收敛慢；

③阶跃函数的梯度为0或无限大，容易产生梯度消失或梯度爆炸问题。

适用场景：

①对于二分类问题，阶跃函数可以作为激活函数使用，起到判定正例还是反例的作用；

②在探索神经网络基础知识时，阶跃函数可以作为最简单的激活函数使用；

③在某些特殊的场景下，阶跃函数可能会有一些适用性。例如某些控制问题，人工神经元模拟等。

2.Sigmoid函数

Sigmoid函数：Sigmoid函数是一种常见的激活函数，它将输入值映射到（0，1）范围内，常用于二元分类问题或输出概率的场合。

Sigmoid函数公式：

Sigmoid函数代码及函数图：

# 定义Sigmoid函数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# 生成输入数据
x = np.arange(-5.0, 5.0, 0.1)

# 计算输出数据
y = sigmoid(x)

# 绘制图像
plt.plot(x, y)
plt.ylim(-0.1, 1.1)  # 指定y轴的范围
plt.show()

 

优点：

①Sigmoid函数的输出值在0到1之间，可以表示概率分布；

②Sigmoid函数的形状较为平滑，在梯度下降等优化算法中稳定性较好；

③Sigmoid函数在中心区域灵敏度比较高，可以起到压缩激活信号的作用。

缺点：

①Sigmoid函数在取值较大或较小的区域，梯度会非常小。这会导致梯度消失的问题。同时，梯度经过链式法则计算还会变得更小，这会导致梯度传播变得困难，影响神经网络训练的速度和效果。

②Sigmoid函数输出不是以0为中心的，需要进行平移和缩放才能与其他激活函数协同工作。

适用场景：

①Sigmoid函数常用于二分类问题，表示样本属于某一类别的概率；

②Sigmoid函数可用于生成器网络（generator），输出值应当在(0,1)之间；

③在某些需要平滑的回归任务中可以使用Sigmoid作为激活函数；

④在某些需要保持概率大小的神经网络结构中使用Sigmoid函数。

3.ReLU函数

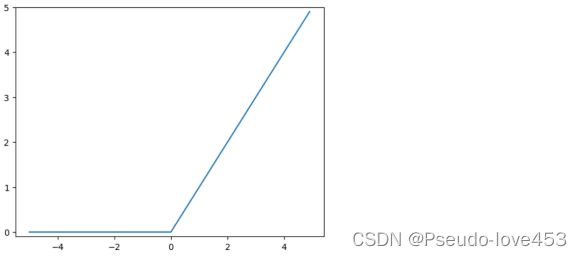
ReLU函数: ReLU函数是近年来深度学习中最新最流行的激活函数之一。它可以更好地对梯度传递进行处理，避免出现梯度消失的情况，并且计算效率更高。

ReLU函数公式：

ReLU函数代码及函数图：

# 定义Softmax函数
def softmax(x):
    exp_x = np.exp(x)
    return exp_x / np.sum(exp_x)

# 生成输入数据
x = np.array([1.0, 2.0, 3.0])

# 计算输出数据
y = softmax(x)

# 绘制图像
plt.bar(np.arange(len(y)), y)
plt.xticks(np.arange(len(y)), ["Class 1", "Class 2", "Class 3"])
plt.show()

 

优点：

①ReLU函数的计算简单，只需要取输入值和0的最大值即可，因此计算速度快；

②ReLU函数的导数在正半轴为常数1，在负半轴为常数0，计算起来简单，有助于加速反向传播算法的学习速度；

③ReLU函数在输入为正数时，能够有效抵消梯度消失（gradient vanishing）的问题，提高训练的速度和效果。

缺点：

①ReLU函数在负半轴输出为0，当输入为负数时可以导致神经元死亡（dead neuron）的问题，因此在某些情况下可能会影响训练效果；

②ReLU函数在输入为0时，导数不存在，因此训练时需要小心处理输入值为0的情况，避免训练失败；

③对于存在负数输入的情况，ReLU函数可能会产生“梯度爆炸（gradient explosion）”的问题。

适用场景：

①在深度神经网络中，由于ReLU函数在正半轴的输出为正数，对于减轻梯度消失问题（gradient vanishing）具有明显优势，因此常用于中间层的激活函数；

②对于输入为正数的情况，ReLU函数比Sigmoid和tanh等函数更为合适，可以加速神经网络模型的训练；

③ReLU函数通常用于卷积神经网络（CNN）中，有助于提高模型的求解速度和卷积层的效率。

4.Softmax函数

Softmax函数:是一种常用的激活函数，通常用于多分类问题中，将神经网络最后一层的输出转换为各类别的概率值。其主要作用是将神经网络的输出归一化到（0，1）之间，且保证所有类别的输出概率和为1。

Softmax函数公式：

Softmax函数代码及函数图：

# 定义Relu函数
def relu(x):
    return np.maximum(0, x)

# 生成输入数据
x = np.arange(-5.0, 5.0, 0.1)

# 计算输出数据
y = relu(x)

# 绘制图像
plt.plot(x, y)
plt.ylim(-0.1, 5)  # 指定y轴的范围
plt.show()

优点：

①Softmax函数能够把输出的各个类别映射为一个[0,1]之间的概率值，使输出结果更易解释；

②Softmax函数概率化输出，更能满足概率统计学的原理和实际应用需求；

③Softmax函数的导数和Hessian矩阵可以很容易地计算，这对于使用梯度下降算法进行模型训练来说是非常便捷的。

缺点：

①Softmax函数在指数运算过程中，可能存在计算上溢或下溢的问题；

②Softmax函数有较强的平移不变性（translation invariance），因此可能被感受野的变换和补偿所干扰，导致识别性能下降。

适用场景：

①Softmax函数常用于多分类问题，对于输出层的激活函数来说是一种常见的选择；

②在一些输出要求为概率值的场合，可以使用Softmax函数，如语音识别中的发音识别、图像分类中的物体识别等；

③在一些生成模型和强化学习中，Softmax函数常被作为生成过程中数据分布的一项重要工具，来生成随机样本序列、分配策略和抽取动作等。