光学系统中的几何像差及其对成像质量的影响

光学系统中的几何像差及其对成像质量的影响

光学几何的基本概念

光线、光束

由于光的衍射，想要从光源发出的光能中分离出光线来是不可能的，需要将此复杂的光学成像及光能传播问题简化。根据光的波动理论，由光源上一点发出的电磁波被看作是以波面的形式向四周推进，若光所处的介质为各向同性的均匀介质，则波面向各方向的传播速度相同，不同时刻的波面为一系列以发光点为中心的球面波(Spherical Wave)，光能就是沿着波面的法线方向传播的，此处几何光学中的光线即波动光学中波面的法线，因此我们将波面的法线束称为光束(Light Heam)。无限远处发光点发出的是平面波(Plane Wave)，对应于平行光束，有限远处发光点发出的是球面波，对应于同心的发散光束和汇聚光束，统称为同心光束。同心光束经透镜或有缺陷的光学系统以后会失去同心性，此时所对应的波面可能是轴对称或非轴对称的非球面。

衍射(Differaction)

当光传经小孔时，光的衍射现象将明显地表现出来，通过小孔的光除了按原来的直线方向继续传播外，还要向其他方向衍射光能，当波长为0时，才不存在衍射现象。

干涉(Interference)

从光源同一点发出的光经不同途径传播后再相遇于某点时，其合成作用应是电矢量的相加，而不是简单的光强度的相加，其强度可能加强，也可能是减弱的。

反射(Reflection)、折射(Refraction)

当光传播到两种介质的光滑分界面时，依界面的性质不同，光线返回原介质即为反射，光线进入另一介质即为折射。光在不同介质中的传播速度各不相同，在真空中光速最快，以$c$表示，介质的折射率便是描述光在该介质中的传播速度$v$减慢程度的物理量，为：
$$n=\frac{c}{v}\ge 1$$

费马原理(Fermat’s Principle)

费马原理从光程的观点来描述光的传播，所谓光程，是光在介质中所经过的几何路程$l$与该介质折射率$n$的乘积：
$$s=ln$$
由于$n=\frac{c}{v}、l=vt$，其中$t$为光传播的时间，即有：
$$s=ct$$

光程相当于光在在介质中走过$l$这段路程的时间$t$内，在真空中所走过的几何路程。光从一点到另一点是沿光程为极值的路径传播的，即光沿光程为极小、极大、常亮的路径传播，又称极端光程定律。

色散(Dispersion)

介质的折射率只是对单一波长的光而言，而波长反应了光的一种颜色。实际最长遇见的是白光的成像，白光是各种波长色光的复合光，除真空外，任何透明介质对不同波长的色光具有不同的折射率，随介质不同，折射率随波长而变的程度不同，这种性质称为光的色散(Dispersion)，通常的光学介质折射率随波长的变短而增大，尤其是短波长部分，折射率增加得更快，红光的波长长，折射率小，产生较小的偏角，紫光将产生较大的偏角。如果入射于折射棱镜的是白光，由于棱镜对不同色光具有不同折射率，各色光经折射后的折射角将不同，经整个棱镜后的偏角也随之不等，白光经棱镜折射后将分解成各色光而呈现一片按顺序排列的连续光谱(红、橙、黄、绿、青、蓝、紫)。

色散示意图

理想光学系统

所谓理想光学系统就是能对任意宽空间内的点以任意宽的光束成完善像的光学系统。

• 共轭点(Conjugate Points): 物空间中一点对应于像空间中唯一的一点，这一对对应点称为共轭点。

• 光轴(Optical Axis): 光学仪器中的光学系统由一系列折射和反射表面组成，主要是折射球面，各表面曲率中心均在同一直线上的光学系统为共轴光学系统(Symmetrical Optical System)，这条直线为光轴，实际光学系统大部分属于共轴光学系统。

• 焦距(Focal Length): 光线从物体所侧照射到薄透镜上，并以平行光束进入透镜，光束被透镜折射，并聚焦到光轴上距离透镜中心$f$的一个点上。对于非常薄的透镜来说，用$R_1$ 表示物体所在一侧透镜的曲率，用$R_2$表示像所在一侧透镜的曲率，用$n$表示透镜的折射率，可用下式计算该透镜的焦距：
  $$\frac{1}{f}=(n-1)(\frac{1}{R_1}-\frac{1}{R_2})$$
  此公式中，当物体所在一侧透镜是凸面时，透镜表面的曲率半径$R_1$是正数，而当像所在一侧透镜是凸面时，透镜表面的曲率半径$R_2$是负数。当然，实际的透镜都有一定的厚度，用$d$来表示透镜的厚度，可将将上述计算公式扩展为：
  $$\frac{1}{f}=(n-1)(\frac{1}{R_1}-\frac{1}{R_2})+\frac{d(n-1{)}^2}{n{R}_1{R}_2}$$
  可以看出，对于两侧都是凸面的透镜来说，透镜越厚，焦距越长，另外可以直接计算两个非常薄的透镜所组成的透镜组的组合焦距，用$f_1$表示第一个透镜的焦距，用$f_2$表示第二个透镜的焦距，用$a$表示两个透镜的间距，则组合焦距可以做如下表示：
  $$\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}-\frac{1}{f_1{f}_2}$$

  
  
  单透镜成像示意图

• 屈光度(Diopter):一个光学系统的屈光度就等于以米为单位的焦距的导数：$\varphi =\frac{1}{f}$

• 透镜焦度(Refractive Power): 焦距的倒数体现了透镜的折光能力，称为透镜焦度，一个透镜的焦度大程度上意味着透镜的折射能力强。

• 孔径光阑(Aperture Stop): 限制成像光束立体角，决定了轴上点成像光束中最边缘光线的倾斜角(F-stop对应相机光圈测量值，F对应镜头焦距，stop对应镜头的数值孔径，F-stop越小光圈越大)

  
  
  孔径光阑

• 视场光阑(Field Diaphragm):限制物空间能被系统成像的最大范围，决定了光学系统的视场

  
  
  孔径光阑与视场光阑

• 渐晕光阑(Vignetting Stop):使物空间轴外发出的光线只能部分通过，目的是减小轴外像差

• 消杂光光阑:对从视场外入射系统的光能和由镜头内部的光学表面、金属表面、镜头内壁的反射和散射所产生的杂散光起限制作用。

• 放大率(Magnification):像的大小与物的大小的比率

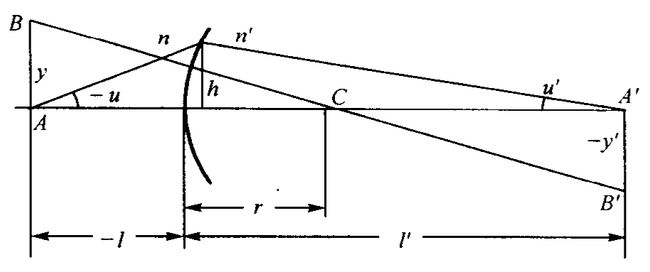
  • 横向放大率: 垂直光轴的物体成像时，像的大小与物的大小之比：$\beta =\frac{y^{\prime }}{y}=\frac{l^{\prime }-r}{l-r}=\frac{n{l}^{\prime }}{n^{\prime }l}$
  • 轴向放大率: 像点与对应物点沿光轴移动量之比：$\alpha =\frac{d{l}^{\prime }}{dl}=\frac{n{l}^{\prime 2}}{d{l}^{\prime 2}}=\frac{n^{\prime }}{n}\beta$
  • 角放大率: 折射前后的一对光线与光轴夹角之间的比值：$\gamma =\frac{u^{\prime }}{u}=\frac{l}{l^{\prime }}=\frac{n}{n^{\prime }\beta }$

垂直光轴物体AB被球面成像的情况

• F-Number: 聚焦光束张角的一半${\theta }^{\prime }$为自变量的镜头参数：$F=\frac{1}{2sin{\theta }^{\prime }}$​

  由于与光束的横截面积相关，镜头的亮度(像平面的亮度)与$F$数的平方成反比，这意味着$F$数越大，通过镜头的光亮越小，所成的像就越暗。但实际镜头的性能还被其表面对光的反射和内部光学材料对光线的吸收所影响，所以镜头的亮度不能只用$F$数来表示，很多场合下亮度还可以用$T$数来表示，$T$数与$F$数相当，只是额外考虑了成像光学器件的透明度(T)。为了提高成像光学器件的透明度，必须抑制光学系统元件表面的反射现象。无论如何，本质上可以认为亮度与有效$F$数的平方成反比，与光学系统的透明度(T)成正比。用$E_0$表示物体的亮度(照度)，则像平面的亮度$E_i$可以表示作如下表示：
  $$E_i=\frac{\pi }{4}{E}_{0}T(\frac{1}{(1+\beta )F}{)}^2$$
  以上为像中心的亮度，像边缘的亮度一般要比这个值低，即边缘衰减效应。

• 等效透镜(Equivalent Lens): 下图中的第一个透镜是凹透镜，第二个透镜是凸透镜，整体作用等效于只在位置$A$处放置一个透镜，因此，整个透镜组长度相对于其焦距而言很长，称为逆望远型镜头，经常被应用在广角镜头和紧凑型数码变焦镜头中。

逆望远型镜头示意图

下图中的第一个透镜是凸透镜，第二个镜头是凹透镜，整体作用等效于只在位置$B$处放置一个透镜，这种组合结构使得整个透镜组的长度可能短于焦距，称为望远型镜头，被广泛应用在长焦镜头和紧凑型胶片机的变焦镜头中。

望远型镜头示意图

几何像差

绝大多数实际光学系统的成像是不完善的，像差就是不完善之处的具体表述，几何像差是最直观、最容易同光学系统结构参数建立联系的表述方法。镜头的理想成像，简单来说，应当满足以下几个条件：

①点所成像仍为点

②平面所成像仍为平面

③物体和它的成像形状一样

镜头不能满足这些条件的原因在于其中存在像差。只有平面反射镜是唯一能对物体成完善像的光学器件，单个球面镜或任意组合的光学系统，只能对近轴物点以细光束成完善像，随着视场合孔径的增大，成像光束的同心性遭到破坏，产生各种成像缺陷，使像的形状与物不再相似，这些成像缺陷可用若干种像差来描述。如果只考虑单色光成像，光学系统可能产生五中性质不同的像差，即球差、慧差、像散、相面弯曲、畸变，统称为单色像差。但是，绝大多数光学系统用白光或者复合光成像，由于色散的存在会使得其中不同的色光有不同的传播光路，由于这种光路差别而引起的像差称为色像差，包括位置色差和倍率色差。

球差(Spherical Aberration)

球差是轴上点单色像差，是所有几何像差中最简单也是最基本的像差，形成球差的根本原因是镜头的中心区域和边缘区域对光线的汇聚能力的不同，光轴上一点发出的同心光束经光学系统各个球面折射后，将不复为同心光束，与光束不同夹角的光线交光轴于不同位置，相对于理想像点的位置有不同程度的偏离，称为球差。

球差示意图

球差剖面图

球差截面图(从上至下分别表示无球差校正、适当球差校正、过球差校正；从左至右分别表示从像距小于焦距、等于焦距、大于焦距)

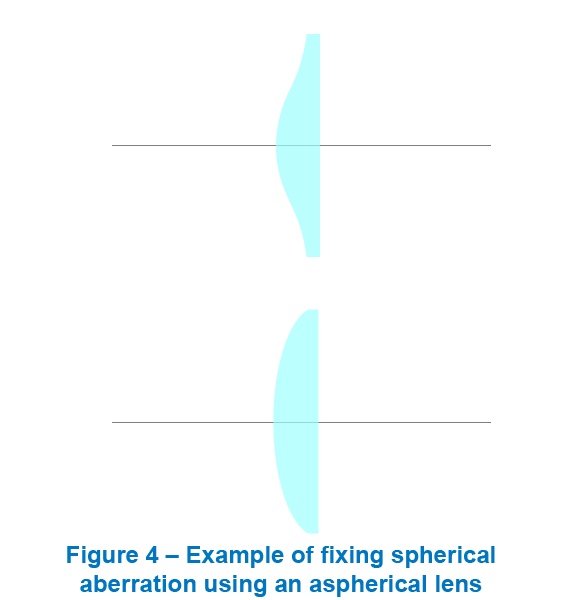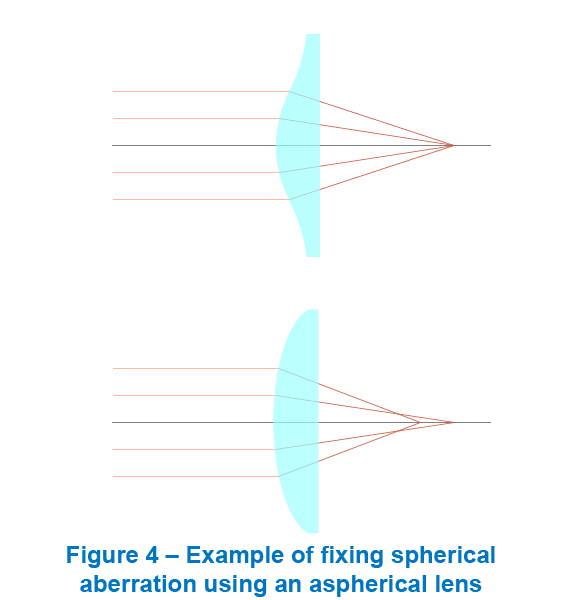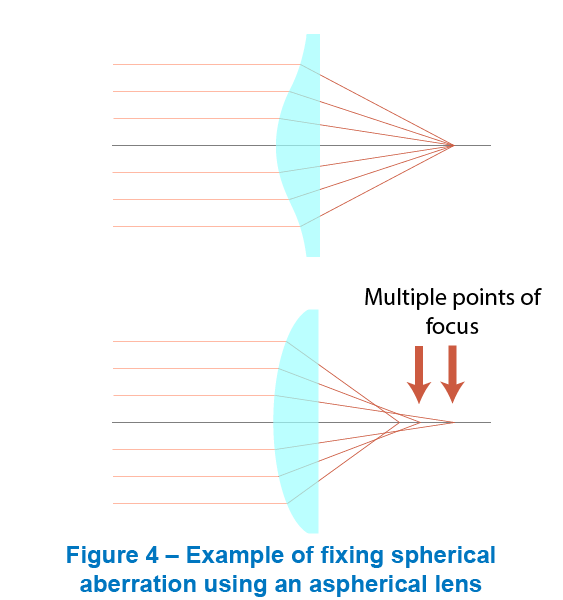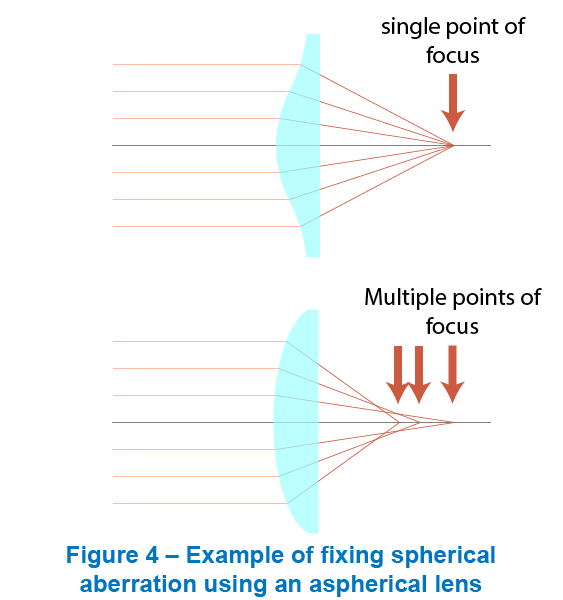
可以看出，距离光轴越远的入射光线，形成的球差越大，因此可以通过适当减小光圈尺寸来降低球差，此外还可以通过使用更复杂的非球面透镜来最小化球面像差。

两种简单的球差校正示意图

球差对成像质量的危害，是在理想像平面上引入了一定尺寸的弥散圆，造成了图像的模糊。

球差将造成图像模糊

如上图<球差示意图>所示，透镜表面的光离光轴越远，所产生的球差越大，可以通过减小通过孔径来降低的镜头的球差，进而改善成像质量，但随着通过空间的减小，由衍射所产生的艾里斑直径将扩大，也会造成图像的模糊，因此通过降低通过孔径带来的成像质量的改善程度有限。

慧差(Coma)

慧差是一种描述轴外点光束关于主光线失对称的像差，是轴外点成像时产生的一种宽光束像差，与视场和孔径均有关系，对于单个球面，慧差一方面由球差引起，球差越大，慧差也越大，另一方面，慧差是轴外点成像时产生的一种宽光束像差，与视场角和孔径相关。孔径越大，像空间中由慧差形成的彗星状的弥散斑也越大。

慧差形成示意图

光阑孔径大小对慧差的影响

慧差对成像质量的影响

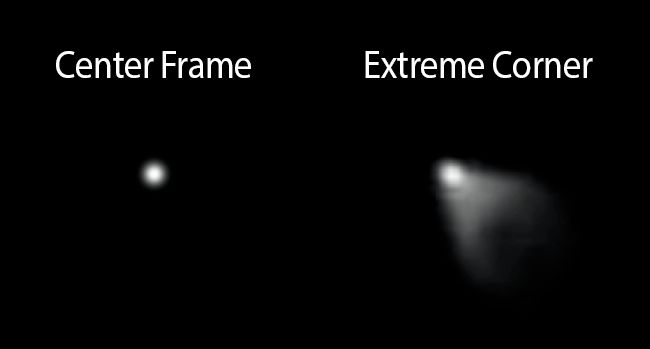
慧差主要破坏轴外视场成像的清晰度，越靠近图像边缘慧差越明显，大视场的光学系统必须校正慧差。

像散(Astigmatism)

像散是点光源被投影成线或椭圆导致的像差，与慧差是比较接近的，但是对光圈孔径大小不敏感，更加依赖于光束的斜角，像差表现为样本点的离轴图像显示为线或椭圆，根据进入透镜的离轴光线的角度，像散图像可以在两个不同方向中的任意一个方向成扩散的弥散斑，受焦点的影响，线的形状像是旋转了90度，例如，垂直线变成了水平线。

像散示意图

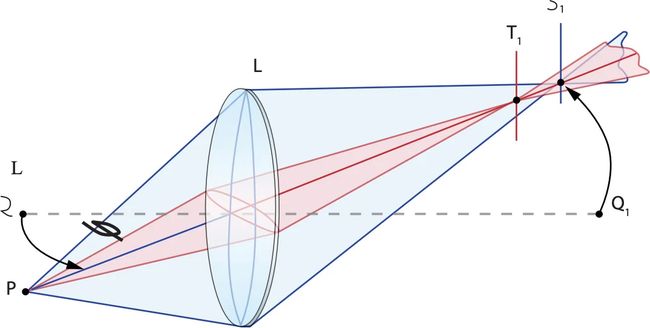
如上图所示的子午光束(蓝色)和弧矢光束(红色)汇聚点之间的位置差异使得成像表现出失对称性，即是像散。

非对称细光束的聚焦情况：下方为成像所成的弥散斑

像散对成像质量的影响

有无像散的成像示意图(上：无像散，下：有像散)

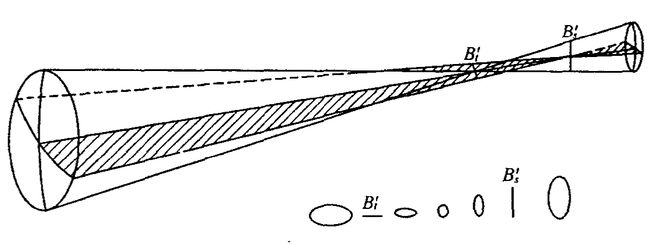
随着视场的增大，像散迅速增大，越靠近图像边缘像散越明显，可以通过收缩光圈进行缓解。

场曲(Field Curvature)

场曲也称Petzval field curvature，当物体是一个平面时，这种像差会导致焦平面是相切于高斯像面中心点的曲面，即像面弯曲，这是由于光学元件的弯曲特性，透镜以曲面的方式而不是平面的方式投射图像，或者说场曲是指透镜没有将光线完美聚焦在一个平面上，而是聚焦在一个假想的曲面上。但和前面几种像差不同的是，场曲不形成或增大弥散斑，不会从根本上模糊图像，如果像素阵列保持和像面相同的弯曲程度，就能对场景成清晰的像，但是，目前大多数相机的传感器都是平面的，这将会导致像仅在特定部分清晰，而不是整个画面上均匀清晰，可以在镜头设计中加入凹面镜进行更正，但这回使得镜头整体变长，并且加入的凹面镜需要靠近像平面来减少镜头的后焦距。常见的场曲有球面场曲和波面场曲，其对应的图像模糊区域的分布特征有所区别。

波面场曲和球面场曲示意图

场曲对图像质量的影响

由于场曲随着视场的增加而增加，因此减小光圈大小可以降低场曲，另一种方式是在靠近像面的一侧添加一个具有相反场曲的透镜，用以抵消前面透镜存在的场曲。

畸变(Distortion)

对于理想光学系统，一对共轭平面上的放大率是常数，但对于实际光学系统，只当视场较小时具有这一性质，当视场较大时，像的放大率随视场而异，这样就会使像相对于物体失去相似性，这种使像变形的像差为畸变。

畸变产生原因示意图

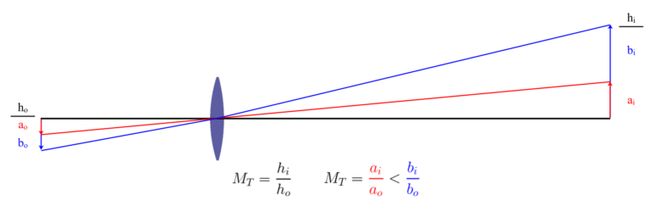
可以看出，畸变主要是由轴外像点的放大率与轴上像点的放大率间的差异造成的，如下图所示，C CC表示无畸变的高斯像面，越靠近镜头边缘时，当放大率大于高斯像面的放大率时，为正畸变，呈枕型；当放大率小于高斯像面的放大率时，为负畸变，呈桶型。此外还有胡型畸变，是枕型畸变和桶型畸变的组合。另外，和场曲相似的是，畸变并不从影响透镜成像的清晰度，本身不会对MTF产生影响，并且畸变不能通过减小光圈尺寸来校正。

枕型畸变、桶型畸变与高斯像面的比较

枕型畸变、桶型畸变、胡型畸变示意图

畸变对图像质量的影响

轴向色差(Longitudinal/Axial Chromatic Aberration)

透镜对于不同的波长的光有不同的焦点，造成不同色光对轴上物点成像位置差异。口径越大的镜头越容易产生这种色差，一般可以通过缩小光圈来减弱轴向色差。

轴向色差示意图

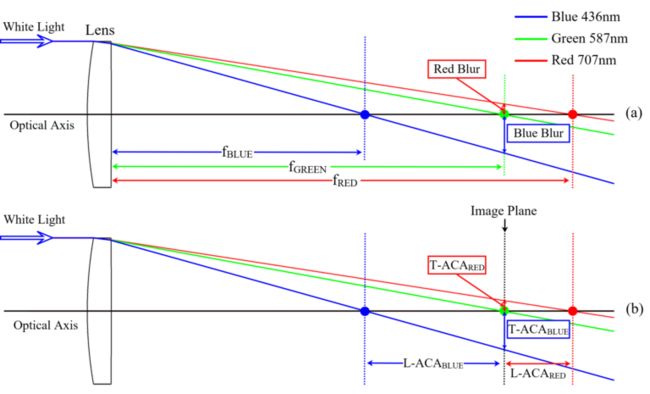
而人眼对于G通道更敏感，不管是Bayer域还是YUV域的自动对焦统计信息，G通道的统计信息的影响都更大，一般认为G通道可以正确对焦，从而引起R、B的模糊，造成高光区与底光区交界处出现明显的紫边现象(Purple Fringing)，靠近中心偏红，远离中心偏蓝。

轴向色差产生伪色

横向色差(Lateral Chromatic Aberration)

轴外白光经透镜折射后，不同波长的像高不同，即不同波长的光会聚焦在焦平面上不同的位置，造成R、G、B通道具有不同的像高，产生颜色的错位，当横向色差严重时，会使物体的像带有彩色的边缘。于是，从像的中心看去可以看到点对称的颜色扩散，这种色差并不能通过减小光圈尺寸进行校正，需要通过标定R、B通道相对于G通道的倍率偏移量，对R、B通道进行相应的缩放来实现校正。

横向色差示意图

横向色差产生色彩边缘

衍射的影响(Diffraction)

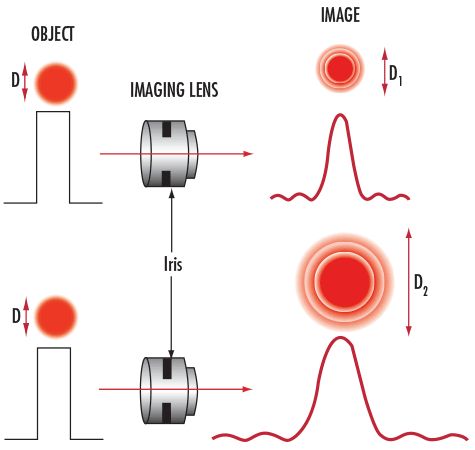
光有波动性，对于传统的胶片机中的光学成像器件，其设计仅考虑光的折射和反射，但对于拥有很小像素间距的数码相机而言，必须考虑衍射问题，衍射涉及光线在物体周围弯曲的方式。

在将光简单看做直线的几何方法中，点状物体用无像差镜头所成的像可以被聚焦成一个点，然而，在波动光学中需要考虑波动性，点状物体所成的像不再聚焦成一个点。例如，给一个圆形小孔和无像差镜头，就能形成一个被一系列暗的同心圆所包围的亮斑，即是艾里斑，而且第一级圆环(一级衍射光)的亮度只有中心亮度的1.75%，虽然它很暗，但的确存在，艾里斑是限制镜头分辨率的主要原因。

艾里斑示意图

第一个暗环的半径$r$由下式给出：
$$r=1.22\lambda F$$
其中$\lambda$为波长，$F$为F-Number，1.22由第一类贝塞尔函数导出。

圆孔半径对衍射的影响

艾里斑随通过孔径的减小而增大

F数对艾里斑半径的影响示意图

F/#	波长为520nm时的艾里斑直径(um)
1.4	1.78
2	2.54
2.8	3.55
4	5.08
5.6	7.11
8	10.15
11	13.96
16	20.30

瑞利将两个点光源图像之间第一暗环之间的距离作为对两个点光源图像分辨能力的标准，就是瑞利极限，和空间频率的倒数相关，这种关系可表示为：
$$MTF(v)=\frac{2}{\pi }cos{(}^{-1}(\lambda Fv))-\lambda Fv\sqrt{1-(\lambda Fv{)}^2}$$
其中$v$为空间频率，下图为具有圆形光圈的理想镜头的F数与氦的$d$线(587.56nm)单色光的MTF频率特征的关系图。

F数与MTF关系图

Summary

光学系统中的像差直接影响成像质量，最终影响机器视觉系统的整体性能，镜头主要参数对成像质量的影响：

• 焦距越小，景深越大，畸变越大，shading越严重
• 光圈越大，图像越亮，景深越小，分辨率越高(艾里斑越小)，球差和慧差越严重，shading越严重
• 越靠近图像边缘，分辨率越低，亮度越低(光场照度越低)，畸变越严重
• 在相同相机及镜头参数下，光源的波长越短，镜头的分辨率越高，所在需要进行精密测量的视觉项目中，可以尽量采用短波单色光作为照明光源，对提升视觉系统的稳定性和精度有很大帮助

如果只考虑单色光成像，光学系统可能产生五种性质不同的像差，即球差、慧差、像散、场曲、畸变，前三种会形成弥散斑，将从本质上造成成像的模糊，场曲不会形成弥散斑，但由于弯曲的虚拟像面与传感器阵列之间必然存在的不完美契合，在传感器是形成弥散斑，从而造成成像的模拟，畸变始终不造成成像的模糊，只使图像产生扭曲。因此，前4中都会影响镜头的空间分辨率MTF，畸变不对MTF产生影响。

任何光学介质，对透明波段中不同波长的单色光具有不同 折射率，波长短者折射率大。光学系统多半用白光成像，白光入射于任意形状的介质分界面时，只要入射角不为零，各种色光将因色散而有不同的传播途径，结果导致各种色光有不同的成像位置和不同的成像倍率，形成成像的色差，其中影响轴上物点成像位置差异的色差为轴向色差，影响轴外物体成像倍率的色差Wie横向色差。可以看出，色差会形成弥散斑，将从本质上造成成像的模糊，从而对MTF产生影响。另外，球差、轴向色差均是轴上色差，像散、场曲、畸变、横向色差均是轴外像差。

Reference

1. Aperture and Field Stops

2. 渐晕原理

3. 望远镜中像差产生过程的几何原理

4. 像差像素过程的动画演示

5. 镜头像差总结

6. 一些镜头成像的常见现象示意

7. 《Geometric Optics, Aberrations and Optical Design》

8. 《Image Sensors and Signal Processing For Digital Still Cameras》

9. 《几何光学.像差.光学设计》