Atcoder Beginner Contest 305——D-F题讲解

蒟蒻来讲题，还望大家喜。若哪有问题，大家尽可提！

Hello, 大家好哇！本初中生蒟蒻讲解一下AtCoder Beginner Contest 305这场比赛的D-F题！

===========================================================================================

D题

题外话

安利一波自己的洛谷博客：点这里

思路

这道题还是比较简单的~~~
首先探讨一下什么时候会睡觉：当 $A_i-A_j$ 时，i 为奇数，j 为偶数时，他会睡觉！

主要分一下三步：

1. 我们用一个前缀和记录从时间点 $0$ 到 $A$ 数组中的每一个时间点的睡觉时间。

2. 对于每一个询问的区间 $l_i,r_i$，我们通过 lower_bound 函数找到在数组 $A$ 中的位置，记作 $pa,pb$。

3. 首先睡觉的时间定为 $slee{p}_{pb}-slee{p}_{pa-1}$。

   ①若 $pb$ 是奇数，即询问的区间的右端点 $r_i$ 正好在睡觉区域内，那么我们就将睡觉的时间减去从 $r_i$ 到 $A_{pb}$ 的时间。

   ②若 $pa$ 是奇数，即询问的区间的左端点 $l_i$ 正好在睡觉区域内，那么我们就将睡觉的时间减去从 $A_{pa-1}$ 到 $l_i$ 的时间。

我们看张图理解一下：

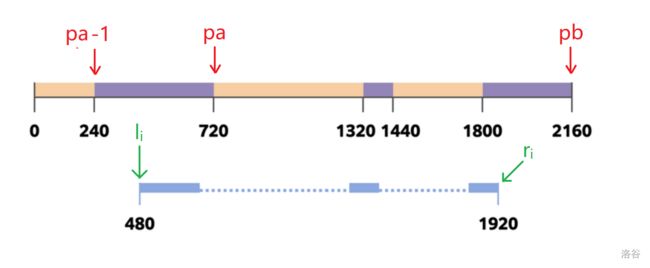
这张图就是我们所定义出来的点的位置。
若我们将记录从时间点 $0$ 到 $A$ 数组中的每一个时间点的睡觉时间的前缀和数组记作 $sleep$。

那么，我们的答案就是 $slee{p}_{pb}-slee{p}_{pa-1}-(l_i-A_{pa-1})-(A_{pb}-r_i)$。

如果是这样，那么就不能减右边的了，所以是 $slee{p}_{pb}-slee{p}_{pa-1}-(l_i-A_{pa-1})$。

代码

#include 

using namespace std;

const int N = 2e5 + 10;

int n;
int a[N], sleep[N];
int q;
int l, r;

int main()
{
	cin >> n;
	
	for (int i = 1; i <= n; i ++)
		cin >> a[i], sleep[i] = sleep[i - 1] + (a[i] - a[i - 1]) * (i & 1); //计算前缀和
		
	cin >> q;
	while (q --)
	{
		cin >> l >> r;
		 
                //计算睡觉时间
		int pa = lower_bound(a + 1, a + 1 + n, l) - a;
		int pb = lower_bound(a + 1, a + 1 + n, r) - a;
		
		int minus = 0;
		if (pa & 1) minus += a[pr] - r;
		if (pb & 1) minus += l - a[pl - 1];
		
		cout << sleep[pr] - sleep[pl - 1] - minus << endl;
	}
}

---

E题

题外话

安利一波自己的博客：点这里

思路

这道题我们转化一下题意：

对于每一个守卫，我们找到哪些点与他的距离小于等于他的耐力。

这样，我们就会好做许多！

这时，我们就可以利用 多源BFS 的思路，将所有的节点入队，之后我们对于每一个节点存一下他的耐力，然后向四周扩展，每次扩展一次让扩展到的点的耐力都减一，直到所有点的耐力都为0为止，对于所有遍历到的点，都是答案。

这样，我们需要一个 priority_queue 来将耐力从大到小排，保证我们最后会让所有点的耐力为 $0$

代码

#include 
#include 
#include 
#include 
#include 

using namespace std;

const int N = 2e5 + 10;
typedef pair<int, int> PII;

int n, m, k;
int a, b;
int p, h;
vector<int> g[N];
int st[N];
vector<PII> guard;

void bfs()
{
	priority_queue<PII, vector<PII>, less<PII>> heap;
	
	for (int i = 1; i <= k; i ++) //多源BFS：将所有点入队，注意要让耐力为参数1，因为C++自动按参数1排序
		heap.push({guard[i].second, guard[i].first});
		
	while (heap.size()) //BFS
	{
		auto t = heap.top();
		heap.pop();
		
		int u = t.second, left = t.first;
		
		if (left == -1) break; //说明所有点的耐力为0了，就可以停止了
		if (st[u]) continue;
		st[u] = 1;
		
		for (auto c : g[u])
			heap.push({left - 1, c}); //此时，因为扩展了一步，耐力-1
	}
}

int main()
{
	cout.tie(0);
	cin.tie(0);
	ios::sync_with_stdio(0);
	
	cin >> n >> m >> k;
	
	while (m --)
	{
		cin >> a >> b;
		g[a].push_back(b);
		g[b].push_back(a);
	}
	
	guard.resize(k + 1);
	for (int i = 1; i <= k; i ++)
		cin >> p >> h, guard[i] = {p, h};
		
	bfs();
	
	vector<int> ans;
	for (int i = 1; i <= n; i ++)
		if (st[i])
			ans.push_back(i);
			
	cout << ans.size() << endl;
	for (auto c : ans)
		cout << c << " ";
	
	return 0;
}

---

F题

题外话

安利一波自己的博客：点这里

思路

这是一道罕见的交互题，其实感觉没E题难

这道题就是我们不停地走，然后记录一下走了哪些点，不要走重复的点。如果走着走着走不动了，也就是剩下的点都是走过的点，我们就再往回走，走上一个点的另一种走法。

这样走最坏情况下，会走 $2N-1$ 步，因为假设我们除了终点和起点的点全走空了，都会回到最初起点 $1$，这样就走了 $2N-2$ 步，最后我们一步到达终点，就是 $2N-1$ 步了。

代码

#include 
#include  

using namespace std;

const int N = 1e2 + 10;

int st[N];

int main()
{
	cout.tie(0);
	cin.tie(0);
	ios::sync_with_stdio(0);
	
	int n, m;
	
	cin >> n >> m;
	
	int pl = 1;
	vector<int> pass; //记录走的路程
	pass.push_back(1);
	while (pl != n)
	{
		int k, p;
		
		cin >> k;
		
		st[pl] = 1; //记录走了的点
		vector<int> to;
		for (int i = 1; i <= k; i ++)
			cin >> p, to.push_back(p);
			
		int flg = 0;
		for (auto c : to) //找到以个没走过的点走
			if (!st[c])
			{
				pl = c;
				cout << pl << endl;
				pass.push_back(c);
				flg = 1;
				break;
			}
		
		if (!flg) //得往回走了！
		{
			pass.pop_back();
			pl = pass.back();
			cout << pl << endl;
		}
	}
	
	string s;
	
	cin >> s;
	
	return 0;
}

---

大家有什么问题尽管提，我都会尽力回答的！

吾欲您伸手，点的小赞赞。吾欲您喜欢，点得小关注！