频谱细化-----Zoom-FFT算法介绍及MATLAB实现
栅栏效应
若长度为 N = T / d t = T ⋅ f s N=T/dt=T\cdot {{f}_{s}} N=T/dt=T⋅fs,其中 T T T为采样时间, d t dt dt为采样间隔, f s f_s fs为采样频率,通过傅里叶变换后得到 X ( f i ) X\left( {{f}_{i}} \right) X(fi), f i = i ⋅ f s / N , i = 0 , 1 , 2 , . . . , N / 2 {{f}_{i}}=i\cdot {{f}_{s}}/N,i=0,1,2,...,N/2 fi=i⋅fs/N,i=0,1,2,...,N/2,由于频率分辨率的限制,那么相邻两个离散点之间的频率无法获得,会导致部分有用的频率被漏掉,这就是所谓的栅栏效应。
解决这种问题的一种方法是可以增加数据的点数或者提高傅里叶变换的点数,但是这样会增加系统的硬件成本。不过可以通过某些方法在不改变硬件的基础上提高频率的分辨率,下面简单介绍一种经典的方法Zoom-FFT算法。
原理介绍
在实际的应用中,只需要对感兴趣的某段频率的信号进行分析,下面介绍一种基于复调制的频谱细化方法。

复调制移频
模拟信号 x ( t ) x\left( t \right) x(t)经过A/D变换后转化为离散信号 x 0 ( n ) {{x}_{0}}\left( n \right) x0(n)。如果感兴趣的频带为 f 1 ∼ f 2 {{f}_{1}}\sim {{f}_{2}} f1∼f2,中心频率为 f e = ( f 1 + f 2 ) / 2 {{f}_{e}}=\left( {{f}_{1}}+{{f}_{2}} \right)/2 fe=(f1+f2)/2,对 x 0 ( n ) {{x}_{0}}\left( n \right) x0(n)进行复调制,可以得到
x ( n ) = x 0 ( n ) e − j 2 π n f e / f s = x 0 ( n ) cos ( 2 π n f e / f s ) − j x 0 ( n ) sin ( 2 π n f e / f s ) = x 0 ( n ) cos ( 2 π n L 0 Δ f / N Δ f ) − j x 0 ( n ) sin ( 2 π n L 0 Δ f / N Δ f ) = x 0 ( n ) cos ( 2 π n L 0 / N ) − j x 0 ( n ) sin ( 2 π n L 0 / N ) \begin{aligned} & x\left( n \right)={{x}_{0}}\left( n \right){{e}^{-j2\pi n{{f}_{e}}/{{f}_{s}}}}={{x}_{0}}\left( n \right)\cos \left( 2\pi n{{f}_{e}}/{{f}_{s}} \right)-j{{x}_{0}}\left( n \right)\sin \left( 2\pi n{{f}_{e}}/{{f}_{s}} \right) \\ & ={{x}_{0}}\left( n \right)\cos \left( 2\pi n{{L}_{0}}\Delta f/N\Delta f \right)-j{{x}_{0}}\left( n \right)\sin \left( 2\pi n{{L}_{0}}\Delta f/N\Delta f \right) \\ & ={{x}_{0}}\left( n \right)\cos \left( 2\pi n{{L}_{0}}/N \right)-j{{x}_{0}}\left( n \right)\sin \left( 2\pi n{{L}_{0}}/N \right) \\ \end{aligned} x(n)=x0(n)e−j2πnfe/fs=x0(n)cos(2πnfe/fs)−jx0(n)sin(2πnfe/fs)=x0(n)cos(2πnL0Δf/NΔf)−jx0(n)sin(2πnL0Δf/NΔf)=x0(n)cos(2πnL0/N)−jx0(n)sin(2πnL0/N)
其中, f s = N Δ f {{f}_{s}}=N\Delta f fs=NΔf是采样频率, Δ f \Delta f Δf是谱线间隔, L 0 = f e / Δ f {{L}_{0}}={{f}_{e}}/\Delta f L0=fe/Δf为频率的中心移位,频谱显示对应中心频率的谱序号,即 f e = L 0 Δ f {{f}_{e}}={{L}_{0}}\Delta f fe=L0Δf。同时可以看出,复调制使得 x 0 ( n ) {{x}_{0}}\left( n \right) x0(n)的 f e {{f}_{e}} fe搬移到 x ( n ) x\left( n \right) x(n)的零频点,即 X 0 ( k ) {{X}_{0}}\left( k \right) X0(k)的第 L 0 {{L}_{0}} L0条谱线移到 X ( k ) X\left( k \right) X(k)中零点频谱的位置.为了得到 X ( k ) X\left( k \right) X(k)零点附近的部分细化频谱,可重新抽样把频率降到 f s / D {{f}_{s}}/D fs/D, D D D为细化倍数。为了使得抽样后的频率不发生频谱混叠,需要在抽样前进行低通滤波。
低通滤波
为了保证重新采样后的信号在频谱分析时不发生频谱混叠,需进行抗混叠滤波,滤出需要分析的频段信号,则数字低通滤波器的截止频率 f c ≤ f s / 2 D {{f}_{c}}\le {{f}_{s}}/2D fc≤fs/2D
重新抽样
信号经过移频、低通滤波后,分析信号点数变少,再以较低的采样频率进行重新采样,在通过补零保证相同的采样点数时,样本的总长度加大,频谱的分辨率也就得到了提高。
设原采样频率为 ,采样点数为 N N N,则频率分辨率为 f s / N {{f}_{s}}/N fs/N,现重采样频率为 f s / D {{f}_{s}}/D fs/D,当采样点数仍是 N N N时,其分辨率为 f s / ( D ∗ N ) {{f}_{s}}/\left( D*N \right) fs/(D∗N),分辨率提高了 D D D倍。这样就在原采样频率不变的情况下得到了更高的频率分辨率。
复数FFT
重新采样后的信号实部和虚部是分开的,需要对信号进行N点复FFT,从而得出 N N N条谱线,此时分辨率为 Δ f ′ = f s ′ / N = f s / N D = Δ f / D \Delta {{f}^{'}}=f{{{}_{s}}^{'}}/N={{f}_{s}}/ND=\Delta f/D Δf′=fs′/N=fs/ND=Δf/D,可见分辨率提高了 D D D倍。
频率调整
经过算法运行后的谱线不为实际频率的谱线,需要将其反向搬移,转换成实际频率,进而得出细化后的频率。
下面对该方法进行仿真,仿真参数如下
| 参数值 | 参数名称 |
|---|---|
| 采样频率 | 1000Hz |
| 细化倍数 | 50 |
| 滤波器阶数 | 200 |
| FFT点数 | 2048 |
| 频率 | 166.4Hz、165Hz |
结果如下
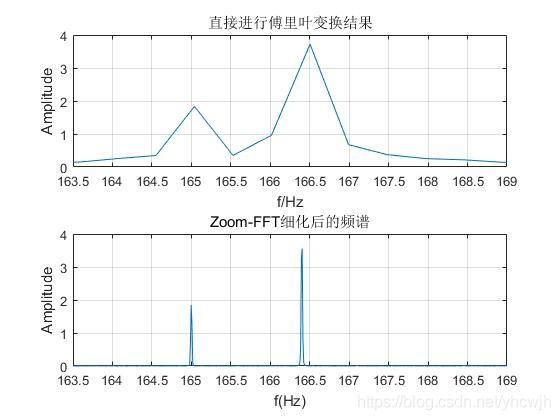
从图中可以看出,直接进行FFT,频率与原始频率有些许误差,并且不是很能分辨,但是细化后的频谱能够很好地区分信号的频率,很准确地得到了信号的频率。
代码如下:
clear;
close all;
clc;
fs=1000; %采样频率
N=2048; %傅里叶变换点数
D=50; %细化倍数
M=200; %滤波器阶数
t=(0:N*D+2*M)/fs; %时间轴
x=4*sin(2*pi*166.4*t)+2*sin(2*pi*165*t+pi/6)...
+0.6*randn(1,N*D+2*M+1); %信号
xf=fft(x,N); %傅里叶变换
xf=abs(xf(1:N/2))/N*2;
subplot(211);
plot((0:N/2-1)*fs/N,xf);
axis([163.5 169 0 4])
grid on
xlabel('f/Hz');ylabel('Amplitude')
title('直接进行傅里叶变换结果')
fe=167; %中心频率
k=1:M;
w=0.5+0.5*cos(pi*k/M); %Hanning函数
fl=max(fe-fs/(4*D),-fs/2.2); %频率下限
fh=min(fe+fs/(4*D),fs/2.2); %频率上限
yf=D*fl;
df=fs/D/N; %分辨率
f=fl:df:fl+(N/2-1)*df;
xz=zeros(1,N/2);
wl=2*pi*fl/fs; %归一化角频率
wh=2*pi*fh/fs;
hr(1)=(wl-wh)/pi;
hr(2:M+1)=(sin(wl*k)-sin(wh*k))./(pi*k).*w;
hi(1)=0;
hi(2:M+1)=(cos(wl*k)-cos(wh*k))./(pi*k).*w;
p=0:N-1;
w=0.5-0.5*cos(2*pi*p/N);
xrz=zeros(1,N/2);
xiz=zeros(1,N/2);
L=10; %循环次数
for i=1:L
for k=1:N
kk=(k-1)*D+M;
xrz(k)=x(kk+1)*hr(1)+sum(hr(2:M+1).*(x(kk+2:kk+M+1)+x(kk:-1:kk-M+1)));
xiz(k)=x(kk+1)*hi(1)+sum(hi(2:M+1).*(x(kk+2:kk+M+1)-x(kk:-1:kk-M+1)));
end
xzt=(xrz+1j*xiz).*exp(-1j*2*pi*(0:N-1)*yf/fs);
xzt=xzt.*w;
xzt=xzt-sum(xzt)/N;
xzt=fft(xzt);
xz=xz+(abs(xzt(1:N/2))/N*2).^2;
end
xz=(xz./L).^0.5;
subplot(212);
plot(f,xz);
axis([163.5 169 0 4])
grid on
xlabel('f(Hz)');ylabel('Amplitude')
title('Zoom-FFT细化后的频谱')
参考文献:
[1]王旭刚. 基于FMCW体制K波段测距雷达的研究与实现[D].南京航空航天大学,2012.