数据结构与算法——动态规划（DP）

1. 应用场景

求解最优解的值，而非搞清楚如何构造的最优解

举例说明：

• 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。求有多少种不同的方法可以爬到楼顶。
• 你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，你不能偷窃两间相邻的房屋，求一夜之内能够偷窃到的最高金额。
• 给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。求出该最小路径和。

2. DP状态

「DP 状态」的确定主要有两大原则：最优子结构、无后效性

2.1 最优子结构

如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理

将原有问题化分为一个个子问题，即为子结构。而对于每一个子问题，其最优值均由【更小规模的子问题的最优值】推导而来，即为最优子结构。因此 DP 状态设置之前，需要将原有问题划分为一个个子问题，且需要确保子问题的最优值由更小规模子问题的最优值推出，此时子问题的最优值即为【DP 状态】的定义。

例如在爬楼梯例题中，原有问题是【到第n层台阶的方法数】，子问题是【到第i层台阶的方法数】。并且【到第i层台阶的方法数】由【到第i-1层台阶的方法数】和【到第i-2层台阶的方法数】推出，此时后者即为更小规模的子问题，因此满足【最优子结构】原则。由此我们才定义【DP 状态】表示子问题的最优值，即【到第i层台阶的方法数】。

2.2 无后效性

即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关

• 【无后效性】：我们不关心【DP 状态】中是如何推出【到第i-1层台阶的方法数】和【到第i-2层台阶的方法数】，即不关心这个子问题的最优值是从哪个其它子问题转移而来，说明了【无后效性】。

• 【有后效性】：假设不能连续跨2层台阶，即我们需要关心【到第i-2层台阶的方法数】中有哪些是包含了跨2层台阶上到【到第i-2层】的

2.3 解题思路

贪心求解局部最优，局部最优不一定全局最优
DP求解全局最优，全局最优一定包含某些时刻的局部最优

• 刻画一个最优解的结构特征：【DP状态】
• 递归定义最优解的值：【DP状态转移方程】
• 自底向上（通常）计算最优解的值：【从特殊：初始状态开始考虑】
• （如有需要）构造最优解

斐波那契数列
自底向上： `dp[0]=1,dp[1]=1,dp[2]=dp[0]+dp[1]=2,dp[3]=dp[1]+dp[2]=3,dp[4]=dp[2]+dp[3]=5`
自顶向下： `dp[n]=dp[n-1]+dp[n-2],dp[n-1]=dp[n-2]+dp[n-3],dp[n-2]=dp[n-3]+dp[n-4],直到dp[2]=d[1]+dp[1]`

3. 问题类别

3.1 线性DP

3.1.1 经典问题

3.1.1.1 LeetCode 300. 最长上升子序列

题目：

给定一个无序的整数数组，找到其中最长上升子序列的长度。

示例1：

输入: [10,9,2,5,3,7,101,18]
输出: 4 
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

思路：

如果长度为1，答案为1
如果长度为2，判断第二个数是否大于第一个数，如果大于，长度为2，否则为1
如果长度为3，依此判断第三个数、第二个数是否大于前一个数

【DP状态】：dp[i] 表示到第i个数的最长上升子序列的长度
【DP状态转移方程】：dp[i] = max(dp[j])+1，其中j < i 并且nums[j] < nums[i]

代码：

class Solution {
    public int lengthOfLIS(int[] nums) {
        if(nums.length == 0) return 0;
        int[] dp = new int[nums.length];
        int res = 0;
        Arrays.fill(dp, 1);
        for(int i = 0; i < nums.length; i++) {
            for(int j = 0; j < i; j++) {
                if(nums[j] < nums[i]) dp[i] = Math.max(dp[i], dp[j] + 1);
            }
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

3.1.1.2 LeetCode 1143. 最长公共子序列

题目：

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。

若这两个字符串没有公共子序列，则返回 0。

示例1：

输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace"，它的长度为 3。

思路：

text1[0]==text2[0] 最长公共子序列=1
text1[1]!=text2[1] 怎么办？制表法！

	text1：i	0	1	2	3	4	5
text2：j		“”	a	b	c	d	e
0	“”
1	a		1	1	1	1	1
2	c		1	1	2	2	2
3	e		1	1	2	2	3

代码：

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int m = text1.length(), n = text2.length();
        int[][] dp = new int[m + 1][n + 1];

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                // 获取两个串字符
                char c1 = text1.charAt(i), c2 = text2.charAt(j);
                if (c1 == c2) {
                    // 去找它们前面各退一格的值加1即可
                    dp[i + 1][j + 1] = dp[i][j] + 1;
                } else {
                    //要么是text1往前退一格，要么是text2往前退一格，两个的最大值
                    dp[i + 1][j + 1] = Math.max(dp[i + 1][j], dp[i][j + 1]);
                }
            }
        }
        return dp[m][n];
    }
}

3.1.1.3 LeetCode 120. 三角形最小路径和

题目：

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。

示例：

例如，给定三角形：List<List<Integer>> triangle
[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

思路：

如果自顶向下，顶层2不知道选3还是选4
所以自底向上
对第4层，向下最小路径和为1
对第3层
	6的向下最小路径和是6+min(4的向下最小路径和,1的向下最小路径和) == 6会选1
	5的向下最小路径和是5+min(1的向下最小路径和,8的向下最小路径和) == 5会选1
	7的向下最小路径和是7+min(8的向下最小路径和,3的向下最小路径和) == 7会选3
	向下最小路径和为6
对第2层
	3的向下最小路径和是3+min(6的向下最小路径和,5的向下最小路径和)）
	4的向下最小路径和是4+min(5的向下最小路径和,7的向下最小路径和)）
	
【DP状态】：对第i层第j个元素，向下最小路径和是min(第i+1层第j个元素向下最小路径和，第i+1层第j+1个元素向下最小路径和)+第i层第j个元素值
【DP状态转移方程】：dp[i][j] = triangle.get(i).get(j) + min( dp[i+1][j] , dp[i+1][j+1] )

代码：

class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        int n = triangle.size();
        // dp[i][j] 表示从点 (i, j) 到底边的最小路径和。
        int[][] dp = new int[n + 1][n + 1];
        // 从三角形的最后一行开始递推。
        for (int i = n - 1; i >= 0; i--) {
            for (int j = 0; j <= i; j++) {
                dp[i][j] = Math.min(dp[i + 1][j], dp[i + 1][j + 1]) + triangle.get(i).get(j);
            }
        }
        return dp[0][0];
    }
}

3.1.2 背包问题

3.1.2.1 01背包问题（每件物品只有1件）

给定 n 件物品，物品的重量为 weights[i]，物品的价值为 values[i]。现挑选物品放入背包中，假定背包能承受的最大重量为 total，问应该如何选择装入背包中的物品，使得装入背包中物品的总价值最大？

假设你是一个小偷，背着一个可装下4磅东西的背包，你可以偷窃的物品如下：

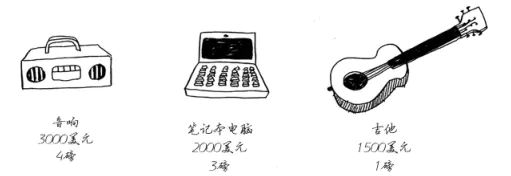
思路

• 只有1磅的背包，只能放吉他
• 只有2磅的背包，也只能放吉他
• 只有3磅的背包，吉他行填1500，音响行音响放不下，最大价值还是1500，电脑行电脑能放下，电脑价值大于吉他，填2000
• 有4磅的背包，只有吉他时只能选吉他，填1500；有吉他和音响时，放影响价值更大，填3000；有吉他音响和电脑时，可选吉他+电脑or音响，比较价值1500+2000or3000，最大能有3500价值
• weights[] = {1,3,4},values[] = {1500,2000,3000}
• 前i件物品放到容量为j的背包中获得的最大价值 = max ( 放第i件物品时 前i-1件物品放到容量为j-weights[i]的背包中获得的最大价值 , 不放第i件物品时 前i-1件物品放到容量为j的背包中获得的最大价值)
• dp[i][j] = max( values[i] + dp[i-1][j-weights[i]] , dp[i-1][j] )
• dp[ 前 i 件物品 ][ 放到容量 j 的背包 ]

背包容量/磅	1	2	3	4
吉他/1磅 1500美元	1500	1500	1500	1500
音响/4磅 3000美元	1500	1500	1500	3000
电脑/3磅 2000美元	1500	1500	2000	？

• 参考链接：https://www.cnblogs.com/kkbill/p/12081172.html

代码实现

代码实现1：多增加一行，避免判断数组越界问题

//有n件物品，他们的重量是weights，价值是values，背包最大容量是total，求能放进背包的最大价值
public int getMaxValue(int[] weights, int[] values, int total) {
	int n = weights.length;
	int[][] dp = new int[n + 1][total + 1];
	//遍历n个物品
	for (int i = 1; i <= n; i ++) {
		//遍历背包
    	for (int j = 1; j <= total; j ++) {
           	//能放下第i件物品：不放 or 放
           	if (j >= weights[i - 1]) {
           		dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weights[i - 1]] + values[i - 1]);
           	}
           	//放不下
           	else {
           		dp[i][j] = dp[i - 1][j];
           	}
       	}
	}
	return dp[n][total];
}

代码实现2：dp[i] 只与 dp[i - 1] 有关，空间压缩，从后往前遍历背包

public int getMaxValue(int[] weight, int[] value, int total) {
	int n = weight.length;
	int[] dp = new int[total + 1];
	//遍历n个物品（这里可以不用从1开始，因为dp没有i - 1的状态）
	for (int i = 1; i <= n; i ++) {
		//遍历背包：必须从后向前遍历，因为从前往后会覆盖掉前面的元素
		for (int j = total; j >= 1; j --) {
			//能放下第i件物品：不放 or 放
			if (j >= weight[i - 1]) {
				dp[j] = Math.max(dp[j], dp[j - weight[i - 1]] + value[i - 1]);
			}
			//放不下
			else {
				dp[j] = dp[j];
			}
		}
	}
	return dp[total];
}

代码实现3：优化上述代码，放不下dp的状态没变，所以可以不用考虑

public int getMaxValue(int[] weight, int[] value, int total) {
	int n = weight.length;
	int[] dp = new int[total + 1];
	//遍历n个物品
	for (int i = 0; i < n; i ++) {
		//遍历背包：必须从后向前遍历，因为从前往后会覆盖掉前面的元素
		for (int j = total; j >= weight[i]; j --) {
			//能放下第i件物品：不放 or 放
			dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);			
		}
	}
	return dp[total];
}

例题：

1. LeetCode 416. 分割等和子集

给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：

输入: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11].

填表，数组和的一半是11，即背包容量最大是11

背包容量	0	1	2	3	4	5	6	7	8	9	10	11
nums[0]:1	T	T	F	F	F	F	F	F	F	F	F	F
nums[1]:5	T	T	F	F	F	T	T	F	F	F	F	F
nums[2]:11	T	T	F	F	F	T	T	F	F	F	F	T
nums[3]:5	T	T	F	F	F	T	T	F	F	F	T	T

2. LeetCode 474. 一和零

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。	
请你找出并返回 strs 的最大子集的大小，该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。
	
示例 1：
	
输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。	

思路：把总共的 0 和 1 的个数视为背包的容量，每一个字符串视为装进背包的物品。【多维0-1背包问题】

dp[i][j][k]=min{ dp[i−1][j][k],dp[i−1][j−当前字符串使用0的个数][k−当前字符串使用1的个数]+1}

3. LeetCode 494. 目标和

给定一个非负整数数组，a1, a2, ..., an, 和一个目标数，S。现在你有两个符号 + 和 -。
对于数组中的任意一个整数，你都可以从 + 或 -中选择一个符号添加在前面。
返回可以使最终数组和为目标数 S 的所有添加符号的方法数。

示例 1：

输入：nums: [1, 1, 1, 1, 1], S: 3
输出：5
解释：

-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3

一共有5种方法让最终目标和为3。

背包容量	-5	-4	-3	-2	-1	0	1	2	3	4	5
nums[0]:1	0	0	0	0	1	0	1	0	0	0	0
nums[1]:1	0	0	0	1	0	2	0	1	0	0	0
nums[2]:1
nums[3]:1
nums[4]:1

4. 879. 盈利计划

帮派里有 G 名成员，他们可能犯下各种各样的罪行。

第 i 种犯罪会产生 profit[i] 的利润，它要求 group[i] 名成员共同参与。

让我们把这些犯罪的任何子集称为盈利计划，该计划至少产生 P 的利润。

有多少种方案可以选择？因为答案很大，所以返回它模 10^9 + 7 的值

示例1：

输入：G = 5, P = 3, group = [2,2], profit = [2,3]
输出：2
解释： 
至少产生 3 的利润，该帮派可以犯下罪 0 和罪 1 ，或仅犯下罪 1 。总的来说，有两种方案。

5. 1049. 最后一块石头的重量 II

有一堆石头，每块石头的重量都是正整数。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

如果 x == y，那么两块石头都会被完全粉碎；
如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。
最后，最多只会剩下一块石头。返回此石头最小的可能重量。如果没有石头剩下，就返回 0。

示例 1：

输入：[2,7,4,1,8,1]
输出：1
解释：
组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

将转化过程写成算式
1 - ((4 - 2) - (8 - 7))
也就是
1 + 2 + 8 - 4 - 7
换一种想法，就是：将这些数字分成两拨，使得他们的和的差最小
发散思维：求将这堆石头，放在容量为总重量一半的背包中，能放的石头的最大重量，最后的差 = 总重量 - 2 * 背包最大重量

3.1.2.2 完全背包问题（每件物品数量无限）

给定 n 类物品，每类物品的重量为 weights[i]，每类物品的价值为 values[i]，每类物品的数量可以任意选择。现挑选物品放入背包中，假定背包能承受的最大重量为 V，问应该如何选择装入背包中的物品，使得装入背包中物品的总价值最大？

思路：状态：将前 i 种物品放到限重为 j 的背包中可以获得的最大价值

状态转移：

• 不放入第 i 件物品：即将前 【i - 1】 种物品放到限重为 【 j 】的背包中可以获得的最大价值
• 放入第 i 件物品：即将前 【 i 】 种物品放到限重为 【 j - 第i件物品重量】 的背包中可以获得的最大价值（注意这里不是 i - 1，因为放下第 i 件物品还可以继续放第 i 件物品）
• weights[] = {1,3,4},values[] = {1500,2000,3000}
• dp[i][j] = max( dp[i - 1][j], values[i] + dp[i][j - weights[i]] ) 条件： weights[i] <= j

代码实现：

代码实现1：

//有n件物品，他们的重量是weights，价值是values，背包最大容量是total，求能放进背包的最大价值
public int getMaxValue(int[] weights, int[] values, int total) {
	int n = weights.length;
	int[][] dp = new int[n + 1][total + 1];
	//遍历n个物品
	for (int i = 1; i <= n; i ++) {
		//遍历背包
    	for (int j = 1; j <= total; j ++) {
           	//能放下第i件物品：不放 or 放
           	if (j >= weights[i - 1]) {
           		dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - weights[i - 1]] + values[i - 1]);
           	}
           	//放不下
           	else {
           		dp[i][j] = dp[i - 1][j];
           	}
       	}
	}
	return dp[n][total];
}

代码实现2：空间压缩：从前往后遍历背包，因为是dp[i]而不是dp[i- 1]，需要覆盖前面的元素

//有n件物品，他们的重量是weights，价值是values，背包最大容量是total，求能放进背包的最大价值
public int getMaxValue1(int[] weights, int[] values, int total) {
	int n = weights.length;
	int[] dp = new int[total + 1];
	//遍历n个物品
	for (int i = 1; i <= n; i ++) {
		//遍历背包
    	for (int j = 1; j <= total; j ++) {
           	//能放下第i件物品：不放 or 放，注意这里从前往后遍历！！！
           	if (j >= weights[i - 1]) {
           		dp[j] = Math.max(dp[j], dp[j - weights[i - 1]] + values[i - 1]);
           	}
           	//放不下
           	else {
           		dp[j] = dp[j];
           	}
       	}
	}
	return dp[total];
}
public int getMaxValue2(int[] weights, int[] values, int total) {
	int n = weights.length;
	int[] dp = new int[total + 1];
	//遍历n个物品
	for (int i = 0; i < n; i ++) {
		//遍历背包
    	for (int j = 1; j <= total; j ++) {
           	//能放下第i件物品：不放 or 放，注意这里从前往后遍历！！！
           	if (j >= weights[i]) {
           		dp[j] = Math.max(dp[j], dp[j - weights[i]] + values[i]);
           	}
           	//放不下
           	else {
           		dp[j] = dp[j];
           	}
       	}
	}
	return dp[total];
}

代码实现3：（空间压缩代码优化）

//有n件物品，他们的重量是weights，价值是values，背包最大容量是total，求能放进背包的最大价值
public int getMaxValue1(int[] weights, int[] values, int total) {
	int n = weights.length;
	int[] dp = new int[total + 1];
	//遍历n个物品
	for (int i = 1; i <= n; i ++) {
		//遍历背包
    	for (int j = weights[i - 1]; j <= total; j ++) {
           	//能放下第i件物品：不放 or 放，注意这里从前往后遍历！！！           	
           	dp[j] = Math.max(dp[j], dp[j - weights[i - 1]] + values[i - 1]);           	
       	}
	}
	return dp[total];
}
public int getMaxValue2(int[] weights, int[] values, int total) {
	int n = weights.length;
	int[] dp = new int[total + 1];
	//遍历n个物品
	for (int i = 0; i < n; i ++) {
		//遍历背包
    	for (int j = weights[i]; j <= total; j ++) {
           	//能放下第i件物品：不放 or 放，注意这里从前往后遍历！！！           	
           	dp[j] = Math.max(dp[j], dp[j - weights[i]] + values[i]);           	
       	}
	}
	return dp[total];
}

例题：

• 322. 零钱兑换
• 518. 零钱兑换 II
• 1449. 数位成本和为目标值的最大数字

3.1.2.3 多重背包问题（每件物品数量有限）

给定 n 类物品，每类物品的重量为 weights[i]，每类物品的价值为 values[i]，每类物品的数量为sizes[i]。现挑选物品放入背包中，假定背包能承受的最大重量为 V，问应该如何选择装入背包中的物品，使得装入背包中物品的总价值最大？

• weights[] = {1,3,4}, values[] = {1500,2000,3000}, sizes[] = {2,5,3}
• dp[i][j] = max( k * values[i] + dp[i - 1][j - k * weights[i]] )，条件： k * weights[i] <= j 并且 0 <= k <= sizes[i]，遍历每一个 k
• k：对于第 i 类物品，可以取0、1、2等个数

代码实现

代码实现1：普通dp，增加一行

public int getMaxValue(int[] weights, int[] values, int[] sizes, int total) {
	int[][] dp = new int[weights.length + 1][total + 1];
	for (int i = 1; i <= weights.length; i ++) {
		for (int j = 1; j <= total; j ++) {
			// 枚举可以放 k 个第 i 类物品
			for (int k = 0; k <= sizes[i - 1] && k * weights[i - 1] <= j; k ++) {
				dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - k * weights[i - 1]] + k * values[i - 1]);
			}
		}
	}
	return dp[weights.length][total];
}

代码实现2：空间优化，从后往前遍历背包，dp[i]只与dp[i - 1]有关

// 增加一行
public int getMaxValue(int[] weights, int[] values, int[] sizes, int total) {
	int[] dp = new int[total + 1];
	for (int i = 1; i <= weights.length; i ++) {
		for (int j = total; j >= 1; j --) {
			// 枚举可以放k个第i类物品
			for (int k = 0; k <= sizes[i - 1] && k * weights[i - 1]; k ++) {
				dp[j] = Math.max(dp[j], dp[j - k * weights[i - 1]] + k * values[i - 1]);
			}
		}
	}
	return dp[total];
}

代码实现3：二进制优化，转化为0-1背包

public int getMaxValue(int[] weights, int[] values, int[] sizes, int total) {
    int size = weights.length;
    // 某类物品有7个，1到7最少需要log2(7)向上取整：3个数来表示，即1、2、4
    // 某类物品有10个，1到10最少需要log2(10)向上取整：4个数来表示，即1、2、4、3（1、2、4组成的最大值是7，10 - 7 = 3）
    List<Integer> weightsList = new ArrayList<>();
    List<Integer> valuesList = new ArrayList<>();
    for (int i = 0; i < size; i ++) {
        for (int j = 1; j <= sizes[i]; j <<= 1) {
            sizes[i] -= j;
            weightsList.add(j * weights[i]);
            valuesList.add(j * values[i]);
        }
        if (sizes[i] > 0) {
            weightsList.add(sizes[i] * weights[i]);
            valuesList.add(sizes[i] * values[i]);
        }
    }
    
    // 此时转换为0 - 1背包
    int newSize= weightsList.size();
    int[] dp = new int[newSize + 1];
    for (int i = 0; i < newSize; i ++) {
        for (int j = total; j >= weightsList.get(i); j --) {                                
            dp[j] = Math.max(dp[j], dp[j - weightsList.get(i)] + valuesList.get(i));                
        }
    }
    return dp[newSize];

}

代码实现4：单调队列优化（https://www.acwing.com/solution/content/6500/）

3.1.2.4 空间优化总结

动态规划问题，基于「自底向上」、「空间换时间」的思想，通常是「填表格」。

参考链接：动态规划（理解无后效性）

由于通常只关心最后一个状态值，或者在状态转移的时候，当前值只参考了上一行的值，因此在填表的过程中，表格可以复用，常用的技巧有：

• 滚动数组（当前行只参考了上一行的时候，可以只用 2 行表格完成全部的计算）
• 滚动变量（斐波拉契数列问题）

「表格复用」的合理性，只由「状态转移方程」决定，即当前状态值只参考了哪些部分的值。掌握非常重要的「表格复用」技巧：

• 「0-1 背包问题」（弄清楚为什么要倒序填表）
• 「完全背包问题」（弄清楚为什么可以正向填表）

3.1.2.5 其他问题

• 求恰好装满：dp[0,…,n][0] 初始化为0，其他dp值全初始化为 -1（表明还没有合法的解）
• 求方案总数：状态转移中的max改为sum
• 二维背包：增加dp维数
• 求最优方案：多开辟一个数组记录state[][]每个dp状态是怎么转移来的，比如state[i][j] = 0 表明dp[i][j]是不放物品得到的，state[i][j] = 1 表明dp[i][j]是放物品得到的

3.2 区间DP

思考的时候可以先将大区间拆分成小区间，求解的时候由小区间的解得到大区间的解

• 核心思路：拆分大区间可以通过枚举区间长度实现

// 枚举区间长度
for (int len = 1; len <= n; ++len) {
    // i <= n - len (n - 1) + 1
    // 枚举区间起点
    for (int i = 1; i <= n - len + 1; ++i) {
    	// 区间终点
        int j = i + len - 1;
        for (int k = i + 1; k < j; k++) {
            dp[i][j] = max(dp[i][j], dp[i][k] + dp[k][j] + nums[k] * nums[i - 1] * nums[j + 1]);
        }
    }
}

LeetCode 5. 最长回文子串

LeetCode 1143. 最长公共子序列

LeetCode 877. 石子游戏

LeetCode 72. 编辑距离

LeetCode 10. 正则表达式匹配

3.3 树形DP

3.4 状压DP

3.5 数位DP

统计给定区间上满足一些条件的数的个数

LeetCode 233. 数字 1 的个数

给定一个整数 n，计算所有小于等于 n 的非负整数中数字 1 出现的个数。

示例：

输入: 13
输出: 6 
解释: 数字 1 出现在以下数字中: 1, 10, 11, 12, 13 。

洛谷 P2657 [SCOI2009] windy 数

不含前导零且相邻两个数字之差至少为 22 的正整数被称为 windy 数。windy 想知道，在 aa 和 bb 之间，包括 aa 和 bb ，总共有多少个 windy 数？

示例：

输入[1,10]，输出9
输入[25,50]，输出20
对于全部的测试点，保证 1 <= a <= b <= 2×10^9

洛谷 P2602 [ZJOI2010]数字计数

给定两个正整数 a 和 b，求在 [a,b]中的所有整数中，每个数码(digit)各出现了多少次

示例：

输入：[1,99] 输出：9 20 20 20 20 20 20 20 20 20

LeetCode 902. 最大为 N 的数字组合

LeetCode 1012. 至少有 1 位重复的数字