AutoCV番外:Transformer
目录
- Transformer
-
- 注意事项
- 一、2023/5/16更新
- 前言
- 1. Self-attention
-
- 1.1 前置知识
- 1.2 Self-attention机制
- 1.3 矩阵乘法角度理解
- 1.4 Multi-head Self-attention
- 1.5 Positional Encoding
- 1.6 Many application
- 2. Transformer
-
- 2.1 前置知识
- 2.2 Encoder
- 2.3 AT Decoder
- 2.4 NAT Decoder
- 2.5 Cross attention
- 2.6 Training
- 3. 实战
-
- 3.1 Prelims
- 3.2 Model Architecture
-
- 3.2.1 Encoder
- 3.2.2 Decoder
- 3.2.3 Attention
- 3.2.4 Position-wise Feed-Forward Networks
- 3.2.5 Embeddings and Softmax
- 3.2.6 Positional Encoding
- 3.2.7 Full Model
- 3.2.8 Inference
- 3.3 Model Training
-
- 3.3.1 Batches and Masking
- 3.3.2 Training Loop
- 3.3.3 Optimizer
- 3.3.4 Regularization
- 3.4 实战总结
- 总结
Transformer
注意事项
一、2023/5/16更新
更新 Transformer 实战,手写复现,即第 3 节内容
前言
AutoCV 之后的课程中需要学习到 BEVFormer 先对 Transformer 做一个简单的了解
关于 Self-attention 和 Transformer 的内容均来自于李宏毅老师的视频讲解
视频链接:【机器学习2021】自注意力机制(Self-attention) 【机器学习2021】Transformer
1. Self-attention
聊 Transformer 之前需要聊聊 Self-attention。
以下内容均来自于李宏毅老师的 Self-attention 的视频讲解
视频链接:【机器学习2021】自注意力机制(self-attention)
1.1 前置知识
self-attention 解决的是输入的数目和序列长度不一致的问题,那在实际中有哪些应用会将一个向量集合 (Vector Set) 作为输入呢?

图1-1 中对比了输入是简单 vector 和 复杂 vector set 两种情形。常见输入都是简单的 vector 应用有比如让你对 2023 年上海房价进行预测,比如给你一张图片需要你判断是那个动物等等。那也有输入是一个 vector set 形式,比如 chat Bot 聊天机器人,用户每次都会提供不同的问题,比如机器翻译,比如语言情感分析等等。
在文字处理方面,其输入常常是一句话或者一段话,比如当用户向 chatGPT 提问时,由于每次的问题都不一样,导致每次的输入都不同。self-attention 就是被用来处理这种问题的。
在正式介绍 self-attention 之前,我们需要了解到为了方便计算机的处理和计算,同时让计算机捕捉和理解词汇之间的语义关系,我们通常需要将一个词汇用一个向量表示。那么怎么把一个词汇描述为一个向量呢?
常见的有 one-hot encoding 和 Word Embedding 方法,如 图1-2 所示
ont-hot encoding
-
最先想到的可能就是 ont-hot 编码,考虑所有的词汇,比如常见的 3000 个单词,那么就编码为一个 3000 维的向量,每个词汇都在对应的位置设置为 1,其它设置为 0
-
但是这种方法存在一个严重的问题:它假设所有词汇之间都是没有关系的,所以无法表达词汇之间的语义相似性,即从 One-hot Encoding 中你看不出来说 cat 和 dog 都是动物所有比较相像,cat 和 apple 一个动物一个植物所以比较不相像,这个向量里面是不存在任何语义信息,而且每个词汇向量的维度非常高,将会导致计算和存储的复杂性
Word Embedding
-
词嵌入方法,它会分配给每一个词汇一个向量,那么一个句子就是一个长度不一的向量,具体的实现不是这里讲解的重点,可自行学习
-
更多细节:https://www.youtube.com/watch?v=X7PH3NuYW0Q
知道了输入是一个 vector set,那么对应的输出也有以下几种可能,见 图1-3
- Each vector has a label
- 每个向量都有一个对应的标签,比如输入 4 个向量,输出 4 个标签
- 比如在 Pos tagging 词性标注问题上,对于每个词汇给出对应的词性,例如
I saw a saw其对应的输出为N V DET N
- The whole sequence has a label
- 整个序列只有一个标签
- 比如在 Sentiment analysis 情感分析问题上,对于一段话机器需要给出它是 positive 还是 negative
- Model decides the number of labels itself
- 模型自己决定输出标签的数量
- sequence to sequence 任务,比如 chatGPT
我们现在只考虑第一种情形,即每个向量都有一个标签,这个任务又叫做 Sequence Labeling,那么如何去解决这个问题呢?
比较容易想到的就是我们把每一个 vector 分别输入到全连接的网络里面,逐个击破,见 图1-4 但是这样会存在一个很大的问题。假如是词性标记问题,对 I saw a saw 进行标记,对全连接网络来说第一个 saw 和第二个 saw 完全一模一样呀,它们都是同一个词汇,因此网络没有理由会有不同的输出,而实际上你想要你第一个 saw 输出动词,第二个 saw 输出名词,而对于 FC 来说不可能做到。
那怎么办呢?有没有可能让 FC 考虑 contex 上下文信息呢?
是有可能的,我们将前后向量都串起来一起丢到 Fully-Connected Network 中就可以了,如 图1-5 所示
所以我们可以给 Fully-Connected Network 一整个 window 的信息,让它可以考虑一些上下文,考虑与目前向量相邻的其它向量的信息。
但是如果我们有一个任务,不是考虑一个 window 的 context 就可以解决,而是要考虑一整个 sequence 的 context 才能解决,那怎么办呢?
那有人可能会想说这个还不容易,我就把 window 开大一点嘛,大到可以覆盖整个 sequence,但是我们输入给 model 的 sequence 有长有短,每次都可能不一样,那么就可能需要统计下你的训练集,看下其中最长的 sequence 有多长,然后开一个比最长的 sequence 更大的 window,但是你开一个这么大的 window 意味着你的 Fully-connected Network 需要非常多的参数,不但计算量大,可能还容易 Overfitting
所以有没有更好的方法来考虑整个 input sequence 的信息呢?这就是接下来要介绍的 self-attention 这个技术
1.2 Self-attention机制
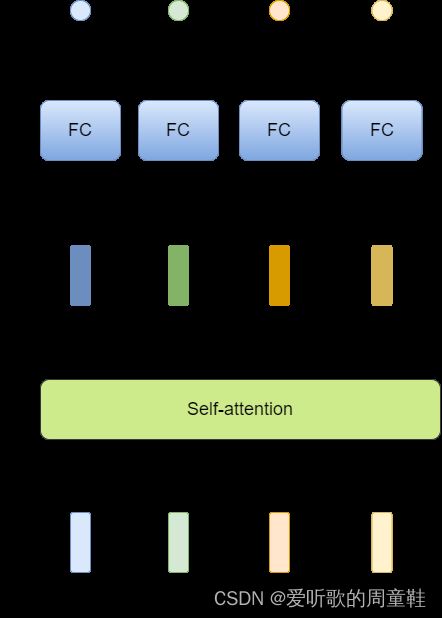
self-attention的运作方式就是吃一整个 sequence 的信息,然后你输入多少个 vector,它就输出多少个 vector
经过 self-attention 后的 4 个 vector 都是考虑了一整个 sequence 以后才得到的,再把这些考虑了整个句子的 vector 丢到 Fully-Connected Network 中得到最终的输出,如此一来,你的 Fully-Connected Network 它就不是只考虑一个非常小的范围或一个小的 window,而是考虑整个 sequence 的信息,再来决定现在应该要输出什么样的结果,这个就是 self-attention。
当然你可以使用多次 self-attention,将 self-attention 和 Fully-Connected Network 交替使用,self-attention 来处理整个 sequence 的信息,而 Fully-Connected Network 专注于处理某一个位置的信息
有关于 self-attention 最知名的相关文章就是 Attention is all you need,在这篇文章中,Google 提出了我们熟知的 Transformer 这样的 Network 架构,Transformer 里面最重要的一个 Module 就是 self-attention。
讲了这么久,那 self-attention 到底是怎么运作的呢?
self-attention 的 input 就是一串 vector,而这个 vector 可能是你整个 Network 的 input,也有可能是某个 hidden layer 的 output,用 a \boldsymbol a a 来表示而不是用 x \boldsymbol x x 来表示,代表说它有可能前面已经做过一些处理,input 一排 a \boldsymbol a a 向量之后,self-attention 需要 output 另外一排 b \boldsymbol b b 向量,每个 b \boldsymbol b b 都是考虑了所有的 a \boldsymbol a a 生成出来的
接下来就是来说明怎么产生 b 1 \boldsymbol b^{\boldsymbol 1} b1 这个向量,知道怎么产生 b 1 \boldsymbol b^{\boldsymbol 1} b1 向量以后, b 2 \boldsymbol b^{\boldsymbol 2} b2 b 3 \boldsymbol b^{\boldsymbol 3} b3 b 4 \boldsymbol b^{\boldsymbol 4} b4 的产生你也就知道了,那么怎么产生 b 1 \boldsymbol b^{\boldsymbol 1} b1 呢?
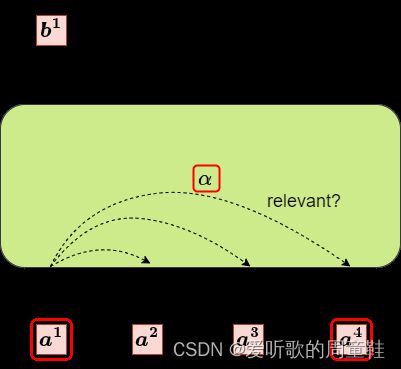
首先根据 a 1 \boldsymbol a^{\boldsymbol 1} a1 找到 sequence 里面跟 a 1 \boldsymbol a^{\boldsymbol 1} a1 相关的其它向量。我们做 self-attention 的目的是为了考虑整个 sequence,但是我们又不希望将所有的信息放在一个 window 里面,所有我们有一个特别的机制,这个机制就是说找出整个很长的 sequence 里面到底哪些部分是重要的,哪些部分跟判断 a 1 \boldsymbol a^{\boldsymbol 1} a1 是哪一个 label 是有关系的。
那么每一个向量跟 a 1 \boldsymbol a^{\boldsymbol 1} a1 的关联程度我们用一个数值 α \alpha α 来表示,接下来的问题就是 self-attention 这个 module 怎么自动决定两个向量之间的关联性呢?比如你给它两个向量 a 1 \boldsymbol a^{\boldsymbol 1} a1 和 a 4 \boldsymbol a^{\boldsymbol 4} a4,它怎么决定 a 1 \boldsymbol a^{\boldsymbol 1} a1 跟 a 4 \boldsymbol a^{\boldsymbol 4} a4 有多相关,然后给它一个数值 α \alpha α 呢?
那么这边你就需要一个计算 attention 的模块,它的输入是两个向量,直接输出 α \alpha α 数值,你就可以把 α \alpha α 数值当做两个向量的关联的程度,那具体怎么计算这个 α \alpha α 数值呢?比较常见的做法有 dot-product 和 Additive
dot-product
- 把输入的两个向量分别乘以两个不同的矩阵 W q W^q Wq 和 W k W^k Wk,左边向量乘以 W q W^q Wq 这个矩阵,右边向量乘以 W k W^k Wk 这个矩阵,接下来得到 q \boldsymbol q q 跟 k \boldsymbol k k 这两个向量
- 再把 q \boldsymbol q q 跟 k \boldsymbol k k 做 dot product,就是把它们做 element-wise 相乘再相加得到 α \alpha α
Additive
- 同样把输入的两个向量分别乘以两个不同的矩阵 W q W^q Wq 和 W k W^k Wk,得到 q \boldsymbol q q 跟 k \boldsymbol k k 这两个向量
- 然后串起来丢到 t a n h tanh tanh 函数中,再经过一个 Transform 得到 α \alpha α
总之有非常多不同的方法可以计算 Attention,可以计算这个 α \alpha α 的数值,可以计算这个关联的程度,但是在接下来的讨论里面我们都只用左边 dot-product 这个方法,这是目前最常用的方法,也是 Transformer 里面的方法。
接下来怎么把它套用到 self-attention 里面呢?对于 a 1 \boldsymbol a^{\boldsymbol 1} a1 需要分别计算它与 a 2 \boldsymbol a^{\boldsymbol 2} a2 a 3 \boldsymbol a^{\boldsymbol 3} a3 a 4 \boldsymbol a^{\boldsymbol 4} a4 之间的关联性,也就是计算它们之间的 α \alpha α,那怎么做呢?
你把 a 1 \boldsymbol a^{\boldsymbol 1} a1 乘上 W q W^q Wq 得到 q 1 \boldsymbol q^{\boldsymbol 1} q1,这个 q \boldsymbol q q 有个名字叫做 Query,也就是搜寻查询的意思,然后接下来对于 a 2 \boldsymbol a^{\boldsymbol 2} a2 a 3 \boldsymbol a^{\boldsymbol 3} a3 a 4 \boldsymbol a^{\boldsymbol 4} a4 你都要去把它乘上 W k W^k Wk 得到 k \boldsymbol k k 这个 vector,这个 k \boldsymbol k k 有个名字叫做 Key,也就是关键字的意思。那你把这个 Query q 1 \boldsymbol q^{\boldsymbol 1} q1 和这个 Key k 2 \boldsymbol k^{\boldsymbol 2} k2 计算 inner product 就得到 α 1 , 2 \alpha_{1,2} α1,2,代表向量 1 和向量 2 之间的相关性,其中 Query 是由向量 1 提供,Key 是由向量 2 提供, α \alpha α 关联性也有一个名称叫做 attention score
同理可计算出 α 1 , 3 \alpha_{1,3} α1,3 α 1 , 4 \alpha_{1,4} α1,4,如 图1-11 所示
其实一般在实际应用中, q 1 \boldsymbol q^{\boldsymbol 1} q1 也会和自己计算关联性,所以你也要把 a 1 \boldsymbol a^{\boldsymbol 1} a1 乘上 W k W^k Wk 得到 k 1 \boldsymbol k^{\boldsymbol 1} k1,然后计算它的关联性 α 1 , 1 \alpha_{1,1} α1,1
我们算出 a 1 \boldsymbol a^{\boldsymbol 1} a1 和每个向量的关联性之和,接下来会做一个 softmax,输出为一组 α ′ \alpha' α′,在这边不一定要用 softmax,你可以尝试用别的东西也没有问题,比如 ReLU,
得到 α ′ \alpha' α′ 以后,我们就要根据 α ′ \alpha' α′ 抽取出 sequence 里面重要的信息,接下来我们要根据关联性,根据这个 attention 的分数来抽取重要的信息,怎么抽取重要的信息呢?
我们会把 a 1 \boldsymbol a^{\boldsymbol 1} a1 到 a 4 \boldsymbol a^{\boldsymbol 4} a4 这边每一个向量乘上 W v W^v Wv 得到新的向量,分别用 v 1 \boldsymbol v^{\boldsymbol 1} v1 v 2 \boldsymbol v^{\boldsymbol 2} v2 v 3 \boldsymbol v^{\boldsymbol 3} v3 v 4 \boldsymbol v^{\boldsymbol 4} v4 来表示,接下来把 v 1 \boldsymbol v^{\boldsymbol 1} v1 v 2 \boldsymbol v^{\boldsymbol 2} v2 v 3 \boldsymbol v^{\boldsymbol 3} v3 v 4 \boldsymbol v^{\boldsymbol 4} v4 每一个向量都去乘上 attention 的分数,都去乘上 α ′ \alpha' α′ 然后再把它加起来得到 b 1 \boldsymbol b^{\boldsymbol 1} b1
如果某一个向量它得到的分数越高,比如 a 1 \boldsymbol a^{\boldsymbol 1} a1 和 a 2 \boldsymbol a^{\boldsymbol 2} a2 的关联性很强,这个 α 1 , 2 ′ \alpha'_{1,2} α1,2′ 得到的值就很大,那我们在做 Weighted Sum 以后得到的 b 1 \boldsymbol b^{\boldsymbol 1} b1 的值就可能比较接近 v 2 \boldsymbol v^{\boldsymbol 2} v2,所有这边谁的 attention 的分数越大,谁的 v \boldsymbol v v 就会 Dominant 你抽出来的结果。
OK! 到这边我们讲解了怎么从一整个 sequence 得到 b 1 \boldsymbol b^{\boldsymbol 1} b1
这边需要强调的是 b 1 \boldsymbol b^{\boldsymbol 1} b1 到 b 4 \boldsymbol b^{\boldsymbol 4} b4 并不需要顺序产生,你并不需要算完 b 1 \boldsymbol b^{\boldsymbol 1} b1 再算 b 2 \boldsymbol b^{ \boldsymbol 2} b2 再算 b 3 \boldsymbol b^{\boldsymbol 3} b3 再算 b 4 \boldsymbol b^{\boldsymbol 4} b4, b 1 \boldsymbol b^{\boldsymbol 1} b1 到 b 4 \boldsymbol b^{\boldsymbol 4} b4 它们是一次同时被计算出来的。
1.3 矩阵乘法角度理解
从 a 1 \boldsymbol a^{\boldsymbol 1} a1 到 a 4 \boldsymbol a^{\boldsymbol 4} a4 得到 b 1 \boldsymbol b^{\boldsymbol 1} b1 到 b 4 \boldsymbol b^{\boldsymbol 4} b4 是 self-attention 的运作过程,接下来我们从矩阵乘法的角度再重新讲一次我们刚才讲的 self-attention 是怎么运作的。
我们知道每一个 a \boldsymbol a a 都要分别产生 q \boldsymbol q q k \boldsymbol k k v \boldsymbol v v,如果用矩阵运算表示这个操作的话是什么样子呢?
q i = W q a i \boldsymbol q^{\boldsymbol i} = W^q \boldsymbol a^{\boldsymbol i} qi=Wqai
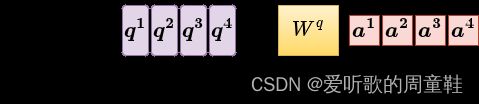
每一个 a \boldsymbol a a 都要乘上 W q W^q Wq 得到 q \boldsymbol q q,那么我们可以把 a 1 \boldsymbol a^{\boldsymbol 1} a1 到 a 4 \boldsymbol a^{\boldsymbol 4} a4 拼起来看作是一个矩阵用 I I I 来表示,而矩阵 I I I 有四列,每一列就是 a 1 \boldsymbol a^{\boldsymbol 1} a1 到 a 4 \boldsymbol a^{\boldsymbol 4} a4,那 I I I 乘上 W q W^q Wq 就得到另一一个矩阵,我们用 Q Q Q 来表示, Q Q Q 就是 q 1 \boldsymbol q^{\boldsymbol 1} q1 到 q 4 \boldsymbol q^{\boldsymbol 4} q4
所以我们从 a 1 \boldsymbol a^{\boldsymbol 1} a1 到 a 4 \boldsymbol a^{\boldsymbol 4} a4 得到 q 1 \boldsymbol q^{\boldsymbol 1} q1 到 q 4 \boldsymbol q^{\boldsymbol 4} q4 这件事情就是把矩阵 I I I 也就是我们的 input 乘上另外一个矩阵 W q W^q Wq,而 W q W^q Wq 其实是 Network 的参数,把 I I I 乘上 W q W^q Wq 就得到 Q Q Q,而 Q Q Q 的四个 column 就是 q 1 \boldsymbol q^{\boldsymbol 1} q1 到 q 4 \boldsymbol q^{\boldsymbol 4} q4
那么接下来怎么产生 k \boldsymbol k k 和 v \boldsymbol v v 呢?它的操作其实跟 q \boldsymbol q q 是一模一样的,如 图1-17 所示:
所以每一个 a \boldsymbol a a 怎么得到 q \boldsymbol q q k \boldsymbol k k v \boldsymbol v v 呢?其实就是把输入的这个 vector set 乘上三个不同的矩阵,你就得到了 q \boldsymbol q q k \boldsymbol k k v \boldsymbol v v
那么接下来每一个 q \boldsymbol q q 都会去跟每一个 k \boldsymbol k k 去计算 inner product 得到 attention 的分数,那得到 attention score 这件事情,如果从矩阵操作的角度来看,它在做什么样的事情呢?
比如 α 1 , i = ( k i ) T q 1 \alpha_{1,i} = (\boldsymbol k^{\boldsymbol i})^T \boldsymbol q^{\boldsymbol 1} α1,i=(ki)Tq1,我们可以将 k 1 \boldsymbol k^{\boldsymbol 1} k1 到 k 4 \boldsymbol k^{\boldsymbol 4} k4 拼接起来看作是一个矩阵的四个 row,再把这个矩阵乘上 q 1 \boldsymbol q^{\boldsymbol 1} q1 就得到另外一个向量,这个向量里面的值就是 attention score, α 1 , 1 \alpha_{1,1} α1,1 到 α 1 , 4 \alpha_{1,4} α1,4
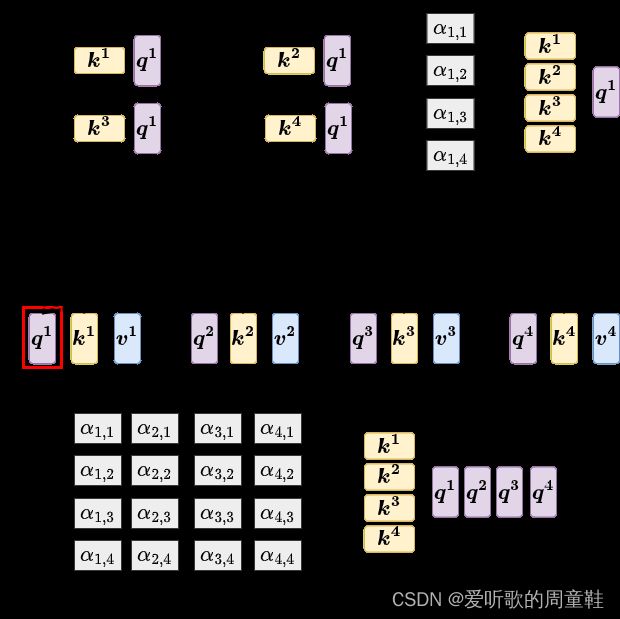
我们不止是 q 1 \boldsymbol q^{\boldsymbol 1} q1 要对 k 1 \boldsymbol k^{\boldsymbol 1} k1 到 k 4 \boldsymbol k^{\boldsymbol 4} k4 去计算 attention score,还有 q 2 \boldsymbol q^{\boldsymbol 2} q2 q 3 \boldsymbol q^{\boldsymbol 3} q3 q 4 \boldsymbol q^{\boldsymbol 4} q4 也要按照上述流程计算 attention score
那么这些 attention scores 是怎么计算得来的?你可以看作是两个矩阵 K K K 和 Q Q Q 的相乘,一个矩阵的 row 就是 k 1 \boldsymbol k^{\boldsymbol 1} k1 到 k 4 \boldsymbol k^{\boldsymbol 4} k4,另外一个矩阵的 column 就是 q 1 \boldsymbol q^{\boldsymbol 1} q1 到 q 4 \boldsymbol q^{\boldsymbol 4} q4,得到矩阵 A A A,那矩阵 A A A 存储的就是 Q Q Q 跟 K K K 之间 的 attention 分数
那么接下来我们会对 attention 的分数做一下 normalization,对这边的每一个 column 做 softmax,使得每一个 column 的值相加为 1,前面有提到过做 softmax 并不是唯一的选项,当然你完全可以选择其它的操作,比如说 ReLU 之类的,得到的结果也不会比较差
接下来,我们需要通过 attention 分数矩阵 A ′ A' A′ 计算得到 b \boldsymbol b b,那么 b \boldsymbol b b 是怎么被计算出来的呢?你就把 v 1 \boldsymbol v^{\boldsymbol 1} v1 到 v 4 \boldsymbol v^{\boldsymbol 4} v4 拼起来,当成是 V V V 矩阵的四个 column,然后让 V V V 乘上 A ′ A' A′ 得到最终的输出矩阵 O O O
O O O 矩阵里面的每一个 column 就是 self-attention 的输出,也就是 b 1 \boldsymbol b^{\boldsymbol 1} b1 到 b 4 \boldsymbol b^{\boldsymbol 4} b4
所以说 self-attention 的整个操作是先产生了 q \boldsymbol q q k \boldsymbol k k v \boldsymbol v v,然后再根据 q \boldsymbol q q 去找出相关的位置,然后再对 v \boldsymbol v v 做 weighted sum,其实这一串操作就是一连串矩阵的乘法而已
其中 I I I 是 self-attention 的 input,是一组 vector,即 vector set,这组 vector 拼起来当作矩阵 I I I 的 column,那这个 input 分别乘上三个矩阵 W q W^q Wq W k W^k Wk W v W^v Wv 得到 Q Q Q K K K V V V 三个矩阵,接下来 Q Q Q 乘上 K T K^T KT 得到矩阵 A A A,矩阵 A A A 经过一些处理得到 A ′ A' A′,我们会把 A ′ A' A′ 称作 Attention Matrix,最后将 A ′ A' A′ 乘上 V V V 得到 O O O, O O O 就是 self-attention 这个 layer 的输出。所以 self-attention 输入是 I I I 输出是 O O O,self-attention 中唯一需要学习的参数就是 W q W^q Wq W k W^k Wk W v W^v Wv,是通过 training data 找出来的。
1.4 Multi-head Self-attention
self-attention 它还有一个进阶的版本叫做 Multi-head Self-attention,它在现在的使用非常广泛。在机器翻译、在语音辨识任务用比较多的 head 反而可以得到比较好的结果,至于需要多少的 head,这又是一个 hyperparameter 需要自己去调节。
那为什么需要多 head 呢?在 self-attention 中我们通过 q \boldsymbol q q 去寻找相关的 k \boldsymbol k k,但相关这件事情有很多种不同的形式,有很多种不同的定义。所以也许我们不能只有一个 q \boldsymbol q q,我们应该要有多个 q \boldsymbol q q,不同的 q \boldsymbol q q 负责不同种类的相关性。
所以如果你要做 Multi-head Self-attention 的话,你先把 a \boldsymbol a a 乘上一个矩阵得到 q \boldsymbol q q,接下来你再把 q \boldsymbol q q 乘上另外两个矩阵分别得到 q i , 1 \boldsymbol q^{\boldsymbol {i,1}} qi,1 和 q i , 2 \boldsymbol q^{\boldsymbol {i,2}} qi,2,其中 i \boldsymbol i i 代表的是位置,1 和 2 代表的是这个位置的第几个 q \boldsymbol q q
图1-23 中代表说我们有两个 head,我们认为这个问题里面有两种不同的相关性,是我们需要产生两种不同的 head 来找两种不同的相关性,既然 q \boldsymbol q q 有两个,那么对应的 k \boldsymbol k k 和 v \boldsymbol v v 也需要有两个,所以对另外一个位置也做相同的事情,也会得到两个 q \boldsymbol q q 两个 k \boldsymbol k k 两个 v \boldsymbol v v
那怎么做 self-attention 呢?还是和我们之前讲的操作是一模一样的,只是 1 那一类的一起做,2 那一类的一起做,也就是说 q 1 \boldsymbol q^{\boldsymbol 1} q1 在计算 attention score 的时候就不需要管 k 2 \boldsymbol k^{\boldsymbol 2} k2 了,它就只管 k 1 \boldsymbol k^{\boldsymbol 1} k1 就好
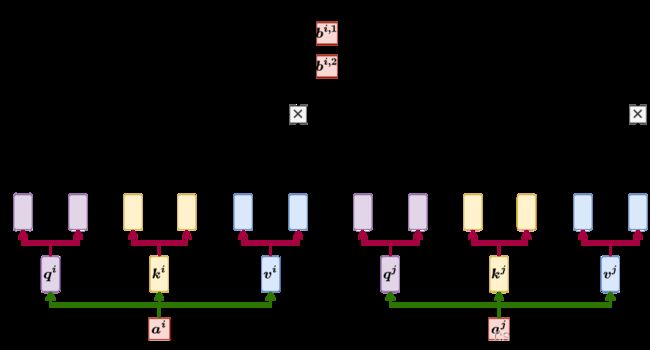
所以 q i , 1 \boldsymbol q^{\boldsymbol {i,1}} qi,1 就跟 k i , 1 \boldsymbol k^{\boldsymbol {i,1}} ki,1 算 attention, q i , 1 \boldsymbol q^{\boldsymbol {i,1}} qi,1 就跟 k j , 1 \boldsymbol k^{\boldsymbol {j,1}} kj,1 算 attention,得到 attention score,在计算 weighted sum 的时候也不要管 v 2 \boldsymbol v^{\boldsymbol 2} v2 了,看 v i , 1 \boldsymbol v^{\boldsymbol {i,1}} vi,1 跟 v j , 1 \boldsymbol v^{\boldsymbol {j,1}} vj,1 就好,所以你把 attention 的分数乘以 v i , 1 \boldsymbol v^{\boldsymbol {i,1}} vi,1,把 attention 的分数乘以 v j , 1 \boldsymbol v^{\boldsymbol {j,1}} vj,1,接下来就得到了 b i , 1 \boldsymbol b^{\boldsymbol {i,1}} bi,1 如 图1-25 所示
这边只用了其中一个 head,那也可以用另外一个 head 也做一模一样的事情去计算 b i , 2 \boldsymbol b^{\boldsymbol {i,2}} bi,2 如 图1-26 所示
如果你有 8 个 head,有 16 个 head 也是同样的操作,这里是以两个 head 作为例子来演示。
接下来你可能会把 b i , 1 \boldsymbol b^{\boldsymbol {i,1}} bi,1 跟 b i , 2 \boldsymbol b^{\boldsymbol {i,2}} bi,2 拼接起来,然后再通过一个 transform 得到 b i \boldsymbol b^{\boldsymbol i} bi,然后送到下一层去。
这个就是 Multi-head attention,self-attention 的一个变形
1.5 Positional Encoding
那讲到目前为止,你会发现说 self-attention 的这个 layer 少了一个也许很重要的信息,这个信息就是位置的信息,对于一个 self-attention 而言,每一个 input 它是出现在 sequence 的最前面还是最后面,它是完全没有这个信息的,对不对。
对于 self-attention 而言,1 和 4 的距离并没有非常远,2 和 3 的距离也没有说非常近,所有的位置之间的距离都是一样的,没有任何一个位置距离比较远,也没有任何位置距离比较近。
但是这样子的设计可能存在一些问题,因为有时候位置的信息也许很重要,举例来说,我们在做这个 POS tagging 词性标记的时候,也许你知道说动词比较不容易出现在句首,所以我们知道说某一个词汇它是放在句首,那它是动词的可能性就比较低,会不会这样子的位置的信息往往也是有用的呢?
到目前为止我们讲到的 self-attention 的操作里面,它根本就没有位置的信息,所以你在做 self-attention 的时候,如果你觉得位置信息是一个重要的事情,那你可以把位置的信息把它塞进去。
怎么把位置的信息塞进去呢?这边就要用到一个叫做 positional encoding 的技术。你需要为每一个位置设定一个 vector 叫做 positional vector,这边用 e i \boldsymbol e^{\boldsymbol i} ei 来表示,上标 i \boldsymbol i i 代表位置,每一个不同的位置就有不同的 vector,比如 e 1 \boldsymbol e^{\boldsymbol 1} e1 是一个 vector, e 2 \boldsymbol e^{\boldsymbol 2} e2 是一个 vector, e 128 \boldsymbol e^{\boldsymbol {128}} e128 也是一个 vector,不同的位置都有一个专属的 e \boldsymbol e e,然后把这个 e \boldsymbol e e 加到 a i \boldsymbol a^{\boldsymbol i} ai 上就结束了。
上述操作就等于告诉 self-attention 位置的信息,如果它看到说 a i \boldsymbol a^{\boldsymbol i} ai 有被加上 e i \boldsymbol e^{\boldsymbol i} ei 它就知道说现在出现的位置应该是在 i \boldsymbol i i 这个位置,那这个 e i \boldsymbol e^{\boldsymbol i} ei 是什么样子呢?最早的这个 transformer 也就是 Attention is all you need 那篇 paper 里面,它用的 e i \boldsymbol e^{\boldsymbol i} ei 如 图1-29 所示
它的每一个 column 就代表一个 e \boldsymbol e e,第一个位置就是 e 1 \boldsymbol e^{\boldsymbol 1} e1 第二个位置就是 e 2 \boldsymbol e^{\boldsymbol 2} e2 以此类推,每一个位置都有一个专属的 e \boldsymbol e e,希望透过给每一个位置不同的 e \boldsymbol e e,你的 model 在处理这个 input 的时候,它可以知道现在的 input 它的位置的信息是什么样子
这样子的 positional vector 它是 hand-crafted 也就是人为设定的,那人设的 vector 就存在很多问题呀,就假设我现在在定这个 vector 的时候只定到 128,那我现在 sequence 的长度如果是 129 怎么办呢?不过在 Attention is all you need 那篇 paper 里面是没有这个问题的,它这个 vector 是透过某一种规则所产生的,透过一个很神奇的 sin cos 的 function 所产生的。其实你也不一定非要这么产生,这个 positional encoding 仍然是一个尚待研究的问题,你可以创造新的方法,甚至说是可以 learned from data
1.6 Many application
那这个 self-attention 当然是用得很广,比如 transformer 这个东西,比如在 NLP 领域有一个东西叫做 BERT,BERT 里面也有用到 self-attention,所以 self-attention 在 NLP 上的应用是大家都耳熟能详的
但 self-attention 不只是可以用在 NLP 相关的应用上,它还可以用在很多其它的问题上,比如语音辨识、图像任务,例如 Truncated Self-attention、Self-Attention GAN、DEtection Transformer(DETR)
那好,接下来我们来对比下 Self-attention 和 CNN 之间的差异或者关联性
如果我们用 self-attention 来处理一张图片,代表说假设你要处理一个 pixel,那它产生 query,其它 pixel 产生 key,你在做 inner product 的时候,你考虑得不是一个小的区域,而是整张图片的信息。
但是在做 CNN 的时候我们会画出一个 receptive field,每一个 filter 只考虑 receptive field 范围里面的信息,所以我们比较 CNN 和 self attention 的话,我们可以说 CNN 可以看作是一种简化版的 self attention,因为在做 CNN 的时候,我们只考虑 receptive field 里面的信息,而在做 self attention 的时候,我们是考虑整张图片的信息。所以说 CNN 是一个简化版的 self attention
或者你可以反过来说,self-attention 是一个复杂化的 CNN,在 CNN 里面,我们要划定 receptive field,每一个 filter 只考虑 receptive field 里面的信息,而 receptive field 的范围和大小是人决定的。而对 self-attention 而言,我们用 attention 去找出相关的 pixel,就好像是 receptive field 是自动被学出来的,network 自己决定说 receptive field 的形状长什么样子,network 自己决定说以某个 pixel 为中心,哪些 pixel 是我们真正需要考虑的,哪些 pixel 是相关的,所以 receptive field 的范围不再是人工划定,而是让机器自己学出来。
更多细节:On the Relationship between Self-Attention and Convolutional Layers
在上面这篇 paper 里面会用数学的方式严谨的告诉你说其实 CNN 就是 self-attention 的特例,self-attention 只要设定合适的参数,它就可以做到跟 CNN 一模一样的事情,所以 self-attention 是更 flexible 的 CNN,而 CNN 是有受限制的 self-attention,self-attention 只要透过某些设计、某些限制它就会变成 CNN
既然 CNN 是 self-attention 的一个 subset,self-attention 比较 flexible,比较 flexible 的 model 当然需要更多的 data,如果你的 data 不够,就有可能 overfitting,而小的 model,比较有限制的 model,它适合在 data 小的情形,它可能比较不会 overfitting
接下来我们再来对比下 Self-attention 和 RNN
RNN 和 self-attention 一样都是要处理 input 是一个 sequence 的状况,其 output 都是一个 vector,而且 output 的一排 vector 都会给到 Fully-Connected Network 做进一步的处理
那 self-attention 和 RNN 有什么不同呢?当然一个非常显而易见的不同就是说 self-attention 考虑了整个 sequence 的 vector,而 RNN 只考虑了左边已经输入的 vector,它没有考虑右边的 vector,但是 RNN 也可以是双向的,如果是双向的 RNN 的话其实也是可以看作考虑了整个 sequence 的 vector
但是我们假设把 RNN 的 output 和 self-attention 的 output 拿来做对比的话,就算你用双向的 RNN 还是有一些差别的,如 图1-32 所示,对于 RNN 来说假设最右边的 vector 要考虑最左边的这个输入,那它必须要将最左边的输入存到 memory 里面,然后接下来都不能够忘掉,一路带到最右边才能够在最后一个时间点被考虑,但对 self-attention 来说没有这个问题,它只要最左边输出一个 query 最右边输出一个 key,只要它们匹配起来就可以轻易的提取信息,这是 RNN 和 self-attention 一个不一样的地方。
还有另外一个更主要的不同是 RNN 在处理的时候,你 input 一排 sequence 然后 output 一排 sequence 的时候,RNN 是没有办法平行化的,你要先产生前面一个向量,才能产生后面一个向量,它没有办法一次处理,没有平行一次处理所有的 output。但 self-attention 有一个优势,是它可以平行处理所有的输出,你 input 一排 vector 再 output vector 的时候是平行产生的,并不需要等谁先运算完才把其它运算出来,每一个 vector 都是同时产生出来的,所以在运算速度方面 self-attention 会比 RNN 更有效率。
现在很多的应用都在把 RNN 的架构逐渐改成 self-attention 的架构了
更多细节:Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention
self-attention 拥有非常多的变形,self-attention 的运算量非常大,怎么减少 self-attention 的运算量是一个未来的重点。self-attention 最早是用到 Transformer 上面,所有在讲 Transformer 的时候,其实它指的就是这个 self-attention,广义的 Transformer 就是指 self-attention,所以后来各种各样 self-attention 的变形都叫做是 xxxformer,如 Linformer、Performer、Reformer 等等,那到底什么样的 self-attention 又快又好,这仍然是一个尚待解决的问题
更多细节:Long Range Arena: A Benchmark for Efficient Transformers Efficient Transformers: A Survey
2. Transformer
聊完 Self-attention 之后,接下来终于可以聊聊 Transformer 了
以下内容均来自于李宏毅老师的 Transformer 的视频讲解
视频链接:【机器学习2021】Transformer
2.1 前置知识
Transformer 是什么呢?Transformer 就是一个 Sequence-to-sequence(Seq2seq) 的 model,那 Seq2seq 的 model 又是什么呢?
我们之前在讲解 self-attention 的时候,如果你的 input 是一个 sequence,对应的 output 存在几种情况,一种是 input 和 output 的长度一样,一种是直接 output 一个东西,还有一种情况就是 Seq2seq model 需要解决的,我们不知道 output 多长,由模型自己决定 output 的长度
那有什么样的应用是我们需要用到这种 Seq2seq model,也就是 input 是一个 sequence,output 也是一个 sequence,但是我们不知道 output 的长度,应该由模型自己决定 output 的长度,如 图2-1 所示
一个很好的应用就是语音辨识,其输入是声音讯号,输出是语音所对应的文字,当然我们没有办法根据输入语音的长度推出 output 的长度,那怎么办呢?由模型自己决定,听一段语音,自己决定它应该要输出几个文字;还有一个应用就是机器翻译,让模型读一种语言的句子,输出另外一种语言的句子;甚至还有更复杂的应用,比如说语音翻译,给定一段语音 machine learning,它输出的不是英文,它直接把它听到的语音信号翻译成中文
在文字上你也可以用 Seq2seq model,举例来说你可以用 Seq2seq model 来训练一个聊天机器人,需要收集到大量的聊天训练数据,各式各样的 NLP 的问题都可以看作是 Question Answering(QA) 问题,而 QA 的问题就可以用 Seq2seq model 来解。必须要强调的是,对多数 NLP 的任务或对多数的语音相关的任务而言,往往为这些任务定制化模型,你会得到更好的结果
Seq2seq model 是一个很 powerful 的 model,它是一个很有用的 model,我们现在就是来学怎么做 seq2seq 这件事情,一般的 Seq2seq model 会分成两个部分,一部分是 Encoder 另外一部分是 Decoder,你的 input sequence 由 Encoder 处理然后将处理好的结果丢给 Decoder,由 Decoder 决定它要输出什么样的 sequence,等下我们会细讲 Encoder 和 Decoder 的内部架构
2.2 Encoder
接下来我们就来讲 Encoder 部分,那 Seq2seq model Encoder 要做的事情就是给一排向量输出另外一排向量,很多模型都可以做到,比如 self-attention、RNN、CNN,那在 Transformer 里面的 Encoder 用的就是 self-attention
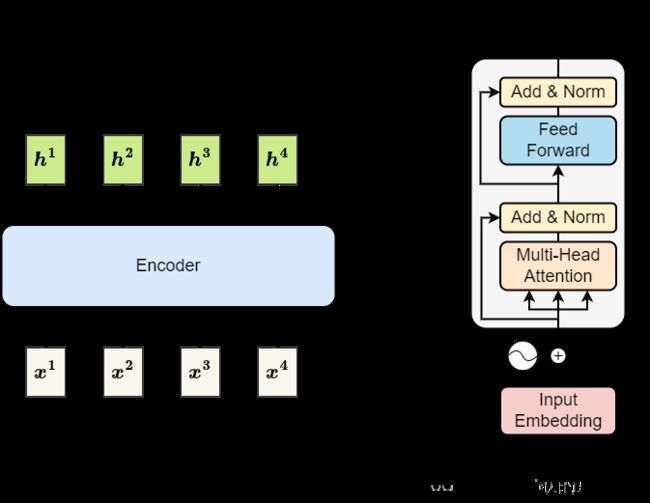
我们用一张简单的图来说明 Encoder 如 图2-4,现在的 Encoder 里面会分成很多很多的 block,每个 block 都是输入一排向量输出一排向量,每一个 block 并不是 neural network 一层,而是好几个 layer 在做的事情。在 Transformer 的 Encoder 里面每个 block 做的事情如 图2-4 所示
input 一个 sequence 之后,经过一个 self-attention 考虑整个 sequence 的信息,output 另外一排 vector,接下来会再丢到 Fully-Connected 的 feed forward network 里面,再 output 另外一排 vector,而这排 vector 就是 block 的输出。
在原来的 Transformer 里面它做的事情是更复杂的,如 图2-5 所示,在 Transformer 里面加入了一个设计,我们将 input vector 经过 self-attention 后不只是输出这个 vector,我们还要把这个 vector 加上它的 input 得到新的 output。这样子的 network 架构叫做 residual connection,那么得到 residual 的结构之后呢,再做一件事情叫做 normalization,这边用的不是 batch normalization 而是 layer normalization
layer normalization 比 batch normalization 更加简单,它不用考虑 batch 的信息,输入一个向量,输出一个向量,首先它会对同一个 feature 同一个样本中不同的 dimension 去计算 mean 和 std,然后做一个 norm 就行
得到 normlization 的输出以后输入 FC network,在 FC network 这边同样也有 residual 的结构,最后将 residual 的结果再经过一次 layer normalization 后才是 Transformer 里面 Encoder 的输出
Transformer paper 中的 Encoder 如 图2-6 所示,整个结构就是我们刚刚讲解的部分,在 input 的地方有加上 Positional Encoding 获取位置的信息,然后有一个 Multi-Head Attention,这个就是 self-attention 的 block,Add & Norm 就是 Residual 加上 Layer norm,这个复杂的 block 在 BERT 中有使用到,BERT 就是 Transformer Encoder
学到这里,你可能有许多困惑,那为什么 Encoder 要这样设计呢?不这样设计行不行呢?
行!!!不一定要这样设计,这个 Encoder network 架构的设计方式是按照原始论文来讲的,但原始论文的设计不代表它是最好的
To Learn more…
- On Layer Normalization in the Transformer Architecture
- PowerNorm: Rethinking Batch Normalization in Transformers
2.3 AT Decoder
Decoder 有两种分别是 Autoregressive Decoder 和 Non-Autoregressive Decoder
Autoregresive Decoder 是怎么运作的呢?我们拿语音辨识任务为例讲解,语音辨识的流程如 图2-7 所示,语音辨识就是输入一段声音输出一段文字,输入的声音信号经过 Encoder 之后输出一排 vector,然后送入到 Decoder 中产生语音辨识的结果。
那 Decoder 怎么产生这个语音辨识的结果呢?那首先你要给它一个特殊的符号,这个特殊的符号代表开始,Decoder 吃到 START 之后呢会吐出一个向量,这个 vector 的长度和 Vocabulary Size 一样长,向量中的每一个 row 即每一个中文字都会对应到一个数值,经过 softmax 之后这个向量的数值就对应一个分布,其总和为 1,那么分数最高的那个中文字就是最终的输出。
接下来你把 Decoder 第一次的输出 机 当做是 Decoder 新的 input,除了 START 特殊符号外还有 机 作为输入,根据这两个输入 Decoder 就会得到一个输出 器,接下来继续把 器 当做是 Decoder 新的输入,Decoder 根据三个输入输出得到 学,依此类推最终得到语音辨识的结果 机器学习,如 图2-8 所示
那这边有一个关键的地方用红色的虚线把它标出来,也就是说 Decoder 看到的输入是它在前一个时间点自己的输出,Decoder 会把自己的输出当做接下来的输入,所以当我们的 Decoder 在产生一个句子的时候,它其实有可能看到错误的东西,比如它把 器 辨识错成天气的 气,那接下来 Decoder 看到错误的辨识结果,它还是要想办法根据错误的辨识结果产生期待是正确的输出
让 Decoder 产生错误的输出,然后再被 Decoder 自己吃进去会不会造成问题呢?会不会造成 Error Propagation 的问题呢?这是有可能的,所以我们需要在 training model 的时候给 Decoder 输入一些错误的东西,这在 training 部分的时候会讲到
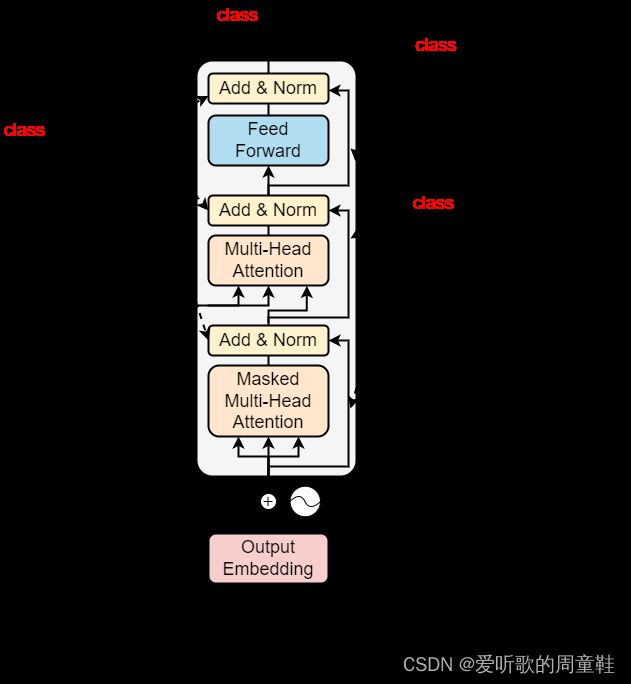
那我们接下来看下 Decoder 内部的结构,如 图2-10 所示
我们对比下 Encoder 和 Decoder,如果我们将中间部分遮挡起来,Encoder 和 Decoder 其实也没有太大的区别,这边有个稍微不一样的地方,在 Decoder 这边 Multi-Head Attention 这个 block 上面还加了一个 Maksed
原本的 self-attention 中 input 一排 vector 然后 output 另外一排 vector,每一个输出的 vector 都要看过完整的 input 以后才做决定。所以输出 b 1 \boldsymbol b^{\boldsymbol 1} b1 的时候其实是根据 a 1 \boldsymbol a^{\boldsymbol 1} a1 到 a 4 \boldsymbol a^{\boldsymbol 4} a4 所有的信息。
当我们将 self-attention 转成 Masked self-attention 以后,它的不同点在哪里呢?它的不同点是现在我们不能再看右边的部分,也就是产生 b 1 \boldsymbol b^{\boldsymbol 1} b1 的时候我们只能考虑 a 1 \boldsymbol a^{\boldsymbol 1} a1 的信息,你不能够再考虑 a 2 \boldsymbol a^{\boldsymbol 2} a2 a 3 \boldsymbol a^{\boldsymbol 3} a3 a 4 \boldsymbol a^{\boldsymbol 4} a4 同理产生 b 2 \boldsymbol b^{\boldsymbol 2} b2 的时候我们只能考虑 a 1 \boldsymbol a^{\boldsymbol 1} a1 a 2 \boldsymbol a^{\boldsymbol 2} a2 的信息,你不能够再考虑 a 3 \boldsymbol a^{\boldsymbol 3} a3 a 4 \boldsymbol a^{\boldsymbol 4} a4 依此类推,这个就是 Masked self-attention,如 图2-12 所示
讲得更具体一点,你做的事情是这样,当我们要产生 b 2 \boldsymbol b^{\boldsymbol 2} b2 的时候,我们只拿第二个位置的 Query 去和第一个位置的 Key 和第二个位置的 Key 去计算 Attention,第三个位置跟第四个位置就不管它,不去计算 Attention
那为什么需要加 Masked 呢?这件事情其实非常的直觉,回顾下 Decoder 的运作方式是一个一个的输出,它的输出是一个一个产生的,所以说是先有 a 1 \boldsymbol a^{\boldsymbol 1} a1 再有 a 2 \boldsymbol a^{\boldsymbol 2} a2 再有 a 3 \boldsymbol a^{\boldsymbol 3} a3 再有 a 4 \boldsymbol a^{\boldsymbol 4} a4,这跟原来的 self-attention 不一样,原来的 self-attention 的 a 1 \boldsymbol a^{\boldsymbol 1} a1 到 a 4 \boldsymbol a^{\boldsymbol 4} a4 是一整个输进你的 model 里面的,我们在讲 Encoder 的时候,Encoder 是一次性把 a 1 \boldsymbol a^{\boldsymbol 1} a1 到 a 4 \boldsymbol a^{\boldsymbol 4} a4 读进去,但是对 Decoder 而言先有 a 1 \boldsymbol a^{\boldsymbol 1} a1 才有 a 2 \boldsymbol a^{\boldsymbol 2} a2 才有 a 3 \boldsymbol a^{\boldsymbol 3} a3 才有 a 4 \boldsymbol a^{\boldsymbol 4} a4,所以实际上当你有 a 2 \boldsymbol a^{\boldsymbol 2} a2 要计算 b 2 \boldsymbol b^{\boldsymbol 2} b2 的时候你是没有 a 3 \boldsymbol a^{\boldsymbol 3} a3 跟 a 4 \boldsymbol a^{\boldsymbol 4} a4 的,所以你根本就没有办法把 a 3 \boldsymbol a^{\boldsymbol 3} a3 a 4 \boldsymbol a^{\boldsymbol 4} a4 考虑进来,所以在原始 Transformer 的 paper 中强调说 Decoder 的 Self-attention 是一个带有 Masked 的 Self-Attention
好,到此为止我们讲了 Decoder 的运作方式,但是这边还有一个非常关键的问题,那就是 Decoder 必须自己决定输出的 Sequence 的长度,可是到底输出的 Sequence 的长度是多少呢?我们并不知道
但是我们期待模型可以自己学习到,今天给它一个 Input Sequence 的时候 ouput sequence 应该要多长,但在我们目前的这整个 Decoder 的运作机制里面模型并不知道它什么时候应该停下来,那怎么让模型停下来呢?
我们要准备一个特殊的符号 结束,这样 Decoder 它就可以输出 结束 这个符号,如 图2-14 所示
我们期待说当 Decoder 产生完 习 以后,再把 习 当作 Decoder 的输入以后,Decoder 就要能够输出 结束 如 图2-15 所示,那整个 Decoder 产生 Sequence 的过程就结束了,如 图2-15 所示
以上就是 Autoregressive(AT) 的 Decoder 它运作的方式
2.4 NAT Decoder
接下来我们简短的说一下 Non-Autoregressive(NAT) Model 的 Decoder 运作过程,NAT Decoder 不像 AT Decoder 一次产生一个字,它是一次把整个句子都产生出来,那怎么一次性把整个句子都产生出来呢?NAT 的 Decoder 它可能吃的就是一整排的 START 的 Token,让它一次产生一排 Token 就结束了,它只要一个步骤就可以完成一个句子的生成
那这边你可能会问一个问题,刚才不是说不知道输出的 Sequence 长度是多少吗,那我们这边怎么知道 START 要放多少个当作 NAT Decoder 的输入呢?你可以有几个做法,第一个就是你 train 一个 Classifier,它吃 Encoder 的 input 输出是一个数字,代表 Decoder 要输出的长度,这是一种可能的做法。
另一种可能的做法就是不管三七二十一,你就给它一堆 START 的 Token,然后你再看什么地方输出的特殊符号 结束,输出 END 右边的就当做它没有输出,就结束了
NAT Decoder 的好处当然有平行化,速度快,且比较能够控制输出的长度,比如语音合成任务,那你在做语音合成的时候假设你突然想让你的系统讲快一点,那你可以把 Classifier 的 ouput 除以二,限制 NAT Decoder 的输出长度。语音合成任务是可以用 Seq2seq model 来做,最知名的是一个叫做 Tacotron 的模型,它是 AT 的 Decoder,还有另外一个模型叫做 FastSpeech,它是 NAT 的 Decoder
NAT Decoder 目前是一个热门的研究主题,虽然它表面上看起来有种种的厉害之处,尤其是平行化,但是 NAT Decoder 的性能往往都不如 AT Decoder,为什么性能不好呢?其实有一个叫做 Multi-Modality 的问题,这里就不细讲了
2.5 Cross attention
接下来我们要讲 Encoder 和 Decoder 如何进行交流的,也就是我们之前遮住的部分,它叫做 Cross attention 是连接 Encoder 和 Decoder 之间的桥梁,如 图2-17 所示
那这部分你会发现它有两个输入来自于 Encoder 的输出,那这个模组实际上是怎么运作的呢?那接下来根据 图2-18 说明一下
首先 Encoder 输入一排向量输出一排向量,我们把它叫做 a 1 \boldsymbol a^{\boldsymbol 1} a1 a 2 \boldsymbol a^{\boldsymbol 2} a2 a 3 \boldsymbol a^{\boldsymbol 3} a3,而 Decoder 会吃 START 这个 special token 经过 self-attention 得到一个向量,接下来把这个向量做一个 Transform 也就是乘上一个矩阵得到一个 Query 叫做 q \boldsymbol q q,然后 a 1 \boldsymbol a^{\boldsymbol 1} a1 a 2 \boldsymbol a^{\boldsymbol 2} a2 a 3 \boldsymbol a^{\boldsymbol 3} a3 都产生 key,得到 k 1 \boldsymbol k^{\boldsymbol 1} k1 k 2 \boldsymbol k^{\boldsymbol 2} k2 k 3 \boldsymbol k^{\boldsymbol 3} k3,那把 q \boldsymbol q q 和 k \boldsymbol k k 去计算 Attention 的分数得到 α 1 ′ \alpha'_1 α1′ α 2 ′ \alpha'_2 α2′ α 3 ′ \alpha'_3 α3′,当然你也可能会做 softmax,把它稍微做一下 normalization,接下来再把 α 1 ′ \alpha'_1 α1′ α 2 ′ \alpha'_2 α2′ α 3 ′ \alpha'_3 α3′ 乘上 v 1 \boldsymbol v^{\boldsymbol 1} v1 v 2 \boldsymbol v^{\boldsymbol 2} v2 v 3 \boldsymbol v^{\boldsymbol 3} v3 再把它 weighted sum 加起来得到 v \boldsymbol v v,这个 v \boldsymbol v v 接下来会丢到 Fully-Connected Network 做接下来的处理,那这个步骤 q \boldsymbol q q 来自于 Decoder, k \boldsymbol k k v \boldsymbol v v 来自于 Encoder,这个步骤就叫做 Cross Attention,所以 Decoder 就是凭借着产生一个 q \boldsymbol q q 去 Encoder 这边抽取信息出来当做接下来的输入,这个就是 Cross Attention 的运作过程
2.6 Training
我们已经讲了 Encoder,讲了 Decoder,讲了 Encoder 和 Decoder 怎么互动的,接下来我们简单聊聊训练的部分
现在假如我们要做一个语音辨识任务,那么首先你要有大量的训练数据,然后 train 一个 Seq2seq model 使得其最终的输出要和真实标签越接近越好,两个分布差异性越小越好,具体来说是计算你 model predict 的值和你的 Ground truth 之间的 cross entropy,然后 minimize cross entropy,当然这件事情和分类任务很像
那这边有一个事情值得我们注意,在 training 的时候 Decoder 的输入是什么?Decoder 的输入是 Ground Truth 是正确答案!!!,在训练的时候我们会给 Decoder 看正确答案,那这件事情叫做 Teacher Forcing:using the ground truth as input,那在 inference 的时候 Decoder 没有正确答案看,它有可能会看到错误的东西,那这之间有一个 Mismatch
Decoder 训练的时候看到的全部是正确答案,但在测试的时候可能会看到错误的东西,这个不一致的现象叫做 Exposure Bias,这会导致说 Decoder 看到错误的东西后继续产生错误,因为它在 train 的时候看到的都是正确答案呀,所以说会导致在 inference 的时候一步错,步步错,那么怎么解决这个问题呢?有一个可以思考的方向就是给 Decoder 的输入加一些错误的东西,没错,就这么直觉,那这招就叫做 Scheduled Sampling
那接下来我们聊聊训练过程中的一些小 Tips。首先是 Copy Mechanism 复制机制,那这个可能是 Decoder 所需要的,比如我们在做 chat-bot 聊天机器人的时候,复制对话是一个需要的技术,需要的能力,比如你对机器说 你好,我是周童鞋 那机器可能会回复你说 周童鞋你好,很高兴认识你,对机器来说它并不需要从头创造 周童鞋 这一段文字,它要学的也是是从使用者人的输入去 Copy 一些词汇当做是它的输出;或者是在做摘要的时候,你可能更需要 Copy 这样子的技能,所谓的摘要就是你要 train 一个 model,去读一篇文章然后产生这篇文章的摘要,对摘要这个任务而言,其实从文章里面复制一些信息出来可能是一个很关键的能力
其它的还有 Guided Attention、Beam Search 这里就不一一细说了
好,那以上我们就讲完了 Transformer 和种种的训练技巧
3. 实战
Transormer 实战,手写复现
参考博客:The Annotated Transformer
参考代码:https://github.com/harvardnlp/annotated-transformer/
The Annotated Transformer 在这篇文章中以逐行实现的形式介绍了 Transformer 原始论文的 注释 版本,强烈建议阅读原文!!!
更多细节可查看 Pytorch 官方实现 Pytorch Transformer 源码、Pytorch Transformer API
3.1 Prelims
导入必要的包和库
import torch
import torch.nn as nn
from torch.nn.functional import log_softmax
import copy
import math
import time
3.2 Model Architecture
Transfomer 的整体结构(图3-1)之前通过李宏毅老师的讲解已经非常清晰了,那简单来说 Transformer 由 Encoder 和 Decoder 两部分组成,Encoder 输入一个序列 x = ( x 1 , . . . , x n ) \boldsymbol x = (x_1,...,x_n) x=(x1,...,xn) 输出另一个序列 z = ( z 1 , . . . , z n ) \boldsymbol{z}=(z_1,...,z_n) z=(z1,...,zn),给定 z \boldsymbol z z Decoder 产生输出序列 y = ( y 1 , . . . , y n ) \boldsymbol y = (y_1,...,y_n) y=(y1,...,yn),值得注意的是 Decoder 在 ouput 下一个 token 的时候,会将上一时刻的输出 token 作为额外的输入
class EncoderDecoder(nn.Module):
"""
一个标准的 Encoder-Decoder 架构. 可作为其它模型的基础
"""
def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
super(EncoderDecoder, self).__init__()
self.encoder = encoder
self.decoder = decoder
self.src_embed = src_embed
self.tgt_embed = tgt_embed
self.generator = generator
def forward(self, src, tgt, src_mask, tgt_mask):
"处理带有 mask 的 src 和 target sequence"
return self.decode(self.encode(src, src_mask), src_mask, tgt, tgt_mask)
def encode(self, src, src_mask):
return self.encoder(self.src_embed(src), src_mask)
def decode(self, memory, src_mask, tgt, tgt_mask):
return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)
class Generator(nn.Module):
"定义标准 linear + softmax 步骤"
def __init__(self, d_model, vocab):
super(Generator, self).__init__()
self.proj = nn.Linear(d_model, vocab)
def forward(self, x):
return log_softmax(self.proj(x), dim=-1)
Transformer = Encoder + Decoder + Generator(Linear + log_softmax) 整体三部分组成
3.2.1 Encoder
Encoder 由 N N N 个相同 layers 堆叠而成( N = 6 N = 6 N=6)
def clones(module, N):
"产生 N 个相同的 layers"
return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])
class Encoder(nn.Module):
"Encoder 由 N 个 layers 堆叠而成"
def __init__(self, layer, N):
super(Encoder, self).__init__()
self.layers = clones(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, mask):
"将 input 和 mask 一依次通过各层"
for layer in self.layers:
x = layer(x, mask)
return self.norm(x)
那接下来我们需要在两个 sub-layer 中实现 residual connection,然后去做 layer normalization
class LayerNorm(nn.Module):
"layerborm 模块的构建"
def __init__(self, features, eps=1e-6):
super(LayerNorm, self).__init__()
self.a_2 = nn.Parameter(torch.ones(features))
self.b_2 = nn.Parameter(torch.zeros(features))
self.eps = eps
def forward(self, x):
mean = x.mean(-1, keepdim=True)
std = x.std(-1, keepdim=True)
return self.a_2 * (x - mean) / (std + self.eps) + self.b_2
每个 sub-layer 的输出是 L a y e r N o r m ( x + S u b l a y e r ( x ) ) \mathrm{LayerNorm}(x+\mathrm{Sublayer}(x)) LayerNorm(x+Sublayer(x)) 其中 S u b l a y e r ( x ) \mathrm{Sublayer}(x) Sublayer(x) 是 sub-layer 本身实现的功能,我们在每个 sub-layer 的输出上应用 dropout,然后再加上 sub-layer 的输入做 normalization
为了确保 residual connection,模型中所有的 sub-layer 以及 embedding layer 的输出维度设置为 d m o d e l = 512 d_{model} = 512 dmodel=512
class SublayerConnection(nn.Module):
"""
A residual connection(layernorm之后)
"""
def __init__(self, size, dropout):
super(SublayerConnection, self).__init__()
self.norm = LayerNorm(size)
self.dropout = nn.Dropout(dropout)
def forward(self, x, sublayer):
"residual connection 应用于任何具有相同 size 的 sublayer"
return x + self.dropout(sublayer(self.norm(x)))
每个 layer 都拥有两个 sub-layer,第一个 layer 就是一个 multi-head self-attention mechanism,第二个 layer 就是一个 position-wise fully connected feed-forward network
class EncoderLayer(nn.Module):
"Encoder 由 self-attention 和 feed forward 两部分组成"
def __init__(self, size, self_attn, feed_forward, dropout):
super(EncoderLayer, self).__init__()
self.self_attn = self_attn
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 2)
self.size = size
def forward(self, x, mask):
"参考 图3-1 左边连接"
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
return self.sublayer[1](x, self.feed_forward)
代码的各部分在 Encoder 图中的说明见 图3-2
3.2.2 Decoder
Decoder 也是由 N N N 个相同 layers 堆叠而成( N = 6 N = 6 N=6)
class Decoder(nn.Module):
"带 mask 的通用 N 层 decoder"
def __init__(self, layer, N):
super(Decoder, self).__init__()
self.layers = clones(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, memory, src_mask, tgt_mask):
for layer in self.layers:
x = layer(x, memory, src_mask, tgt_mask)
return self.norm(x)
Decoder 除了拥有 Encoder 的两个 sub-layer 之外还插入了第三个 sub-layer,也就是我们之前讲过的 Encoder 和 Decoder 之间的桥梁 Cross-attention,它也是一个 multi-head attention 不同的是它吃 Encoder 的 output,它由 Decoder 产生 q \boldsymbol q q 通过 Encoder 的 k \boldsymbol k k v \boldsymbol v v 抽取信息。与 Encoder 类似,对于 Decoder 中的每个 sub-layer 我们也需要实现 residual connection 和 layer normalization
class DecoderLayer(nn.Module):
"DecoderLayer 由 self-attention cross-attention 和 feed forward 三部分组成"
def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
super(DecoderLayer, self).__init__()
self.size = size
self.self_attn = self_attn
self.src_attn = src_attn
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 3)
def forward(self, x, memory, src_mask, tgt_mask):
"参考 图3-1 右边连接"
m = memory
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
return self.sublayer[2](x, self.feed_forward)
Masked Multi-Head Self-attention 中 mask 的创建,确保 Decoder 看到的只是前一个时刻的 output,而不去考虑后面时刻的 output
def subsequent_mask(size):
"Maks 输出后续位置"
attn_shape = (1, size, size)
subsequent_mask = torch.triu(torch.ones(attn_shape), diagonal=1).type(torch.uint8)
return subsequent_mask == 0
下面 attention mask 显示了每个 tgt word(row) 被允许看的位置(column),确保 Decoder 在 training 过程中阻断了对未来 words 的关注
代码的各部分在 Decoder 图中的说明见 图3-4
3.2.3 Attention
attention function 可以被描述为将一个 query 和 一组 key-value 映射到一个输出,其中的 query、key、value 以及 output 都是 vector,输出的计算通过 value 的 weighted sum,其中分配给每个 value 的 weight 是由 query 与相应的 key 的 compatibility function 计算的
我们把这个特别的 attention 叫做 Scaled Dot-Product Attention,它的 input 由 d k d_k dk 维度的 query、key 以及 d v d_v dv 维度的 value 组成,我们对 query 和所有的 key 计算 dot products,然后除以 d k \sqrt{d_k} dk 使用 softmax 来获得 value 上的权重,如 图3-5 所示
上述就是 self-attention 的实现过程,我们再来回顾下李宏毅老师从矩阵的角度来分析 self-attention 的整个运作过程(详细内容见 1.3 小节)
那么首先我们会对 input 拼接成矩阵 I I I 分别乘上 W q W^q Wq W k W^k Wk W v W^v Wv 三个不同的矩阵得到 Q Q Q K K K V V V 如 图3-6 所示
那么接下来每一个 q \boldsymbol q q 都会跟每一个 k \boldsymbol k k 去计算 dot product 得到 attention score,从矩阵角度分析就是矩阵 K K K 和 Q Q Q 相乘, K K K 矩阵的 row 就是 k 1 \boldsymbol k^{\boldsymbol 1} k1 到 k 4 \boldsymbol k^{\boldsymbol 4} k4, Q Q Q 矩阵的 column 就是 q 1 \boldsymbol q^{\boldsymbol 1} q1 到 q 4 \boldsymbol q^{\boldsymbol 4} q4 得到矩阵 A A A,那矩阵 A A A 存储的就是 Q Q Q 和 K K K 之间的 attention 分数
那么接下来我们会对 attention 分数做一下 normalization,对这边的每一个 column 做 softmax,使其每一个 column 的值相加为 1,如 图3-7所示
接下来,我们需要通过 attention 分数矩阵 A ′ A' A′ 计算得到输出,那输出是怎么被计算出来的呢?你就让 V V V 乘上 A ′ A' A′ 就可以了,如 图3-8所示
在实际的应用中,我们计算的输出的矩阵为:
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V \mathrm{Attention}(Q,K,V) = \mathrm{softmax}(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V)=softmax(dkQKT)V
def attention(query, key, value, mask=None, dropout=None):
"计算 'Scaled Dot Product Attention'"
d_k = query.size(-1) # query 维度
scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
if mask is not None:
# 将 mask 部分设置很大的负数,通过 softmax 后将这些得分转化为接近于零的概率
scores = scores.masked_fill(mask == 0, -1e9)
p_attn = scores.softmax(dim=-1)
if dropout is not None:
p_attn = dropout(p_attn)
return torch.matmul(p_attn, value), p_attn
最常见的两种 Attention 的计算方式是 Dot-product 和 Additive,在前面我们已经讨论过了,这边就不再赘述了(详细内容见 1.2 小节),dot-product 算法的实现与我们之前描述的一样,除了缩放系数 1 d k \frac{1}{\sqrt{d_k}} dk1 的不同。我们采用 dot-product 来实现 Attention 的计算,虽然 Dot-product 和 Additive 二者在理论上的复杂性相似,但 dot-product 在实践中要快得多,而且空间效率更高,因为它可以用高度优化的矩阵乘法代码来实现
接下来我们简单聊聊为什么在实际应用中 Dot-product 需要进行缩放
首先,当 d k d_k dk 较小时,点积算法和加性算法的表现相似,因为较小的 d k d_k dk 不会导致点积的幅度过大或过小,而加性算法也不需要额外的缩放操作
然而,当 d k d_k dk 较大时,点积算法会导致点积的幅度变大,那为什么点积的幅度会变大呢?我们可以假设 q \boldsymbol q q 和 k \boldsymbol k k 是具有均值为 0,方差为 1 的独立随机变量。点积的结果为 q ⋅ k = ∑ i = 1 d k q i k i q \cdot k =\sum_{i=1}^{d_k}q_ik_i q⋅k=∑i=1dkqiki 其均值为 0,方差为 d k d_k dk。因此,随着 d k d_k dk 的增大,点积的幅度也会增大
当点积的幅度变大时,经过 softmax 函数后,得到的 attention score 会呈现较小的梯度值,甚至接近于零。这可能会导致梯度消失或梯度爆炸的问题,使得模型的训练变得困难
为了抵消点积幅度变大带来的影响,我们将点积缩放为 1 d k \frac{1}{\sqrt{d_k}} dk1。通过缩放操作,可以确保点积的幅度不会过大,从而保持 softmax 函数在梯度较大的区域内,避免出现梯度极小的情况。
self-attention 它有一个进阶的版本叫做 Muti-head Self-attention 如 图3-9所示 它也被应用在 Transformer 当中,其计算如下:
M u l t i H e a d ( Q , K , V ) = C o n c a t ( h e a d 1 , . . . , h e a d h ) W O w h e r e h e a d i = A t t e n t i o n ( Q W i Q , K W i K , V W i V ) \mathrm{MultiHead}(Q,K,V) = \mathrm{Concat}(\mathrm{head_1},...,\mathrm{head_h})W^O \\ \mathrm{where}\ \mathrm{head_i} = \mathrm{Attention}(QW_i^Q,KW_i^K,VW_i^V) MultiHead(Q,K,V)=Concat(head1,...,headh)WOwhere headi=Attention(QWiQ,KWiK,VWiV)
其中参数矩阵 W i Q ∈ R d m o d e l × d k W_i^Q\in\mathbb{R}^{d_\mathrm{model}\times d_k} WiQ∈Rdmodel×dk W i K ∈ R d m o d e l × d k W_i^K\in\mathbb{R}^{d_{\mathrm{model}}\times d_k} WiK∈Rdmodel×dk W i V ∈ R d m o d e l × d v W_i^V\in\mathbb{R}^{d_{\mathrm{model}}\times d_v} WiV∈Rdmodel×dv W O ∈ R h d v × d m o d e l W^O\in\mathbb{R}^{hd_v \times d_{\mathrm{model}}} WO∈Rhdv×dmodel
在接下来的应用中,我们试用 h = 8 h = 8 h=8 代表 8 头注意力, d k = d v = d m o d e l / h = 64 d_k = d_v = d_{\mathrm{model}}/h = 64 dk=dv=dmodel/h=64
class MultiHeadedAttention(nn.Module):
def __init__(self, h, d_model, dropout=0.1):
""
super(MultiHeadedAttention, self).__init__()
assert d_model % h == 0 # 断言
# 我们假设 d_v 总等于 d_k
self.d_k = d_model // h
self.h = h
self.linears = clones(nn.Linear(d_model, d_model), 4)
self.attn = None
self.dropout = nn.Dropout(p=dropout)
def forward(self, query, key, value, mask=None):
"图3-9的实现"
if mask is not None:
# 同样的 mask 应用到所有的 head 中
mask = mask.unsqueeze(1)
nbatches = query.size(0)
# 1) 线性变换 d_model => h x d_k
query, key, value = [
lin(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
for lin, x in zip(self.linears, (query, key, value))
]
# 2) 根据变换后的 vector 计算 attention score
x, self.attn = attention(
query, key, value, mask=mask, dropout=self.dropout
)
# 3) Concat
x = (
x.transpose(1, 2)
.contiguous()
.view(nbatches, -1, self.h * self.d_k)
)
del query
del key
del value
return self.linears[-1](x)
我们来对下面的输入变换代码进行分析:
query, key, value = [
lin(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
for lin, x in zip(self.linears, (query, key, value))
]
这段代码具体做了什么工作呢?它主要是将输入进来的 query、key、value 进行线性变换并投影,进行一些维度变换的操作,目的是将输入数据调整为适合多头注意力机制的形式,它干的活应该是 图3-10 红色框中的内容
我们再来对多头注意力拼接代码进行分析:
x = (
x.transpose(1, 2)
.contiguous()
.view(nbatches, -1, self.h * self.d_k)
)
在上述示例代码中,多头注意力的拼接是通过维度变换来实现的,x 是经过注意力计算后的结果,维度为 (nbatches, h, seq_len, d_k),其中 nbatches 表示批次大小,h 表示头部的数量,seq_len 表示序列长度,d_k 表示每个头部的维度。
首先,通过 transpose 函数进行维度变换,将维度 (nbatches, h, seq_len, d_k) 转置为 (nbatches, seq_len, h, d_k),这是为了将每个头部的注意力计算结果放在相邻维度上。
然后,通过 contiguous 函数确保数据在内存中是连续的,以便进行后续的视图变换。
最后,通过 view 函数将结果的形状从 (nbatches, seq_len, h, d_k) 调整为 (nbatches, seq_len, h * d_k),即将所有头部的注意力结果沿最后一个维度拼接起来。
3.2.4 Position-wise Feed-Forward Networks
在 Encoder 和 Decoder 当中除了 attention 层还包含 fully connected feed-forward network,
它包含如下两个线性变换吗,中间有一个 ReLU 激活
F F N ( x ) = max ( 0 , x W 1 + b 1 ) W 2 + b 2 \mathrm{FFN}(x)=\max(0,xW_1+b_1)W_2+b_2 FFN(x)=max(0,xW1+b1)W2+b2
可以把它当做两个 kernel size 等于 1 的卷积操作,输入和输出维度是 d m o d e l = 512 d_{\mathrm{model}}=512 dmodel=512 中间层维度是 d f f = 2048 d_{ff} = 2048 dff=2048
class PositionwiseFeedForward(nn.Module):
"FFN(feed-forward network) 的实现"
def __init__(self, d_model, d_ff, dropout=0.1):
super(PositionwiseFeedForward, self).__init__()
self.w_1 = nn.Linear(d_model, d_ff)
self.w_2 = nn.Linear(d_ff, d_model)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
return self.w_2(self.dropout(self.w_1(x).relu()))
3.2.5 Embeddings and Softmax
与其他 Seq2seq model 类似,在 Transformer 中我们使用 embeddings 将输入 tokens 和 输出 tokens 转换为 d m o d e l d_{\mathrm{model}} dmodel 维度的 vectors,我们还使用线性层和 softmax 将 Decoder 的输出转换为预测 next-token 的概率
在 Transformer 中我们在 Encoder 和 Decoder 的两个 Embedding 层以及预测 softmax 之前的线性变换层之间共享相同的权重矩阵,并将权重乘以 d m o d e l \sqrt{d_{\mathrm{model}}} dmodel 进行缩放,以便使嵌入向量的数值范围更合适
具体来说,对于编码器和解码器的嵌入层,它们都使用相同的权重矩阵将输入的 token 索引转换为嵌入向量。这意味着编码器和解码器共享相同的词嵌入表示,从而使它们能够更好地理解和处理相同的词汇。(from chatGPT)
另外,在预测 softmax 之前的线性变换层中,也使用了相同的权重矩阵。这一层的作用是将解码器的输出转换为预测下一个 token 的概率分布。通过共享权重矩阵,可以使编码器和解码器之间的转换更加一致和连贯,从而提升模型的性能和泛化能力。
class Embeddings(nn.Module):
def __init__(self, d_model, vocab):
super(Embeddings, self).__init__()
self.lut = nn.Embedding(vocab, d_model)
self.d_model = d_model
def forward(self, x):
return self.lut(x) * math.sqrt(self.d_model)
3.2.6 Positional Encoding
由于 Transformer 中不包含递归和卷积,为了使模型能够利用序列的顺序,我们必须添加一些关于序列中 tokens 的相对或绝对位置的信息,为此,我们在 Encoder 和 Decoder 的底部为 input embeddings 添加 “位置编码”,这些位置编码的拥有相同的维度 d m o d e l d_{\mathrm{model}} dmodel,这使得二者可以相加(详细内容见 1.5 小节)
当然有许多关于 positional encoding 的实现啦,那我们可以使用不同频率的 sine 和 cosine 函数来实现:
P E ( p o s , 2 i ) = sin ( p o s / 1000 0 2 i / d m o d e l ) P E ( p o s , 2 i + 1 ) = cos ( p o s / 1000 0 2 i / d m o d e l ) PE_{(pos,2i)} = \sin(pos/10000^{2i/d_{\mathrm{model}}}) \\ PE_{(pos,2i+1)} = \cos(pos/10000^{2i/d_{\mathrm{model}}}) PE(pos,2i)=sin(pos/100002i/dmodel)PE(pos,2i+1)=cos(pos/100002i/dmodel)
其中 p o s pos pos 代表位置, i i i 代表维度,也就是说,位置编码的每个维度都对应着一个正弦波,波长形成一个几何级数,从 2 π 2\pi 2π 到 10000 ⋅ 2 π 10000 \cdot 2\pi 10000⋅2π 我们之所以选择这个函数,是因为我们假设它能让模型轻易地学会通过相对位置来注意,因为对于任何固定的偏移量 k k k 来说, P E p o s + k PE_{pos+k} PEpos+k 都可以表示为一个线性函数 P E p o s PE_{pos} PEpos
除此之外,我们对 Encoder 和 Decoder 的 embedding 和 positional encoding 总和进行了 dropout,且 P d r o p = 0.1 P_{drop} = 0.1 Pdrop=0.1
class PositionalEncoding(nn.Module):
"位置编码实现"
def __init__(self, d_model, dropout, max_len=5000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
# 在对数空间中计算一次位置编码
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1) # [5000,1]
div_term = torch.exp(
torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model)
)
# 从第 0 维度开始,每隔 2 个维度进行切片
pe[:, 0::2] = torch.sin(position * div_term)
# 从第 1 维度开始,每隔 2 个维度进行切片
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0) # [1,5000,512]
self.register_buffer("pe", pe)
def forward(self, x):
x = x + self.pe[:, : x.size(1)].requires_grad_(False)
return self.dropout(x)
位置编码的部分代码如下:
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1) # [5000,1]
div_term = torch.exp(
torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model)
)
# 从第 0 维度开始,每隔 2 个维度进行切片
pe[:, 0::2] = torch.sin(position * div_term)
# 从第 1 维度开始,每隔 2 个维度进行切片
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0) # [1,5000,512]
在上述代码中,div_term 的计算方式是使用了自然对数的形式,通过 torch.exp() 函数来进行指数运算,而不是直接计算 10000^{2i/d_model}。这样的目的是为了避免指数运算中可能出现的数值溢出或下溢问题。
同时位置编码向量是交替使用正弦和余弦函数,具体来说,假设 d_model 为 512,那么位置编码的维度就是 512。在这 512 个维度中,奇数维度对应的位置编码使用正弦函数生成,偶数维度对应的位置编码使用余弦函数生成。这样做的目的是让相邻位置之间的向量表示具有不同的性质,以便于模型更好地捕捉到词序列的顺序和位置关系。如 图3-11 所示
3.2.7 Full Model
定义一个函数来构建一个完整的 model
def make_model(
src_vocab, tgt_vocab, N=6, d_model=512, d_ff=2048, h=8, dropout=0.1
):
"从超参数中构建模型"
c = copy.deepcopy
attn = MultiHeadedAttention(h, d_model)
ff = PositionwiseFeedForward(d_model, d_ff, dropout)
position = PositionalEncoding(d_model, dropout)
model = EncoderDecoder(
Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
Decoder(DecoderLayer(d_model, c(attn), c(attn), c(ff), dropout), N),
nn.Sequential(Embeddings(d_model, src_vocab), c(position)),
nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)),
Generator(d_model, tgt_vocab),
)
# 非常重要的步骤
# 使用 Glorot / fan_avg 初始化参数
for p in model.parameters():
if p.dim() > 1:
nn.init.xavier_uniform_(p)
return model
3.2.8 Inference
我们通过模型的前向传播来做预测,当然由于模型还没有被训练,其输出都是随机产生的。接下来,我们将构建 Loss function,并尝试训练我们的模型来记忆从 1 到 10 的数字
def inference_test():
test_model = make_model(11, 11, 2)
test_model.eval()
src = torch.LongTensor([[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]])
src_mask = torch.ones(1, 1, 10)
memory = test_model.encode(src, src_mask)
ys = torch.zeros(1, 1).type_as(src)
for i in range(9):
out = test_model.decode(
memory, src_mask, ys, subsequent_mask(ys.size(1)).type_as(src.data)
)
prob = test_model.generator(out[:, -1])
_, next_word = torch.max(prob, dim=1)
next_word = next_word.data[0]
ys = torch.cat(
[ys, torch.empty(1, 1).type_as(src.data).fill_(next_word)], dim=1
)
print("Example Untrained Model Prediction:", ys)
def run_tests():
for _ in range(10):
inference_test()
run_tests()
输出如下:
Example Untrained Model Prediction: tensor([[ 0, 6, 2, 3, 10, 10, 1, 1, 1, 1]])
Example Untrained Model Prediction: tensor([[0, 1, 3, 0, 1, 0, 1, 0, 1, 3]])
Example Untrained Model Prediction: tensor([[ 0, 4, 2, 9, 3, 10, 6, 9, 3, 10]])
Example Untrained Model Prediction: tensor([[0, 0, 0, 0, 2, 2, 2, 2, 2, 2]])
Example Untrained Model Prediction: tensor([[0, 2, 2, 2, 2, 3, 2, 2, 3, 3]])
Example Untrained Model Prediction: tensor([[ 0, 4, 8, 3, 7, 10, 3, 2, 2, 2]])
Example Untrained Model Prediction: tensor([[0, 5, 0, 2, 5, 0, 2, 5, 0, 2]])
Example Untrained Model Prediction: tensor([[0, 7, 9, 4, 3, 3, 3, 9, 4, 5]])
Example Untrained Model Prediction: tensor([[0, 6, 6, 6, 6, 6, 6, 6, 6, 6]])
Example Untrained Model Prediction: tensor([[0, 5, 5, 5, 5, 5, 5, 5, 5, 5]])
至此,模型的网络结构已经搭建完毕,接下来我们简单聊聊模型训练的部分内容
3.3 Model Training
在本节我们只介绍模型训练过程中的一些细节,详细内容请查看原文
我们稍作停顿,先介绍下训练 Transformer Model 所需要的一些工具,首先,我们定义了一个 Batch 对象,用于保存训练用的 src 和 target 句子以及对应的 mask
3.3.1 Batches and Masking
class Batch:
"""在训练时用于保存带 mask 的数据对象."""
def __init__(self, src, tgt=None, pad=2):
self.src = src
self.src_mask = (src != pad).unsqueeze(-2)
if tgt is not None:
self.tgt = tgt[:, :-1]
self.tgt_y = tgt[:, 1:]
self.tgt_mask = self.make_std_mask(self.tgt, pad)
self.ntokens = (self.tgt_y != pad).data.sum()
@staticmethod
def make_std_mask(tgt, pad):
"Create a mask to hide padding and future words"
tgt_mask = (tgt != pad).unsqueeze(-2)
tgt_mask = tgt_mask & subsequent_mask(tgt.size(-1)).type_as(
tgt_mask.data
)
return tgt_mask
在上面的示例代码中 src_mask 为输入掩码张量,通过将 src 中等于 pad 的元素设置为 False 而生成,src_mask 的作用是屏蔽 input sequence 中的 padding token,确保 model 不会在填充部分产生任何注意力。在 Transformer 模型中,padding token 通常用来对齐不同长度的句子,以便进行批处理训练。通过在 src_mask 中将填充标记所在的位置设置为 False,模型在计算注意力时会忽略这些填充部分。
比如你的 input sequence 是 机器学习,而你的输入序列中有固定的最大长度,比如 512,则 model 需要将其填充到与最大长度相同的维度。填充的部分可以使用特定的填充标记(例如 pad = 2)来表示,然后在 src_mask 中将这些填充位置的值设置为 False,以确保模型不会关注到填充的部分
需要注意的是,填充操作通常是在数据预处理阶段完成的,而 src_mask 的生成是在模型训练过程中进行的,目的是在每个批次中动态地生成掩码,以适应不同长度的输入序列。
self.tgt 表示 Decoder 的输入,去除了最后一个 token,也就是 图3-12 中的红色框内容,即 START 机 器 学,它是需要计算 mask 的,不能让 Decoder 看到未来的结果
对于 tat_mask,在 Decoder 中,除了像 src_mask 遮挡填充标记之外,还需要屏蔽后续位置的信息,因此它还需要通过 subsequent_mask 函数生成一个遮罩,将后续位置的信息屏蔽掉
self.tgt_y 表示的是 机 器 学 习,它是用来计算非填充标记数量 self.ntokens 的,它不需要计算掩码
那接下来,我们将创建一个训练状态对象用于跟踪训练过程中的一些信息
3.3.2 Training Loop
class TrainState:
"""跟踪 number of steps, example, and tokens processed"""
step: int = 0 # Steps in the current epoch
accum_step: int = 0 # Number of gradient accumulation steps
samples: int = 0 # total # of examples used
tokens: int = 0 # total # of tokens processed
def run_epoch(
data_iter,
model,
loss_compute,
optimizer,
scheduler,
mode="train",
accum_iter=1,
train_state=TrainState()
):
"Train a single epoch"
start = time.time()
total_tokens = 0
total_loss = 0
tokens = 0
n_accum = 0
for i, batch in enumerate(data_iter):
out = model.forward(
batch.src, batch.tgt, batch.src_mask, batch.tgt_mask
)
loss, loss_node = loss_compute(out, batch.tgt_y, batch.ntokens)
# loss_node = loss_node / accum_iter
if mode == "train" or mode == "train+log":
loss_node.backward()
train_state.step += 1
train_state.samples += batch.src.shape[0]
train_state.tokens += batch.ntokens
if i % accum_iter == 0:
optimizer.step()
optimizer.zero_grad(set_to_none=True)
n_accum += 1
train_state.accum_step += 1
scheduler.step()
total_loss += loss
total_tokens += batch.ntokens
tokens += batch.ntokens
if i % 40 == 1 and (mode == "train" or mode == "train+log"):
lr = optimizer.param_groups[0]["lr"]
elapsed = time.time() - start
print(
(
"Epoch Step: %6d | Accumulation Step: %3d | Loss: %6.2f "
+ "| Tokens / Sec: %7.1f | Learning Rate: %6.1e"
)
% (i, n_accum, loss / batch.ntokens, tokens / elapsed, lr)
)
start = time.time()
tokens = 0
del loss
del loss_node
return total_loss / total_tokens, train_state
3.3.3 Optimizer
Adam optimizer β 1 = 0.9 \beta_1 = 0.9 β1=0.9 β 2 = 0.98 \beta_2 = 0.98 β2=0.98 ϵ = 1 0 − 9 \epsilon = 10^{-9} ϵ=10−9
学习率按照如下公式更新:
l r a t e = d m o d e l − 0.5 ⋅ min ( s t e p _ n u m − 0.5 , s t e p _ n u m ⋅ w a r m u p _ s t e p s − 1.5 ) lrate = d_{\mathrm{model}}^{-0.5} \cdot \min(step\_num^{-0.5},step\_num \cdot warmup\_steps^{-1.5}) lrate=dmodel−0.5⋅min(step_num−0.5,step_num⋅warmup_steps−1.5)
其中 w a r m u p _ s t e p s = 4000 warmup\_steps = 4000 warmup_steps=4000
注意:这部分非常重要,需要用该设置去训练模型
def rate(step, model_size, factor, warmup):
"""
we have to default the step to 1 for LambdaLR function
to avoid zero raising to negative power
"""
if step == 0:
step == 1
return factor * (
model_size ** (-0.5) * min(step ** (-0.5), step * warmup ** (-1.5))
)
3.3.4 Regularization
Label Smoothing 值 ϵ l s = 0.1 \epsilon_{ls} = 0.1 ϵls=0.1 采用 KL dive loss 而不采用 one-hot target distribution
class LabelSmoothing(nn.Module):
"Implement label smoothing"
def __init__(self, size, padding_idx, smoothing=0.0):
super(LabelSmoothing, self).__init__()
self.criterion = nn.KLDivLoss(reduction="sum")
self.padding_idx = padding_idx
self.confidence = 1.0 - smoothing
self.smoothing = smoothing
self.size = size
self.true_dist = None
def forward(self, x, target):
assert x.size(1) == self.size
true_dist = x.data.clone()
true_dist.fill_(self.smoothing / (self.size - 2)) # 减 2 包含 START 和 END token
# 将 target 中每个元素的索引位置对应的 true_dist 中的值替换为 self.confidence
true_dist.scatter_(1, target.data.unsqueeze(1), self.confidence)
true_dist[:, self.padding_idx] = 0
mask = torch.nonzero(target.data == self.padding_idx)
if mask.dim() > 0:
true_dist.index_fill_(0, mask.squeeze(), 0.0)
self.true_dist = true_dist
return self.criterion(x, true_dist.clone().detach())
我们在计算 Loss 的时候使用的是 KL 散度损失函数而不是传统的交叉熵损失函数,在 LabelSmoothing 类中,KL 散度损失函数 self.criterion 的输入是模型的输出 x 和真实标签平滑后的分布 true_dist
至此,Transformer 的实战部分告一段落了,后续实际数据的训练可自行查看相关内容,博主这边只介绍一些细节实现内容
3.4 实战总结
由于博主对 NLP 相关的任务不了解,因此刚开始的时候一头雾水,只能跟随参考博客依葫芦画瓢,不过后续根据 Transformer 的网络结构,回顾李宏毅老师讲解的课程之后,也慢慢开始熟悉起来
先从网络结构方面入手,Transformer 模型分为 Encoder + Decoder 两部分,参考博客是将 Decoder 部分的 Linear + softmax 部分单独构建了一个 Generator 类,在 Encoder 和 Decoder 中都有 residual connect,主要是通过类 SublayerConnection 来实现,里面实现了 Layernorm + sublayer + dropout,而 sublayer 在 Encoder 中主要是 Multi-Head Attention 和 Fully Connected Feed-Forward Network,在 Decoder 当中也差不多,只是 Multi-Head Attention 带有 mask
整个网络结构的搭建 Multi-Head Attenion 部分有难度,不过结合李宏毅老师的矩阵角度理解还是比较容易实现的,除此之外,还有 positional encoding 部分也值得注意,这次实现主要是通过采用不同频率的正弦余弦函数来实现位置编码
在模型训练部分也有一些细节值得我们关注,首先是 mask 的生成,tgt_mask 的生成要考虑到不能让 Decoder 看到后续位置的信息,因此与 src_mask 的生成略有不同,此外,为了让减轻模型对训练数据中的噪声和过拟合的敏感性,采用了标签平滑的分布代替传统的 one-hot 编码的目标分布,同时采用 KL 散度损失函数来度量模型输出与平滑后的分布之间的差异性
总的来说我们可以根据网络结构图把握总体方向,一些细枝末节可以问问 chatGPT
总结
博主之前一直对 NLP 相关的内容不感冒,对于 Transformer 也早有听闻,不过始终没有找到一个适合博主的讲解,这次乘着要学习 BEVFormer 补了下 Transformer 的相关知识,通过听了李宏毅老师非常通俗的讲解后,对 Transformer 有了一个整体的了解。
简单来说,Transformer 是一个 Seq2seq model,它由 Encoder、Decoder 以及桥梁 Cross attention 三部分组成,其中 Encoder 用到的就是 Self-attention,而 Decoder 和 Encoder 非常相像,不过使用的是带有 Masked 的 Multi-Head Attention,桥梁 Cross attention 借助 Decoder 产生的 q \boldsymbol q q 通过 Encoder 的 k \boldsymbol k k v \boldsymbol v v 抽取信息当做下一步的输入
简单了解了 Transformer 对后续学习 BEVFormer 有一个基础,同时对 NLP ASR 相关的任务也产生了一定的兴趣,非常感谢李宏毅老师!!!