Polygon zkEVM PIL技术文档
1. 引言
Polygon zkEVM中引入了Polynomial Identity Language (PIL),定位为:可验证计算的机器描述语言。
PIL为定义eAIR约束的领域特定语言(domain-specific language, DSL)。创建PIL的目的是为开发者提供一套整体框架,是开发者可通过简单易用的接口来构建程序,以及对证明机制的复杂性进行抽象。
PIL的主要特点为模块化,允许:
- 开发者从更大的程序中实例化 定义名为namespace的参数化程序。
以模块化方式来构建(大而复杂的)程序,使得程序更易于测试、审查、审计以及形式化验证。通过使用PIL,开发者可创建其自定义的namespace,或根据某些公共库实例化的namespace。
许多DSL或工具栈,如Circom或Halo2,都专注于对某种特殊计算模式(如算术电路arithmetic circuit)的抽象。但是近期的如STARKs等证明系统表明,算术电路并不是对所有用户场景的最优计算模式。已知某完整的编程语言,为某circuit satisfiability problem计算有效性证明,由于复用逻辑的开销,可能会导致长的证明时间。以底层编程语言来开发程序,可实现更短的证明时长——如PIL这种证明/验证辅助语言。
2. PIL简单示例
PIL简单示例:
- 设计一个名为Multiplier的PIL程序:计算2个整数的乘积
可用3个多项式来对该程序建模,其中:
- 2个多项式 freeIn 1 , freeIn 2 \text{freeIn}_1,\text{freeIn}_2 freeIn1,freeIn2分别对应2个输入
- 1个多项式 out \text{out} out对应输出
当且仅当如下identity成立时,该程序是计算正确的:
out = freeIn 1 ⋅ freeIn 2 \text{out}=\text{freeIn}_1\cdot \text{freeIn}_2 out=freeIn1⋅freeIn2
Multiplier程序的某个正确execution trace如下图所示:
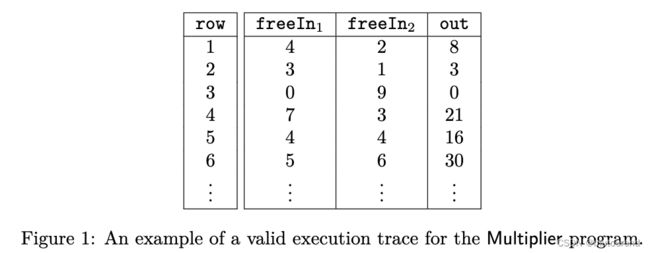
上图中的每一行都满足该identity,即意味着out列中均为正确值。其中的i输入列和输出列可做如下分类:
- Free Input多项式:这些列用于为某计算引入各种输入。称其为“free”是因为在计算的每个周期中,这些值不严格依赖于任何之前的迭代。这些类似于整个计算中的独立变量。
- State变量:为包含了程序状态的列。此处是指表示程序在每个step输出值的集合。如若在最后一个step,即表示整个计算的输出值的集合。
- 关键字namespace:用于框定程序定义范围。在namespace内,可定义程序所需的多项式,以及这些多项式间应满足的约束关系。
namespace应实例化为:- 唯一名称(如Multiplier)
- + 表示程序长度(即该程序任意execution trace的行数)的参数(如2**10)
- 关键字commit:表示相应的多项式为committed多项式。
从证明角度看,committed多项式仅对Prover已知,对Verifier是未知的。 - 关键字constant:表示在同一程序的任意执行中,这些值都不可改变。
即常量多项式为计算本身所固有的。从证明角度来看,常量多项式对所有参与方(Prover和Verifier)都是公开已知的。
不过很容易发现上述Multiplier程序的设计是不唯一的。随着输入的增加,committed多项式也会增加,如需要计算 2 10 2^{10} 210个输入的乘积,则需要设计 2 10 2^{10} 210个committed多项式,这是不切实际的。
不过,接下来的设计策略,通过引入另一个多项式来标记每次运算的起始行,可将 2 10 2^{10} 210个committed多项式 reduce为 一个,然后再加一个多项式来维护运算结果,即一共仅需要3列,就可以计算 2 10 2^{10} 210个输入的乘积。

如上图所示:
- 对于相同的总行数,该设计所能检查的乘法数量要 少于 图1设计。图1设计中每行可检查一个乘法运算,而图2中的乘法数量得减半。
- 引入名为RESET的constant多项式:其在奇数行为1,偶数行为0。
可发现:- 当RESET为1时,out多项式的值为freeIn多项式前2个值的乘积。
- 当RESET为0时(即中间step),out多项式中存储该乘积运算的第一个输入。
- 为反映out多项式遵循图2的设计规则,需引入Multiplier约束:
out ′ = RESET ⋅ freeIn + ( 1 − RESET ) ⋅ ( out ⋅ freeIn ) \text{out}' = \text{RESET} \cdot \text{freeIn} + (1 - \text{RESET}) \cdot (\text{out}\cdot \text{freeIn}) out′=RESET⋅freeIn+(1−RESET)⋅(out⋅freeIn)
在PIL中,多项式右上角的'表示该多项式下一行的值。
当该多项式基于某素数域 F \mathbb{F} F的某generator为 g g g的multiplicative subgroup G G G定义时,多项式右上角的'等价为 out ′ ( X ) : = out ( X g ) \text{out}'(X) := \text{out}(Xg) out′(X):=out(Xg)。
图2对应的PIL程序为:
 可见,RESET多项式定义中有constant关键字,表示其不会随着同一程序的多次执行而改变。
可见,RESET多项式定义中有constant关键字,表示其不会随着同一程序的多次执行而改变。
在不修改上述PIL程序的情况下,也可将图2的设计扩展为多个输入的乘积运算,即仅需将RESET多项式简单扩展为:

其中:
- i i i表示行号,起始值为0。
- n n n表示参与乘积运算的输入数量。
3. 编译
使用https://github.com/0xPolygonHermez/pilcom,可将PIL程序编译为JSON文件。该JSON文件表示了PIL程序以及一些额外的metadata。后续https://github.com/0xPolygonHermez/pil-stark将以该JSON文件为输入,生成一个STARK proof。
令 S S S为PIL程序中出现的 基于某域 F \mathbb{F} F的所有多项式 的集合。
多项式identity f = 0 f=0 f=0对应一个约束,其中:
- f ∈ F [ S , S ′ ] f\in\mathbb{F}[S,S'] f∈F[S,S′],其中 S ′ S' S′为 p ∈ S p\in S p∈S的所有shifted多项式 p ( g X ) p(gX) p(gX)的集合。
PIL中的限制为:
- f f f的degree必须小于等于2。
如图2对应PIL程序中的约束:
out ′ = RESET ⋅ freeIn + ( 1 − RESET ) ⋅ ( out ⋅ freeIn ) \text{out}' = \text{RESET} \cdot \text{freeIn} + (1 - \text{RESET}) \cdot (\text{out}\cdot \text{freeIn}) out′=RESET⋅freeIn+(1−RESET)⋅(out⋅freeIn)
可将其看成是多项式identity f = 0 f=0 f=0,其中:
f = out ′ − RESET ⋅ freeIn − ( 1 − RESET ) ⋅ ( out ⋅ freeIn ) f=\text{out}' - \text{RESET} \cdot \text{freeIn} - (1 - \text{RESET}) \cdot (\text{out}\cdot \text{freeIn}) f=out′−RESET⋅freeIn−(1−RESET)⋅(out⋅freeIn)
有 f ∈ F [ out , out ′ , RESET , freeIn ] f\in\mathbb{F}[\text{out},\text{out}',\text{RESET},\text{freeIn}] f∈F[out,out′,RESET,freeIn],但因 f f f中包含 RESET ⋅ out ⋅ freeIn \text{RESET} \cdot \text{out}\cdot \text{freeIn} RESET⋅out⋅freeIn 项, f f f的degree大于2,不满足PIL的限制。
为解决该限制,需在PIL程序中再引入一个新的名为carry的多项式,用于存储 out ⋅ freeIn \text{out}\cdot \text{freeIn} out⋅freeIn,即:
carry = out ⋅ freeIn \text{carry}=\text{out}\cdot \text{freeIn} carry=out⋅freeIn
类似carry这样的多项式称为intermediate多项式。
Prover无需提供intermediate多项式,因为Prover可直接根据committed多项式和constant多项式直接派生出intermediate多项式。Prover仅需要知道计算intermediate多项式的方法即可。
因此,引入carry intermediate多项式之后,PIL程序修改为:

此时,已知某有效PIL文件(后缀名为.pil),pilcom编译器将返回一个JSON文件,如:
pilcom$ node src/pil.js multiplier.pil -o multiplier.json
除输出JSON文件之外,pil编译器还会在控制台上打印如下debug信息:
Input Pol Commitments : 2
Q Pol Commitments : 1
Constant Pols : 1
Im Pols : 1
plookupIdentities : 0
permutationIdentities : 0
connectionIdentities : 0
polIdentities : 1
这些debug信息分别与PIL代码中的如下信息对应:
- Input Pol Commitments:对应committed多项式数量。
- Constant Pols:对应constant多项式数量。
- Im Pols:对应intermediate多项式数量。
- polIdentities:对应identity约束总数量。
- Q Pol Commitments:对应quotient多项式数量。【与intermediate多项式数量有关?对应有一个intermediate多项式计算规则:
pol carry = out * freeIn。】
PIL的关键特性之一是支持模块化,可在不同的.pil文件中以include进行依赖引用。
如在config.pil文件中定义多项式的degree bound等配置相关信息,在另一个multiplier.pil文件中可直接引用。
- 以constant关键字来定义常量值。为便于与其它多项式标识符区分,常量变量名以%标记。
4. Cyclic周期性约束
因execution trace具有有限长度 N N N,在设计PIL程序时具有内含复杂性:
- 对于 F ∗ \mathbb{F}^* F∗内size为 N N N的某subgroup G = < g > G=
即意味着,若某些约束不满足于每一行的变化,则以约束表示的该程序的描述是不正确的。原因在于,基于execution trace的列构建的多项式是基于 G G G插值而来的。
特别是,若约束中具有以 ′ ' ′标记的多项式,则意味着由最后一行到第一行的变化 也应满足相应的约束限制,原因就在于 g ⋅ g N = g ⋅ 1 = g g\cdot g^N=g\cdot 1=g g⋅gN=g⋅1=g,从而根据Lagrange定理有:
p ′ ( g N ) = p ( g ⋅ g N ) = p ( g ) p'(g^N)=p(g\cdot g^N)=p(g) p′(gN)=p(g⋅gN)=p(g)
对应为多项式该列的第一个值。
在设计PIL程序的约束集时,应注意上面的这个信息。若某约束在最后一个变化(有最后一行到第一行)不成立,则需再额外引入一个多项式来解决该问题。
如PIL代码为:

具有如下有效execution trace:
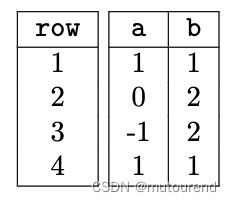
观察可发现,对于第一个约束( a +1) * a *( a -1) = 0,对所有行都成立。
对于第二个约束,b’ = b + a ,除最后一行外也都成立,原因在于:
![]()
其中 g g g为 size 为4的group G G G的generator。
解决该问题的思想为:增加一个常量列SEL,其在最后一行为0,而在其它行均为1,并将第二个约束调整为:

从而使得该约束对于 最后一行到第一行的变化 仍成立。
相应的有效PIL代码为:

5. Inclusion Argument
第2章中的Multiplier例子存在一个微妙之处在于:
- 其假设列中可包含field elements,这就意味着需限制列中值的size的位数为不超过特定数量。
为此,需开发一种策略,来同时控制underflow和overflow。
本章,将设计一个程序及其PIL,程序对应验证2个整数的加法,要求这2个整数的size正好为2字节。若整数不在 [ 0 , 65535 ] [0, 65535] [0,65535]范围内,则该输入无效。
有多种方式来对该程序进行算术化。但本章,将采用inclusion argument来实现。总体思想为将2-byte addition reduce为 1-byte addition。该程序包含2个input多项式a和b,每一行,引入求和项中的单个低有效字节(等价为,整数取值范围为 [ 0 , 255 ] [0,255] [0,255])。使得每两行,可检查一个new addition。
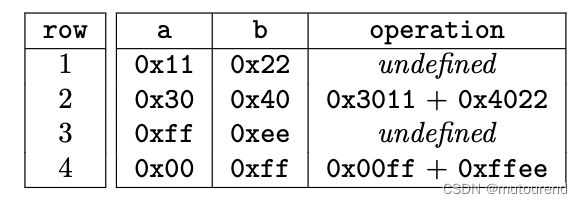
1-byte addition时需考虑overflow溢出问题,即将求和结果分为carry和add两列,每列也正好对应1个字节:
![]()
如下图,展示了该程序的一个valid execution trace示例。2-byte addition的结果为最后一个carry值和最后2个add值按降序排列组成。如0x3011+0x4022=0x007033(见下图的蓝色单元格),0x00ff+0xffee=0x0100ed(见下图的粉色单元格):
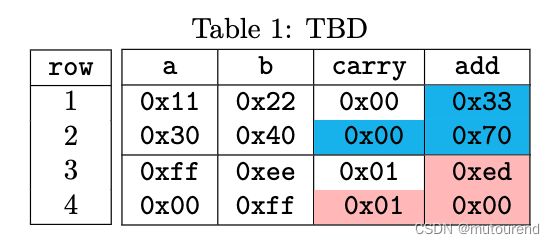
不过,对于上图一行,并不满足 a + b = c a r r y ⋅ 2 8 + a d d a+b=carry\cdot 2^8+add a+b=carry⋅28+add,因为第3行的carry值必须引入到第4行中,才能正确表示2-byte求和结果。不过,PIL语法中没有直接的方式来引入前一行的值,仅有'语法来引入下一行的值。为此,需要引入另一名为prevCarry的committed多项式,作为carry多项式的shifted版本,即有:

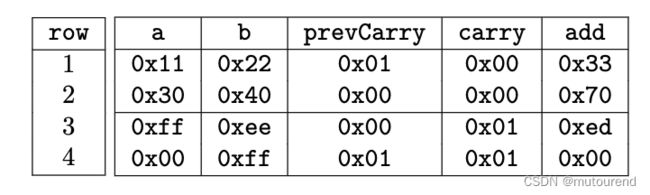
现在需要解决的问题就是,prevCarry值必须不影响每个约束中2个不同2-byte addition,即,不相关的运算不应通过prevCarry而关联。为此,需再引入名为RESET的constant多项式,打破现有的不同additions之间的关联。RESET为二进制值多项式,在每个2-byte addition的初始行,其取值为1,其它行为0:

根据该逻辑,最终的约束表示为:
![]()
相应的PIL程序为:

与第2张的Multiplier例子类似,在不修改PIL代码的情况下,仅调整RESET多项式,可将该程序扩展为verify generic n n n-bytes additions——此时RESET每隔 n n n行为1,其它所有行为0。
此时,可将约束(4)a + b + (1 − RESET) · prevCarry = carry · 2**8 + add 看成是该程序的sound representation。但是,当基于有限域 p p p时,该约束是不够的。如下图中,其execution trace可满足所有约束,是有效的,但这并不对应某有效计算:

此外,也没有任何机制来避免在任意列中引入更多的字节,即不满足具有固定byte size列的设计初衷。为此,有必要对所有committed多项式的evaluations值严格强化相关限制——可使用Inclusion argument。
在PIL上下文中,以in关键字来表示inclusion argument,其所实现的inclusion argument 为:
- [GW20] plookup: A simplified polynomial protocol for lookup tables论文中提出的inclusion argument,+,[PFM+22] PlonKuP:Reconciling PlonK with plookup论文中的“alternating method”。
如已知两列a、b,以 {a} in {b} 来表示inclusion argument,其中a、b可定义在不同的程序内,如:

以N=4为例,有效的execution trace示例为:

在PIL中,不仅可对单个列写inclusion argument,还可对多个列做inclusion argument。即,已知某程序的2个committed列subset a 1 , ⋯ , a m a_1,\cdots,a_m a1,⋯,am和 b 1 , ⋯ , b m b_1,\cdots,b_m b1,⋯,bm,以 { a 1 , ⋯ , a m } in { b 1 , ⋯ , b m } \{a_1,\cdots,a_m\} \text{ in } \{b_1,\cdots,b_m\} {a1,⋯,am} in {b1,⋯,bm} 表示列 { a 1 , ⋯ , a m } \{a_1,\cdots,a_m\} {a1,⋯,am}所有行的值 包含在 列 { b 1 , ⋯ , b m } \{b_1,\cdots,b_m\} {b1,⋯,bm}所有行的值 中。
这种跨多列的inclusion argument 对应 程序中某column集合的重复计算,这些计算可能具有相同的inputs/outputs pair,如跨不同程序的AND运算:

仍以之前的2-byte addition为例,为限制每个求和项固定为2个字节,需引入4个新的constant多项式BYTE_A、BYTE_B、BYTE_CARRY、BYTE_ADD,包含所有可能的byte additions,这些常量多项式的execution trace为:
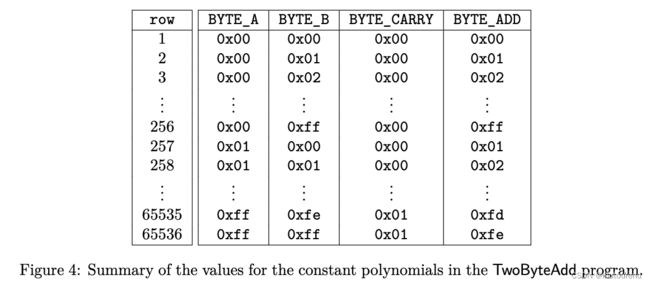
无需对BYTE_A、BYTE_B、BYTE_CARRY、BYTE_ADD多项式添加约束,因为这些多项式是常量的,对Prover/Verifier均为公开已知的。

通过inclusion argument,可确保(a, b, carry, add)被包含在上述constant多项式取值table中,从而可确保该程序的sound description。该inclusion argument:
- 不仅可确保所有的值为单个字节
- 还检查了addition的正确计算:当然这会给PIL程序引入某种冗余,即做了2次检查:
除在inclusion argument做了byte运算检查之外,在多项式约束a + b + (1 − RESET) · prevCarry = carry · 2**8 + add中还做了一次检查。
但是,我们不能简单地就去掉多项式约束,因有必要关联属于同一addition的rows。
借助inclusion argument,可发现Figure 3中没有任何一行包含在Figure 4的table内,因此可将Figure 3标记为无效。
完整的2-byte addition PIL程序为:

使用pilcom编译的debug信息有:

其中:
- plookupIdentities:对应PIL程序中的inclusion argument数量。如本例中数量为1。
5.1 避免冗余
可进一步修改来避免PIL中的冗余。需再引入另一constant多项式BYTE_PREVCARRY。由BYTE_A、BYTE_B、BYTE_PREVCARRY、BYTE_CARRY、BYTE_ADD组成的table 应遍历(BYTE_A, BYTE_B, BYTE_PREVCARRY)的所有可能组合,并为每种可能组合计算相应的BYTE_CARRY和BYTE_ADD。由于BYTE_PREVCARRY的取值为0或1两种可能,总的可能组合数为:2562562=131072,即新的table比之前的table大2倍。
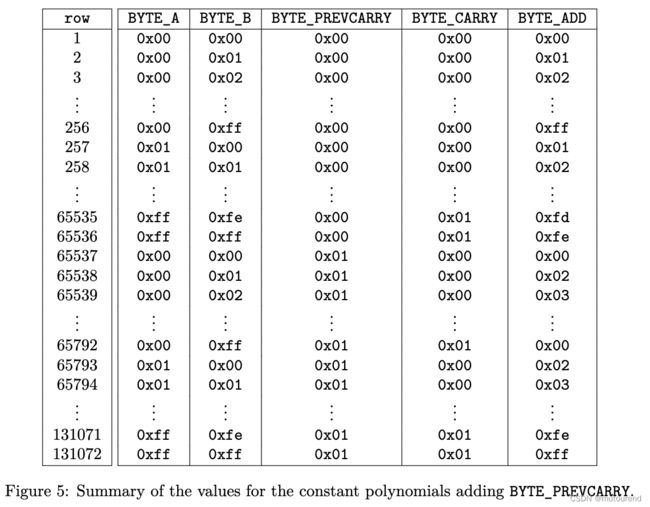
此外,仅当RESET为0时,才需要考虑prevCarry,因此在PIL中以Plookups来灵活解决该问题。相应的inclusion check变为:

对应的PIL程序为:

6. Connecting程序(多个程序连接引用)
PIL的核心特性之一是支持程序的模块化设计。借助模块化,可将某程序 M M M切分为多个小程序,对这些小程序的合理组合可构成 M M M。若没有模块化特性,需要在单个设计中组合多个片段逻辑,在设计中会引入大量的冗余多项式,且这种大设计难于验证和测试。
本章的例子为:设计一个程序来验证 a ⋅ a ˉ a\cdot \bar{a} a⋅aˉ运算(其中 ⋅ \cdot ⋅表示乘积运算),其中 a a a为4-bits整数, a ˉ \bar{a} aˉ为bitwise negation of a a a。难点在于,当直接处理4-bits chunks,很难描述bitwise operations。具体思想为,在另一程序中将其切分为bits,然后以trivial方式来检查该运算。
主程序中包含3列:a、neg_a(对应 a ˉ \bar{a} aˉ)、op(对应 a ⋅ a ˉ a\cdot \bar{a} a⋅aˉ)。该程序的有效execution trace示例为:
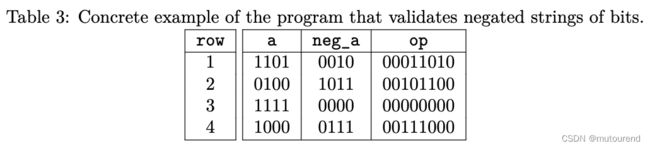
首先,需强化每个input是4-bit整数(即取值范围为 [ 0 , 15 ] [0,15] [0,15]),可借助inclusion argument来实现。此时,inclusion argument可强化一组值均在某特定(公开已知的)范围内。也因此,会将这类inclusion arguments称为range checks。对列a的range check PIL代码为:
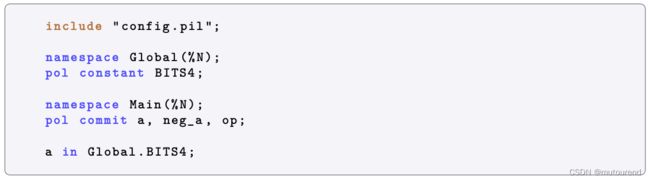
其中:
- BITS4:为包含所有4-bits整数可能取值的常量多项式。可以以任意顺序来构建,因为inclusion checks不关心顺序。
- BITS4定义在不同的namespace,引用另一namespace多项式的格式为:Namespace.polynomial。不过惯用方式是将不同的namespace放入不同点文件内,再使用include关键字来“connect”,如:

不过,直接处理4-bits是困难的。可设计另一个处理bitwise的程序,该程序包含了bits列,可存储单个bit,bits列的值按 a a a的little-endian bit排序(低位在前)逐行表示。nbits列对应为bits列的negation表示。同时,为将Main程序与Negation程序关联,需额外引入名为FACTOR的常量多项式,在Negation程序中证明其正确对应了 ( a , a ˉ ) (a,\bar{a}) (a,aˉ)。如:
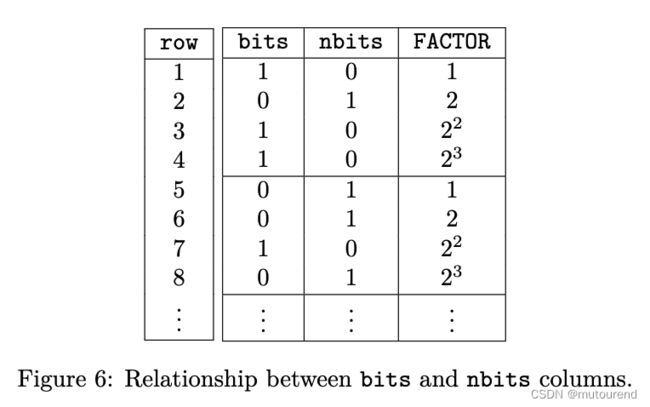
由于 b i t s ‾ = n b i t s \overline{bits}=nbits bits=nbits,且 b i t s , n b i t s ∈ { 0 , 1 } bits,nbits\in\{0,1\} bits,nbits∈{0,1},可将列bits与nbits的关系表示为:
b i t s + n b i t s = 1 bits+nbits=1 bits+nbits=1
与此同时,需引入常量多项式RESET,以便每4行重置分别根据bits和nbits对列a、neg_a的生成。由于 N = 2 10 N=2^{10} N=210可整除4,且为power of 2,该周期行为可满足。
对应PIL内的约束有:

Negation程序的完整execution trace示例为:【由于引入了RESET常量列,使得以上约束在每一行均满足。】
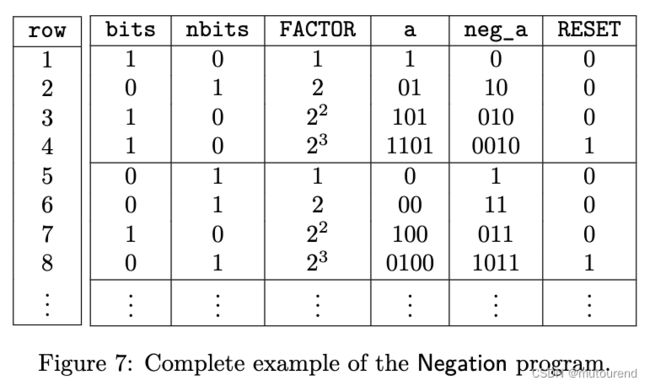
相应的negation.pil程序为:

注意,其中添加了对列bits和nbits的binary check,原因在于需确保二者为二进制位。
然后就可通过inclusion check来将Main程序与Negation程序关联了,如在Main pil的namespace中添加:

不过,PIL支持用户在inclusion checks中增加selectors,该特性具有极大的可塑性,支持用户在更小的execution trace row subsets间做inclusion check。如本例中,inclusion check中引入Negation.RESET selector,可针对更小的集合做inclusion check:

即强化为对 ( a , a ˉ ) (a,\bar{a}) (a,aˉ) 对 列a、neg_a的RESET为1的行所组成的更小集合 做inclusion check。
不过,由于程序自身设计,这将在PIL中引入冗余。令一面,也可在Main程序中增加sel selector:

对于某些inclusion仅在特定的row subsets下满足的特定场景,为PIL中的inclusion check引入selector至关重要,因为若无selector,相应的inclusion check在户部的rows subset中是无法满足的。此外,后续也将展示,引入selector,对于提升证明性能具有巨大重要性。原因在于,通过增加合适正确的selectors,可将rows之间的关系变为bijective,从而可将inclusion argument替换为permutation argument(详细见第8章),而permutation argument的效率要高很多。
也可在inclusion check中引入selector组合,如:

至此,Main程序引用了Negation程序,以验证特定列a的negation构建正确。但是,还需验证列a和neg_a的乘积,可简单在Main pil程序中引入约束:
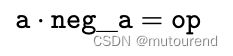
不过,由于我们本章在于展示多个程序间的连接引用,可直接用之前的Multiplier程序,在Main.pil中添加如下行即可:

总体的PIL程序代码为:
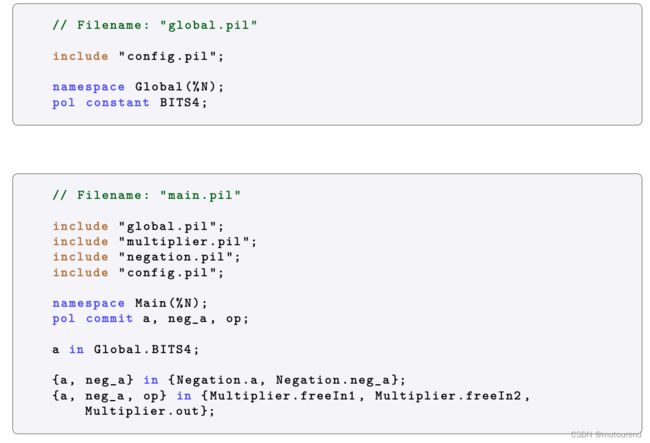

用pilcom编译main.pil的debug信息有:
![]()
7. Public Values
所谓Public Values,是指在算术化过程中,committed多项式中对Prover和Verifier双方均已知的值。如,若Prover声称其知道某特定计算的输出output值,则在算术化过程中,会在表示该计算的某些多项式内包含该public value(即output值)。本章,将使用public values来对某Fibonacci序列的算术化构建一个PIL程序。
Modular Fibonacci Sequence:
假设某人想证明其知道某初始2项为 F 1 , F 2 F_1,F_2 F1,F2的Fibonacci序列 ( F n ) n ∈ N (F_n)_{n\in \mathbb{N}} (Fn)n∈N的第1024项值为:
F 1024 = 180312667050811804 F_{1024}=180312667050811804 F1024=180312667050811804
每项值均会对 p = 2 64 − 2 32 + 1 p=2^{64}-2^{32}+1 p=264−232+1求模。
Prover秘密知道的witness input为 F 1 = 2 , F 2 = 1 F_1=2,F_2=1 F1=2,F2=1。
接下来以3列来对Modular Fibonacci Sequence进行算术化:
- 1)2个committed多项式a和b,已用于跟踪sequence elements。a和b间的约束有:
a ′ = b a'=b a′=b
b ′ = a + b b'=a+b b′=a+b - 2)常量多项式ISLAST用于确保即使在最后一行,1)中的约束也仍有效,即ISLAST的最后一行值为1,其它行值均为0。而最后一行(即第1024行)可确保生成的第1024项的值是否正确。从而将1)中的约束变为:
( 1 − I S L A S T ) ⋅ ( a ′ − b ) = 0 (1-ISLAST)\cdot (a'-b)=0 (1−ISLAST)⋅(a′−b)=0
( 1 − I S L A S T ) ⋅ ( b ′ − a − b ) = 0 (1-ISLAST)\cdot (b'-a-b)=0 (1−ISLAST)⋅(b′−a−b)=0
对应该Fibonacci Sequence的PIL程序为:

注意在该PIL程序中,将第1024个Fibonacci项固定写死为了 180312667050811804 180312667050811804 180312667050811804。如果想将该PIL程序用于其他witness F 1 , F 2 F_1,F_2 F1,F2,或者用于其他Fibonacci项,则需修改PIL程序中的该参数值。为避免这种情况,特引入public values。借助public values,Prover可在不修改PIL程序的情况下,调整witness F 1 , F 2 F_1,F_2 F1,F2或Fibonacci output值。
在PIL中采用如下语法来将a的最后一项当作是public value,其中括号内的整数对应为该项所在的行号:
public result = a(%N - 1);
编译器通过:冒号来区分public value标识符和其它标识符,如引用result public value值写成:result,据此更新的PIL文件如下:

8. Permutation Arguments
本章将介绍PIL中引入的一种新的约束类型:
- permutation argument
permutation argument定义为:

不同于inclusion argument,permutation argument中的2个向量必须具有相同的长度。在PIL上下文中,列a和b的Plookup permutation argument采用is关键字来表示,具体语法为:{a} is {b},其中a和b可定义在同一程序内,也可定义在不同程序内,如:

令 N = 4 N=4 N=4,相应的execution trace示例为:
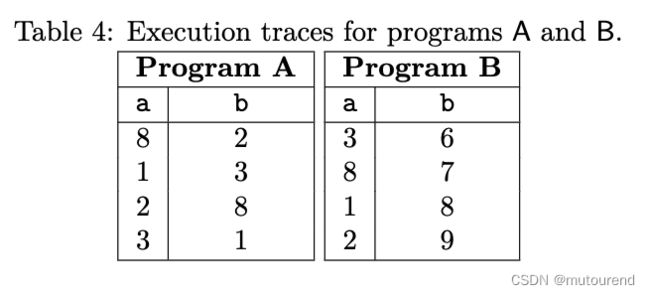
在PIL中,permutation argument不只可跨单列,也可跨多列。即,已知某程序的2个committed列subset a 1 , ⋯ , a m a_1,\cdots,a_m a1,⋯,am和 b 1 , ⋯ , b m b_1,\cdots,b_m b1,⋯,bm,可以 { a 1 , ⋯ , a m } \{a_1,\cdots,a_m\} {a1,⋯,am} is { b 1 , ⋯ , b m } \{b_1,\cdots,b_m\} {b1,⋯,bm}来表示列 b 1 , ⋯ , b m b_1,\cdots,b_m b1,⋯,bm中的各行值,为列 a , ⋯ , a m a_,\cdots,a_m a,⋯,am各行值的permutation。如:

不过,若整个列 set不满足permutation argument,而某个subset满足,可引入selector来表达,如:
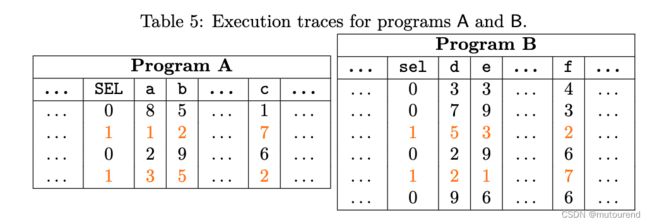
如上图所示,程序A的列{a,b,c} 仅在该trace的某subset内,为程序B的列{e,d,f}的permutation argument。为此,引入了committed列sel,将相应的行设为1以强化该permutation argument。当且仅当如下条件成立时,该permutation argument成立:
- 1)sel计算正确
- 2)2个程序A和B中由sel选中的行具有permutation关系。
相应的PIL程序可写为:

最后需注意,2个程序的sel列选中的行数应相同。否则,对于不同长度的向量,不存在permutation关系。这也意味着,借助selectors,即使2个程序的execution trace不具有相同的行数,也可使用permutation argument。
9. Connection Arguments(又名copy constraints)
本章将介绍PIL中引入的一种新的约束类型:
- Connection argument
已知某向量 a = ( a 1 , ⋯ , a n ) a=(a_1,\cdots,a_n) a=(a1,⋯,an)和对 [ n ] [n] [n]的partition S S S。Connection argument定义为:

令 § = { { 2 } , { 1 , 3 , 5 } , { 4 , 6 } } \S=\{\{2\},\{1,3,5\},\{4,6\}\} §={{2},{1,3,5},{4,6}}为 [ 6 ] [6] [6]的特定partition。对应有:
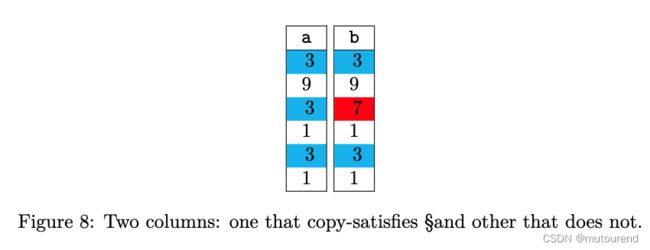
如上图所示,向量a copy-satisfy § \S §,原因在于 a 1 = a 3 = a 5 = 3 a_1=a_3=a_5=3 a1=a3=a5=3以及 a 4 = a 6 = 1 a_4=a_6=1 a4=a6=1。而 2 2 2为 § \S §中的单一项, a 2 a_2 a2不与向量a中的任何其它元素关联。但是,向量b不copy-satisfy § \S §,因为 b 1 = b 5 = 3 ≠ 7 = b 3 b_1=b_5=3\neq7=b_3 b1=b5=3=7=b3。
如[GWC19] PLONK论文中所示,通过引入关联了所选partition的某列,可很容易在PIL程序中编写connection argument。注意,column values为某多项式在 G = < g > G=
- 首先,需构建permutation σ : [ n ] → [ n ] \sigma:[n]\rightarrow [n] σ:[n]→[n],使得对于每个set S i ∈ § S_i\in\S Si∈§, σ ( § ) \sigma(\S) σ(§)中包含了a cycle going over all elements of S i S_i Si。如上例中,可设置 σ = ( 5 , 2 , 4 , 1 , 6 , 3 , 4 ) \sigma=(5,2,4,1,6,3,4) σ=(5,2,4,1,6,3,4)。
- 构建某多项式 S a S_a Sa,来encode σ \sigma σ in the exponent of g g g,即对于 i ∈ [ n ] i\in[n] i∈[n],有:
S a ( g i ) = g σ ( i ) S_a(g^i)=g^{\sigma(i)} Sa(gi)=gσ(i) - 在PIL上下文中,列a 和 编码了 S a S_a Sa值的列SA 之间的connection argument,可使用
connect关键字来声明,语法为{a} connect {SA}。

- Remark 1:SA列不要求必须声明为constant多项式,若声明SA为committed多项式,connection argument仍将成立。
- 有效的execution trace示例将Figure 8中的向量a。
connection argument可扩展至多列,其中每列编码了permutation的a “part”。这样,该permutation现在就可横跨所包含多项式中的每个值,在permutation内形成的cycles必须包含相同的值。
多列connection argument定义为:

如下图所示,有 § = { { 1 } , { 2 , 3 , 4 , 9 } , { 5 } , { 6 } , { 7 , 10 } , { 8 , 11 } , { 12 } } \S=\{\{1\},\{2,3,4,9\},\{5\},\{6\},\{7,10\},\{8,11\},\{12\}\} §={{1},{2,3,4,9},{5},{6},{7,10},{8,11},{12}},图中展示了copy-satisfy § \S § 的3个列a、b、c的execution trace:
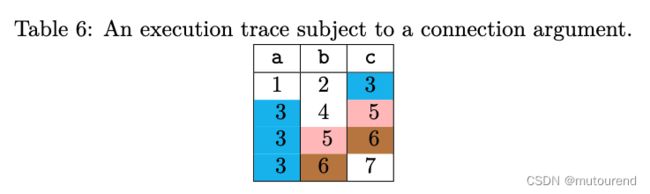
可将列a、b、c 拼接为一列,并将permutation σ \sigma σ用于该拼接后的单一列。相应的permutation σ = ( 1 , 9 , 2 , 3 , 5 , 6 , 10 , 11 , 4 , 7 , 8 , 12 ) \sigma=(1,9,2,3,5,6,10,11,4,7,8,12) σ=(1,9,2,3,5,6,10,11,4,7,8,12),此时构建的多项式 S a , S b , S c S_a,S_b,S_c Sa,Sb,Sc满足:
S a ( g i ) = g σ ( i ) , S b ( g i ) = k 1 ⋅ g σ ( n + i ) , S c ( g i ) = k 2 ⋅ g σ ( 2 n + i ) S_a(g^i)=g^{\sigma(i)}, S_b(g^i)=k_1\cdot g^{\sigma(n+i)}, S_c(g^i)=k_2\cdot g^{\sigma(2n+i)} Sa(gi)=gσ(i),Sb(gi)=k1⋅gσ(n+i),Sc(gi)=k2⋅gσ(2n+i)
其中引入 k 1 , k 2 ∈ F k_1,k_2\in\mathbb{F} k1,k2∈F 以 在size为 n n n的group G G G内获取更多的元素,从而可编码 [ 3 n ] → [ 3 n ] [3n]\rightarrow [3n] [3n]→[3n] permutation σ \sigma σ。详细的编码细节可参看[GWC19] PlonK论文。
上例SA、SB、SC多项式的计算规则为:
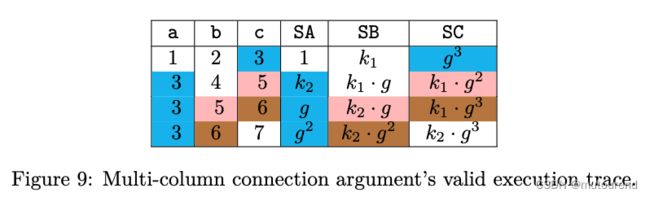
对应的PIL代码为:

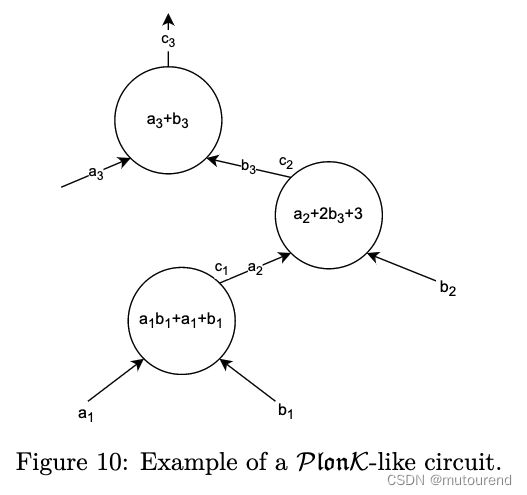
9.1 connection argument应用案例示意——PIL中的PlonK
作为应用案例示意,可使用connection argument来实现PlonK verification。假设有某PlonK-like电路C。在电路C中定义了一组预处理多项式QL、QR、QM、QO、QC来描述所有PlonK gates(即按gate被选中顺序对PlonK selectors进行插值),同时有3个connection多项式SA、SB、SC来指定所需满足的copy-constraints。SA、SB、SC connection多项式的构建方式与Figure 9中的方式一致。【standard PLONK约束 ( q L ) i a i + ( q R ) i b i + ( q O ) i c i + ( q M ) i a i b i + ( q C ) i = 0 (q_L)_ia_i+(q_R)_ib_i+(q_O)_ic_i+(q_M)_ia_ib_i+(q_C)_i=0 (qL)iai+(qR)ibi+(qO)ici+(qM)iaibi+(qC)i=0】
接下来将展示如何将上图PlonK电路转换为execution trace:
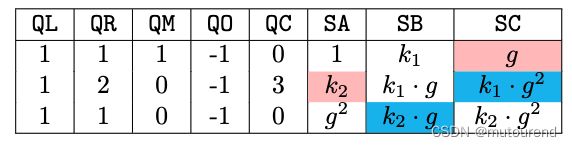
上图execution trace内的所有值均取决于电路形状本身,若电路不变,则相应的多项式也不需要重新计算。其中构建的SA、SB、SC多项式可验证电路中的 c 2 = b 3 c_2=b_3 c2=b3以及 c 1 = a 2 c_1=a_2 c1=a2 copy-constraints。注意其中带颜色的相等的单元格内的值做了交互,在之前构建connection S S S多项式时已解释过原因。
10. Filling Polynomials
至此,已介绍了PIL内某特定程序的多个多项式需如何满足特定类型的约束以确保程序执行正确。所有这些约束 + 计算本身所固有的常量多项式,可指定程序定义之下的transition function。换句话说,修改任意约束,或者修改常量多项式的描述,都可改变所处理的程序本身。
在本章,将使用Javascript和pilcom来为某PIL声称特定的execution trace。如,为第6章的例子计算某有效的execution trace。同时,也提供了pil-stark库——提供了setup、生成proof、验证proof的框架,使用FGL类来模拟某有限域,并使用pilcom包中所提供的某些函数。
-
首先,在名为execute的异步函数内,通过pilcom的compile函数,将所提供的PIL(如本例中,为main.pil)解析为一个Javascript对象。具体代码为:

-
pilcom包中还提供了2个函数,使用pil对象来创建 构建execution trace所需的至关重要的对象:
- 常量多项式对象:使用newConstPolsArray函数
- committed多项式对象:使用newCommitPolsArray函数

这2个对象内包含了PIL自身的有用信息,如程序的长度 N N N、常量多项式的总个数、committed多项式的总个数等。不过,访问这些对象可填充该PIL的整个execution trace。如访问execution trace的某特定位置 i i i的语法为:
pols.Namespace.Polynomial[i]其中:
- pols:为之前介绍的constPols和cmPols对象。
- Namespace:为PIL文件内定义的某特定namespace。
- Polynomial:为Namespace中定义的某特定多项式。
- i:取值范围为[0, N-1],表示取当前多项式的指定行。
这样就可以开始填充多项式了。
-
以第6章的例子为例,其execution trace的inputs,由Main.a多项式引入,由于限定为4 bits整数,其取值范围为0到15,此处假设其按为0到15循环取值。对constant多项式和committed多项式的填充示例代码如下:


-
此时有所有已填充的constant和committed多项式,可使用verifyPil函数来检查其确实满足定义在PIL文件内的约束。以下代码片段展示了构建多项式以及检查约束。如验证失败,则不应继续生成证明,因这将导致false proof。

11. 使用pil-stark来生成证明
一旦常量和committed多项式填充完毕,可进入proof generation环节。可使用pil-stark Javascript包 + pilcom来生成关于PIL statements的STARK proofs。
pil-stark中提供了如下3个函数:
-
starkSetup函数:用于设置STARK,与committed多项式的值无关。其中包含了constant多项式evaluation tree的计算。在执行setup时,必须有名为starkStruct的结构体,来指定多个FRI相关的参数——如trace domain size(必须与PIL中的 N N N一致)、extended domain size(与trace domain size一起,必须与之前的blowup factor参数一致)、需执行的query次数 以及 每个FRI step的reduction factors。如:

-
starkGen函数:用于生成STARK proof。在starkSetup函数返回的setup对象内包含starkInfo域内,除包含了所有starkStruct参数之外,还包含了许多关于PIL自身形状的有用信息。

-
starkVerify函数:STARK proof一旦生成,可调用starkVerify函数来验证。starkVerify函数需要的参数有starkSetup函数的输出 以及 starkGen函数的输出。若STARK proof有效,则starkVerify函数验证通过输出true。否则,Verifier应判定Prover所发送的proof是无效的。

参考资料
[1] Polynomial Identity Language (PIL): A Machine Description Language for Verifiable Computation
附录:Polygon Hermez 2.0 zkEVM系列博客
- ZK-Rollups工作原理
- Polygon zkEVM——Hermez 2.0简介
- Polygon zkEVM网络节点
- Polygon zkEVM 基本概念
- Polygon zkEVM Prover
- Polygon zkEVM工具——PIL和CIRCOM
- Polygon zkEVM节点代码解析
- Polygon zkEVM的pil-stark Fibonacci状态机初体验
- Polygon zkEVM的pil-stark Fibonacci状态机代码解析
- Polygon zkEVM PIL编译器——pilcom 代码解析
- Polygon zkEVM Arithmetic状态机
- Polygon zkEVM中的常量多项式
- Polygon zkEVM Binary状态机
- Polygon zkEVM Memory状态机
- Polygon zkEVM Memory Align状态机
- Polygon zkEVM zkASM编译器——zkasmcom
- Polygon zkEVM哈希状态机——Keccak-256和Poseidon
- Polygon zkEVM zkASM语法
- Polygon zkEVM可验证计算简单状态机示例
- Polygon zkEVM zkASM 与 以太坊虚拟机opcode 对应集合
- Polygon zkEVM zkROM代码解析(1)
- Polygon zkEVM zkASM中的函数集合
- Polygon zkEVM zkROM代码解析(2)
- Polygon zkEVM zkROM代码解析(3)
- Polygon zkEVM公式梳理
- Polygon zkEVM中的Merkle tree
- Polygon zkEVM中Goldilocks域元素circom约束
- Polygon zkEVM Merkle tree的circom约束
- Polygon zkEVM FFT和多项式evaluate计算的circom约束
- Polygon zkEVM R1CS与Plonk电路转换
- Polygon zkEVM中的子约束系统
- Polygon zkEVM交易解析
- Polygon zkEVM 审计及递归证明
- Polygon zkEVM发布公开测试网2.0
- Polygon zkEVM测试集——创建合约交易
- Polygon zkEVM中的Recursive STARKs
- Polygon zkEVM的gas定价
- Polygon zkEVM zkProver基本设计原则 以及 Storage状态机
- Polygon zkEVM bridge技术文档
- Polygon zkEVM Trustless L2 State Management 技术文档
- Polygon zkEVM中的自定义errors
- Polygon zkEVM RPC服务
- Polygon zkEVM Prover的 RPC功能