Reed-Solomon Codes及其与RISC Zero zkVM的关系

1. 引言

前序博客：

• Reed-Solomon Codes——RS纠错码

Reed-Solomon Codes当前广泛用于：

• QR codes二维码
• Cellular communication蜂窝通信
• STARKs

2. 简化的Reed-Solomon Encoding（RS编码）

所谓encoding（编码），是指：

• 将messages转换为codewords的系统。即：
  $Enc:\{messages\}\to \{codewords\}$

已知某encoding，code为所有可能codewords的集合。

所谓Reed-Solomon Encoding（RS编码），是指：

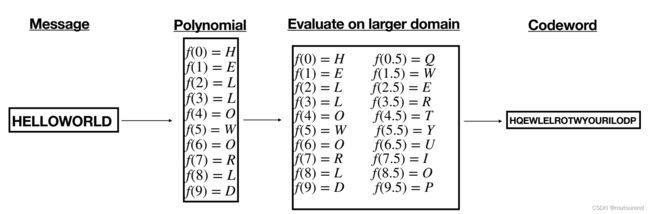
• 1）将a “message” 转换为 a polynomial
• 2）然后在 larger domain 对该多项式进行evaluate，以make a “codeword”
  
  那么问题来了：
• Reed-Solomon Encoding（RS编码）的好处是什么？
• Reed-Solomon Encoding（RS编码）与RISC Zero的关系？
• 具体的细节？
  • 如何构建$f$？
  • 如何选择“larger domain”？
  • 如何让其具备零知识属性？

2.1 RS Codes工作原理

以通讯为例，RS Codes可用于：【详情见Mary Wootters的代数编码理论第1讲notes】

• 探测错误（Error Detection）
• 纠正错误（Error Correction）

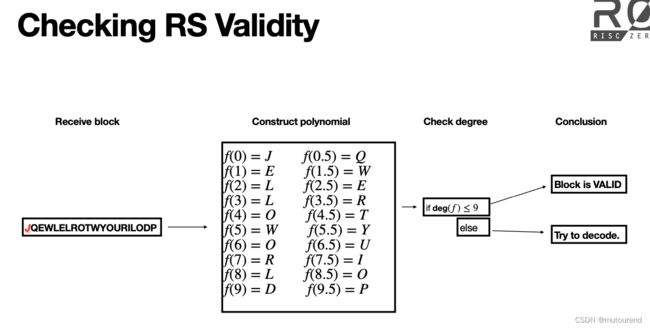
仍然以之前的“HELLOWORLD” message为例，因传输通道噪声，假设BOB收到的block为“JQEWLELROTWYOURILODP”而不是“HQEWLELROTWYOURILODP”。BOB可检查所收到的RS有效性：

• 1）基于所收到的block重构多项式$f$
• 2）检查该多项式$f$的degree：
  • 若$\mathrm{deg}(f)\le 9$，则说明所收到block是有效的；
  • 否则，该block无效，并试图对该无效block进行解码。
    

3. 对无效block解码

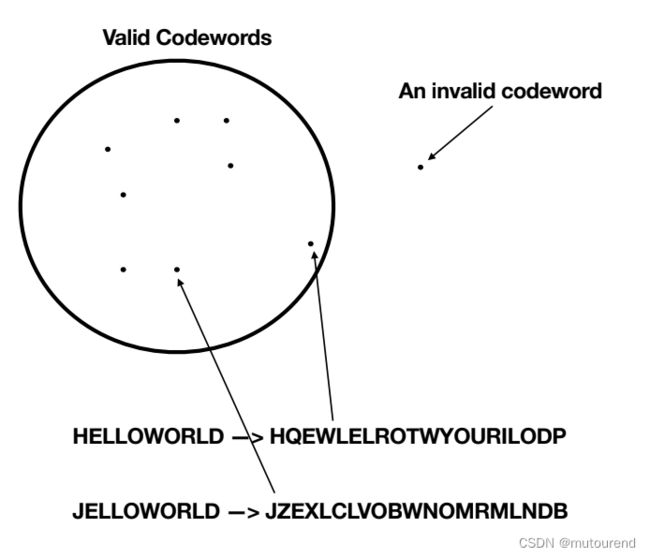
而BOB所接收到的无效block “JQEWLELROTWYOURILODP”对应的是invalid codeword：

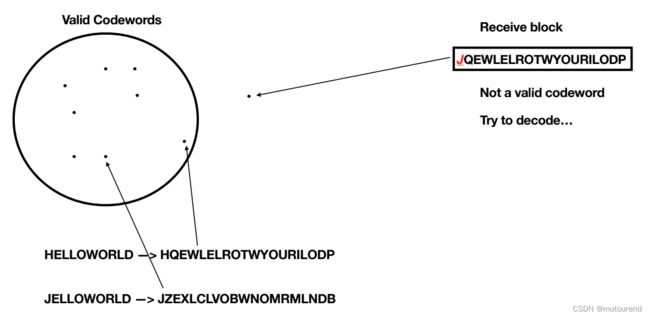
当试图对其解码时，需找到离其最近的valid codeword。判断2个codeword距离的标准为：

• $Distance(a,b)=$ 2个codeword之间不同的元素数量。即Hamming Distance。

为此有：

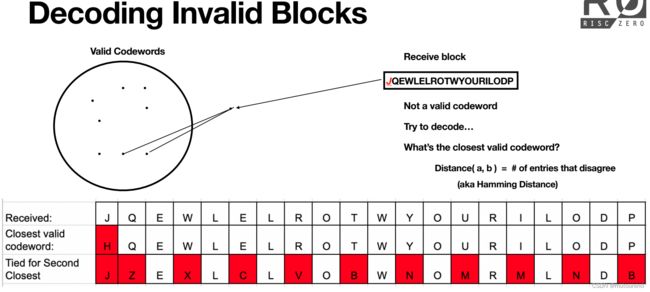
由此可知，离无效block “JQEWLELROTWYOURILODP”最近的codeword为“HQEWLELROTWYOURILODP”，据此BOB就可判断出ALICE试图发送的为"HELLOWORLD"，而不是"JELLOWORLD"。

Reed-Solomon encoding的一个关键特性是：

• 即使2个messages接近，但编码后的Reed-Solomon codewords相差很多。
• 如上图，消息"HELLOWORLD"和"JELLOWORLD"编码后的的codewords有多达11个不同之处。以上图为例，若2个有效的codewords有多达10个相同的元素，则这2个codewords是相同的，且对应的编码前消息也是相同的。
• 即Reed-Solomon encoding利用的是：2个low degree多项式无法具有很多重合点。从而可放大错误，使得可发现并纠正解码时的潜在错误。

4. RISC Zero中的Reed-Solomon Codes

RISC Zero中的Reed-Solomon Codes处理流程为：

• 1）Step 1 生成trace columns：在RISC Zero zkVM中执行某二进制文件，并记录其execution trace。
• 2）Step 2 将trace columns转换为trace blocks：采用Reed-Solomon Encoding对execution trace中的每列进行编码。
• 3）Step 3 对trace blocks之上的constraints进行evaluate，然后计算quotients：对trace blocks做STARK数学运算。
• 4）Step 4 应用FRI Protocol：让Verifier信服该结果是a valid Reed-Solomon codeword。

4.1 Step 1 生成trace columns

Step 1 生成trace columns：在RISC Zero zkVM中执行某二进制文件，并记录其execution trace：

• 任意代码在RISC Zero zkVM内执行时，其每个执行step都会记录在Execution Trace内。

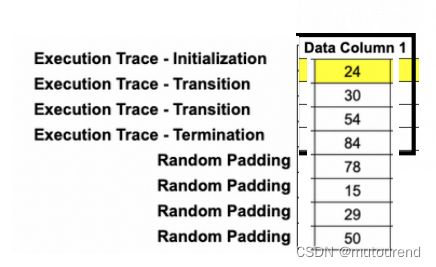
以具有2个用户指定输入，4个steps，并对97做模运算的Fibonacci序列为例，其execution trace为：

为引入零知识属性，需在各列引入随机padding，以Data Column 1为例，对其引入随机填充：【随机填充的行数，取决于FRI中query的次数。而不仅仅是最近的power of 2。每增加一行随机填充，会添加1个degree的freedom；每个FRI query，会偷掉1 degree的freedom。因此若想实现零知识属性，需至少添加 FRI query次数 行随机填充。同时，为支持能做(i)NTT，填充后的总行数，应为a power of 2。】

4.2 Step 2 将trace columns转换为trace blocks

Step 2 将trace columns转换为trace blocks：采用Reed-Solomon Encoding对execution trace中的每列进行编码。

仍然以Data Column 1为例，采用Reed-Solomon Encoding 对随机填充后的Data Column 1进行编码：

• 1）将a “message”转换为a polynomial：
  
• 2）然后在 larger domain 对该多项式进行evaluate，以make a “codeword”：【RISC Zero zkVM中，选择的larger domain为4倍大，即trace block为trace column size的4倍。】
  • 2.1）不过，不同于第2节中使用$1,2,3,\cdots$自然数序列来表达插值索引，为便于使用FFT提升效率，此处使用有限域内generator幂乘来表达插值索引：【以模97为例，取5为其generator】
    
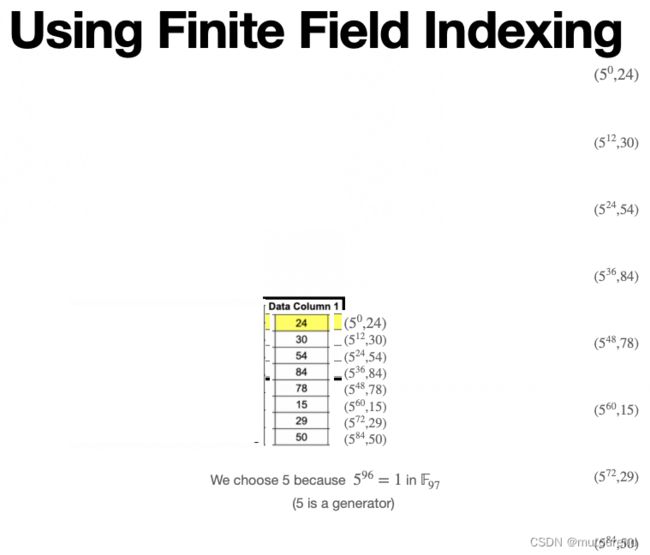
  • 2.2）然后在larger domain（此处为4倍）上对该以上以有限域插值索引的多项式进行evaluate，有：【同时为实现零知识属性，在large domain上的插值点是与原插值点$5^0,5^{12},\cdots$无交集的，即不再是$5^0,5^3,5^6,5^9,\cdots$，而是偏移的插值点$5^1,5^4,5^7,5^{10},\cdots$。】
    

4.3 Step 3 对trace blocks之上的constraints进行evaluate，然后计算quotients

Step 3 对trace blocks之上的constraints进行evaluate，然后计算quotients：对trace blocks做STARK数学运算。

对trace blocks做STARK数学运算：

• 基于约束规则，对Step 2输出的codewords做代数运算，即Step 3会生成类似的新的codewords。

不过，对codewords做代数运算，涉及如下实际问题：

• 1）2个valid codeword之和，是否为另一valid codeword？即：
  $a,b\in RS\stackrel{?}{}a+b\in RS$
• 2）多个valid codeword的线性组合，是否为另一valid codeword？即：
  $a_0,a_1,\cdots ,a_n\in RS\stackrel{?}{}{a}_0+{\alpha }^1{a}_1+\cdots +{\alpha }^n{a}_n\in RS$
• 3）若2个blocks为“close to valid”，则二者之和是否也为“close to valid”？即：
  $d(a,RS)<ϵ\&d(b,RS)<ϵ\stackrel{?}{}d(a+b,RS)<ϵ$
• 4）其它代数运算，如：
  • 4.1）若2个codeword之和为“close to valid”，那其中任一codeword是否为“close to valid”？即：
    $d(a+b,RS)<ϵ\stackrel{?}{}d(a,RS)<ϵ$
  • 4.2）若多个 codeword的线性组合为“close to valid”，那其中任一codeword是否为“close to valid”？即：
    $d(a_0+{\alpha }^1{a}_1+\cdots +{\alpha }^n{a}_n,RS)<ϵ\stackrel{?}{}d(a_i,RS)<ϵ$

4.4 Step 4 应用FRI Protocol

Step 4 应用FRI Protocol：让Verifier信服该结果是a valid Reed-Solomon codeword。

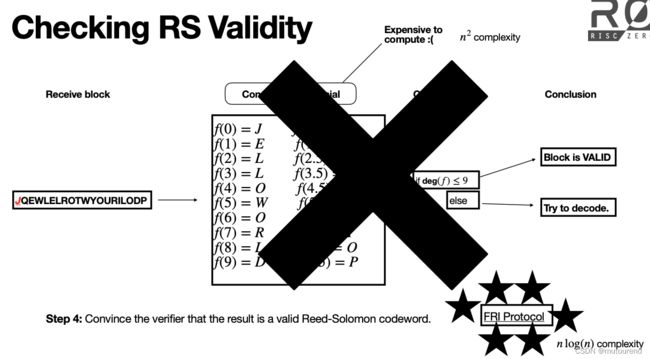
第2节中，Verifier为验证某Reed-Solomon codeword有效性，采用的方式为：

• 1）基于所收到的block重构多项式$f$：【重构多项式$f$计算太昂贵（复杂度为$O(n^2)$），对Verifier不实用】
• 2）检查该多项式$f$的degree：
  • 若$\mathrm{deg}(f)\le 9$，则说明所收到block是有效的；
  • 否则，该block无效，并试图对该无效block进行解码。

这种方式直观，但对Verifier来说，重构多项式$f$的计算太昂贵（复杂度为$O(n^2)$），为此，引入了FRI Protocol（复杂度为$O(n\log (n))$）：

对应的FRI协议示意为：

参考资料

[1] RISC Zero团队2022年11月视频 Reed Solomon Codes: RISC Zero Study Club【slide见An Introduction to Reed Solomon Codes】

RISC Zero系列博客

• RISC0：Towards a Unified Compilation Framework for Zero Knowledge
• Risc Zero ZKVM：zk-STARKs + RISC-V
• 2023年 ZK Hack以及ZK Summit 亮点记
• RISC Zero zkVM 白皮书
• Risc0：使用Continunations来证明任意EVM交易
• Zeth：首个Type 0 zkEVM
• RISC Zero项目简介
• RISC Zero zkVM性能指标
• Continuations：扩展RISC Zero zkVM支持（无限）大计算
• A summary on the FRI low degree test前2页导读