基于Nova/SuperNova的zkVM

1. 引言

本文为2023年3月13~4月7日 ZK Spring Residency in Vietnam上，由PSE团队、Orochi Network团队、0xPARC团队、Oskar（独立个人）以及Delv团队联合发布。

• Nova：借助Incremental Verifiable Computation（IVC）和 folding scheme，Nova可更高效地执行重复相同的代码块。
  Nova采用的安全假设为GLOG hardness以及RO（Random Oracle）。
• SuperNova：借助Non-uniform IVC（NIVC），SuperNova扩大的了Nova的应用范围，可执行不同的代码块。

Nova和SuperNova都可对计算中的关键部分进行并行化，且不需要FFT运算。从而可具有更快的proving time以及更少的memory usage。

将Intermediate Representation（IR）及其opcodes 映射为不同的IVC steps，从而可更高效地执行更小的重复代码块。这就利用了现有的编译器架构和hot-path优化。为此，提出了基于vector commitments来处理VM state updates的设计提案。每个computation step可折叠进某binary tree中，该binary tree可修正为可并行化的。final fold（最后一次折叠）可确保整个计算的完整性，并最终包裹进某SNARK中以实现succinctness。

本提案可用于证明ZK-WASAM执行以及ZK-LLVM执行，并以一个toy VM为例描述了具体的实现。

不同于EVM with gas对应的bounded computation execution，本提案重点关注unbounded computation execution，从而不像Halo2那样对roots of unity和memory consumption具有限制。

2. 背景资料

2.1 Incrementally Verifiable Computation (IVC)

Incrementally Verifiable Computation (IVC)是指，在每一步，基于某public state $z_i$和某extra witness input $W_i$，重复应用某step function $F$。
IVC中定义每一步的proof ${\pi }_i$用于证明：

• 前$i$步执行的正确性，即$F^i(z_0)=z_i$。

通常，使用SNARKs来递增构建${\pi }_i$。

2.2 Nova

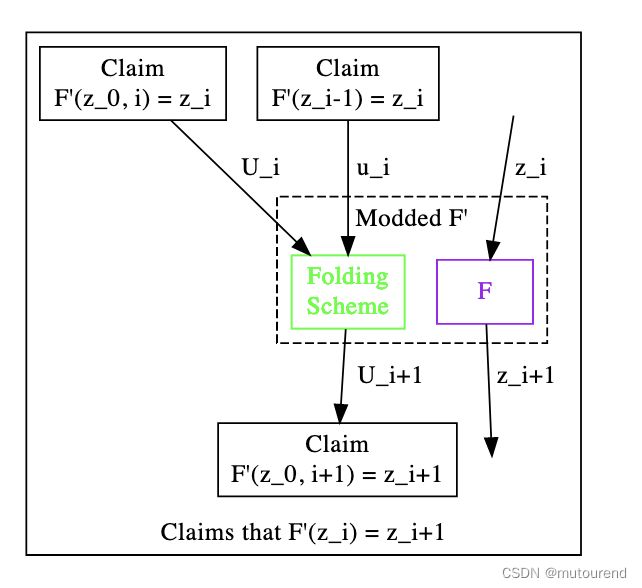
Nova使用IVC，但是，通过将SNARK Verifier 替换为 Folding Scheme，可有效降低recursion开销达一个数量级或更多。

借助Nova，在每一步，Prover仅需做$O(C)$次MSM（Multi Scalar Multiplications）运算。而若采用Halo，则每一步需要$O(C)$次FFT运算和$O(C)$次 EXP（在某密码group内的Exponentiations）运算。其中$C$为circuit size。

实际上，recursion开销对应约为1万个量级的约束。这意味着，对于具有更多约束的某指定function，折叠是有意义的。

2.3 SuperNova

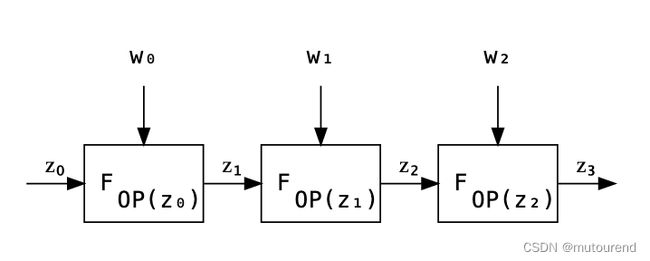
SuperNova将Nova扩展为支持Non-Uniform IVC（NIVC），这意味着可在每一步运行不同的函数。

借助Nova，将functions捆绑在一起并构建一个switch function，也可实现NIVC（Non-Uniform IVC）。但是，这样每一步的circuit size为$O(C\cdot L)$，其中$C$为对应该function的约束数，$L$为distinct functions数量。

而借助SuperNova，可并行维护$L$个running instances，每个对应一个function，并折叠当前step的proof到相关函数中。

3. SuperNova VM

VM由 顺序执行的指令集 + state（memory/stack） 组成。VM中的每个opcode对应IVC中的某step。可使用SuperNova来更高效地利用不同的opcodes，也可并行化证明每个step。将memory state变化 看做是每个step change对应的public input和output，并通过vector commitments（或者设计为其它）来实现。

借助SuperNova，在每一步可运行多个不同的函数，这样可友好地映射为VM中的opcodes。

在具有N条指令的模VM上下文中，Prover work由$O(N\cdot C\cdot L)$降低为$O(N\cdot (C+L))$，效果显著。对于$C>>L$的场景，意味着可无需过多关注opcodes的数量。

如EVM具有约100个量级的opcodes，WASM具有约400个量级的opcodes，可安全地假设$C>>L$，从而Prover time 变为$O(N\cdot C)$，其中$C$为每个opcode的平均约束数。

3.1 Nova并行化

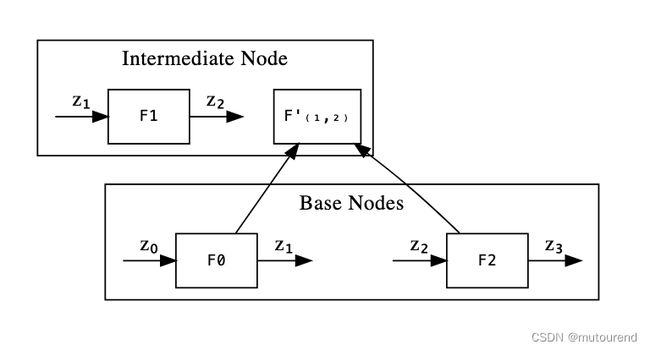
为并行化Nova，构建了a binary tree of computations，其中每个节点执行一个step。在该tree的root，可声称所有的计算以正确的顺序执行正确。

由于每个节点所需的计算可在不知道其它节点状态的情况下执行，因此可对其并行化。

如上所示意，可只计算是如何向上折叠的。更通用的情况为，$F^{\prime }(L,R)$对应为声称由step $L$到 step $R$执行正确，该声称为某承诺值。

而Nova论文中的基础场景为，$F(L,L)$，其中$F(Z_{L-1})=Z_L$，$Z_i$表示了public input和output。

可采用binary tree structure来对Nova 计算进行并行化。计算某single step的incremental proofs，然后fold “upwards”。即将step1-2 和 step3-4 转换为证明由 step[1-2] transition to step[3-4]。

在该binary tree的最顶端，可用于保证计算的完整性 以及 所有state transitions都是正确的。

当前：

• https://github.com/privacy-scaling-explorations/nova 中PSE团队做了parallel Nova的尝试。
• Distributed Nova Prover sketch 中讨论了尝试将Nova Prover以分布式方式运行，以实现并行化。

3.1.1 binary tree中的base node和internal node

在上述binary tree中，存在2类节点：

• base layer node：仅证明execution trace。每个base layer node证明依赖于应用$F$ instance所引起的state change。
• internal/intermediate node：也证明某correct step change。但此外，还证明the correct chaining of the previous output being equal to the actual input。同时，还会证明底层instance的折叠是正确的。

Nova中有2种不同的场景：

• base layer：要求提供witness的同时，表达整个execution trace（如上图的$F$ boxes）
• intermediate level：证明$F$的正确执行，并处理好折叠见public input/output的一致性，同时执行NIFS.Verify step。

3.1.2 Nova中所需的checks

为更详细的理解Nova中的折叠机制，先了解下所需的checks以及在每种场景下的工作原理。

由上图可知，base node和internal node之间的差异。绿色表示需执行的check，红色表示无需执行的check。为便于表达recursion，无论是否需执行该check，均图示包含表示。

3.1.2.1 base node所需的check

对于base node，仅需证明基于某input，运行$F$，可得到expected output。就证明给定某public inputs及，可获得某public outputs集，并forward给下一$F$ instance。

为此：

• 创建$F^{\prime }$ instance，来验证a dummy-initialized，并认同Prover与Verifier之间的folding instance，见NIFS.Verify step。【注意，此时事实上并不验证任何previous folds，仅将initial dummy fold与$F^{\prime }$ instance结合。】
• 需确保public input-output consistency。在base layer无需该step，且无 认可$F^{\prime }$ instance validation所需的initial inputs/outputs。

最终，简化为：

• 生成一组Relaxed R1CS constraints，并将其累加到新生成的instance matrix中（其中包含了error term computation 和 math-related folding ops）。这些约束用于证明实际的$F^{\prime }(z_L)=z_R$ relation成立。注意并不直接验证该relation成立，而是将其累加到最终的foldings中。
• 对previous folding verification做dummy checks。
• 对input/output consistency checks做dummy checks。

3.1.2.2 intermediate node所需的check

不同于base node，intermediate node具有$F$的输入，以及Relaxed R1CS instances pair的输入，可用于声称 previously folded $F^{\prime }$ instance pair为one computational step apart。

如上图所示，intermediate nodes的目的为：

• 强化Public Input/Output consistency的正确性，即检查F(left.out)=F(right.in)。
• 验证previous fold of $F^{\prime }$ nodes（NIFS）。

3.2 Curve Cycling

之前章节讨论了proof中$F^{\prime }$如何在每个new step验证某folding step。但是，缺少的关键细节为：

• 由于base filed 不等于 elliptic curve filed，约束若直接做field运算将非常昂贵。

为解决该问题，可一起运行two chains of folded proofs，把那个使用某elliptic curve cycle，使得某curve的椭圆曲线运算 可在另一曲线的base field上cheap验证。这将引入的recursive开销至少为$F^{\prime }$ circuit size，以及 sequential prover的每个step额外fold的proving time。

实际应用中，对于sequential场景，通过使用curve cycling来初始化2个relaxed R1CS instances，以及2个normal R1CS instances。proof中进行下一step的流程为：

• 1）在第二条曲线上折叠源自previous step的relaxed R1CS instance以及normal R1CS instance。

• 2）在第一条曲线上，为primary circuit构建新的$F^{\prime }$ R1CS instance，并将步骤1）中另一曲线的fold data作为$F^{\prime }$ folding verifier的输入。

• 3）在primary曲线上，将步骤2）中的new R1CS 与 input relaxed R1CS 折叠。

• 4）为步骤2）中的R1CS生成proof，并将步骤3）中的folding data作为$F^{\prime }$ verifier的输入。该R1CS instance声称：primary curve folding 以及 在第二曲线上$F$ circuit的正确性。

• 5）输出：

  • 步骤1）中的folding result
  • 步骤2）中的new claimed R1CS
  • 步骤3）的folding result
  • 步骤4）的new claimed R1CS

  作为每条曲线的Relaxed R1CS instance和normal R1CS instance 新pair。

最终，有另一曲线Nova sequence的folding validity Nova proof，每条曲线的circuit将触发$n$次。必须证明并验证每条曲线的Nova instance check了 另一条曲线的Nova instance。

下图证明了R1CS instances之间的关系。黑线表示folding关系，绿线表示验证关系，大写变量表示relaxed R1CS，小写变量表示normal R1CS。

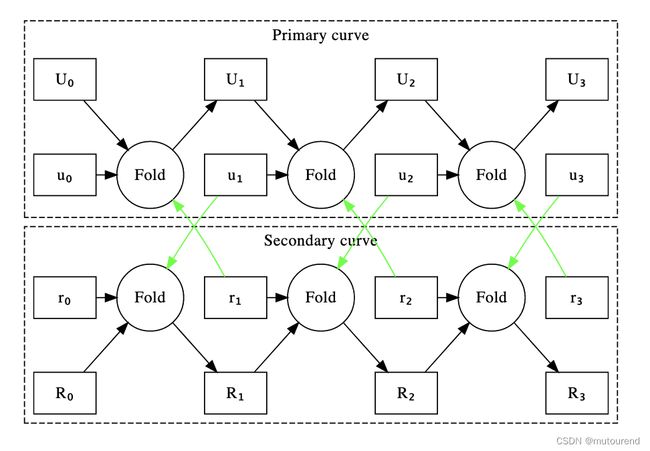
3.2.1 并行世界的Curve Cycling

直接将curve cycling用于之前的Nova并行实现将失败。因为$F^{\prime }$是针对sequential场景的，设计为仅能将1个relaxed R1CS 与 1个normal R1CS进行累计。在并行场景下，tree中每个节点同时具有：

• a relaxed R1CS instance：声称底层folding node proof的有效性。
• a new normal R1CS instance：声称下一次调用$F^{\prime }$。

为将这4个claims（声称）reduce为1个，需将2个relaxed R1CS instance和2个normal R1CS instance 折叠为1个relaxed instance，且$F^{\prime }$可验证该1/4折叠。

为尽可能复用微软的Nova代码，实际实现为3 foldings of 2 instances。当degree更高时，效率将很低。

为此，创建了新的 $u$，其为an R1CS claim：将tree中左边和有变动节点折叠为新的relaxed R1CS claim $N$。

3.3 SuperNova并行化

SuperNova的并行化要更复杂。
主要考量在于SuperNova设计为支持VM execution trace proving。即意味着对于每组opcodes，在每个fold中需支持每组opcode之一（并不清楚每个fold中有哪个opcode）。换句话说，并不清楚下一$F^{\prime }$ instance中所折叠的opcode。

现在，每次fold中包含尽可能多的opcodes和$F^{\prime }$ instances。

当前已知如何在Nova-style folds中支持多个opcodes，未知的是，如何在SuperNova中保证跨folds的内存、execution-order 以及 stack一致性，特别是在并行场景下。

为此，本文设计了一种在R1CS内具有可承受开销的SuperNova并行化方案。

3.3.1 使用vector commitments来更新state

其思想为：对$F^{\prime }$执行前后的memory state进行承诺，因此可open所希望的所有positions，并证明R1CS内部等于所运算的witness值。

VM的挑战之一在于确保内存的一致性。

借助vector commitments，可做如下操作：

• Open(Com, Idx) = Value
• Edit(Com, Idx, NewValue) = NewCommitment

vector commitments可对vector $a_0,\cdots ,a_{n-1}$进行commit，并证明某位置$i$的值为$a_i$。可用Kate承诺方案来实现：令$p(X)$为某多项式，对于所有的$i$，有$p(i)=a_i$。

注意：其足以匹配对所有内存位置进行承诺，且需要证明电路内部所提供的witness 满足 memory中特定位置的openings。

根据KZG polynomial commitments 可知，可通过Lagrange插值表示该多项式：
${\sum }_{n=0}^{n=i_{max}}Me{m}_i{\prod }_{n=0}^{n=i_{max}}\frac{X-j}{n-j}$

关于zkVM中的内存管理可参看：

• Proposal for Handling The Memory of zkVM

4. Nova bench

Nova benchmarks中指出，在https://github.com/privacy-scaling-explorations/nova-bench中，PSE团队对形如 $h(h(h(h(h(h(x))))))$ 的 recursively hashing of SHA256 $k$次的证明作了bench。

借助Nova+IVC，将其表示为：
$$h(h(h(x)))\text{(d times)}\to h(h(h(x)))\text{(d times)}\to \dots$$

不同证明系统性能对比为：

Framework	Arithmetization	Algorithm	Curve	Other
Circom (snarkjs)	R1CS	Groth16	Pasta
Nova (seq)	Relaxed R1CS	Nova	Pasta
Nova (par)	Relaxed R1CS	Nova	Pasta	parallel PoC
Halo2	Plonkish	KZG	BN254

在配置高的笔记本（Macbook Pro M1 Max (2021), 64GB memory）上，Prover time为：

k	Circom	Nova (total) d=1	Nova (step sum) d=1	Halo 2 (KZG)
1	0.3s	0.2s	0.1s	0.8s
10	7.3s	2.4s	1.2s	0.8s
100	62s	24s	12.5s	1.6s
1000	-	240s	125s	25s

在配置高的服务器（Server with 72 cores and ~350GB RAM）上，Prover time为：

k	Nova d=1	Nova d=10	Nova d=100	Nova d=100 par	Halo 2 (KZG)
100	19s	3.6s	-	-	2.5s
1000	190s	36s	26.5s	28.5s	41.6s
10000	1900s	360s	265s	226s	389.1s
100000	19000s				?

在配置高的服务器（Server with 72 cores and ~350GB RAM）上，不同证明系统的内存使用情况为：

k	Nova (seq) d=1	Halo 2 (KZG)	Nova (par PoC)
100	1.6GB	3.7GB	9GB
1000	1.6GB	32GB	244GB
10000	1.6GB	245GB	OOM
100000	1.6GB	?	?

不同证明系统的SRS size情况为：

• 对于Circom：当$k=100$ 约束数为300万时，需要23 powers of tau 或 structured reference string（SRS），$2^{23}$。对应为9GB文件，随着约束数增加线性增加，很快会变得不可用。
• 对于Halo2：为Plonkish。当$k=100$时，SRS size为$2^{18}$，$k=1000$时为$2^{22}$，$k=10000$时为$2^{25}$。由于计算更搞笑，Halo2所需的SRS要比Circom的短。
• 对于Nova：假设其原生运行，或，与Cirom C++ witness generator配合运行，都具有常量的内存开销。PSE库中采用Nova Scotia（将Circom电路编译给Nova prover的中间件）和Circom来编写带路，当$d=1$时，有约3万个约束，当$d=10$时，有30万个约束。以此类推。
• 对于并行化Nova：当前程序实现有bug，会引起内存线性增加。该bug由软件实现引起，并不是Nova内部机制导致的。

由此可知，Nova是内存高效的。

5. 应用

不同于zkEVM，zkWASM或通用VM中并无Gas的概念。

由于其底层的曲线具有有限的roots of unity，像Halo2或Groth16这样的证明系统具有hard time来表示VM execution traces。

递归可实现unbounded computation，但难点在于如何合理地切分execution trace。Plonkish类型的证明系统，由于其有大量的行或列，存在的缺陷是聚合较慢。

Toy VM中仅包含ADD和MUL指令，以及内存和program counter。详细见下面基于WASM的execution trace。

5.1 zkWASM

zkWASM的有趣点在于，WASM比EVM更通用，可打开隐私计算和验证计算的大门。如，用户想要证明在浏览器中访问某网址的WASM execution，或证明其sqlite db中包含某entry。

详细设计可参看：

• Extracting Execution Trace from WebAssembly Runtime

5.2 zkLLVM

与WASM类似，LLVM采用模块化架构，可添加新的backends并优化LLVM。该问题可转换为编译器优化问题。

5.3 zkRISC-V

RISC-V为基于现有R1CS原则的开源标准指令集架构。不同于ISA设计，RISC-V提供了开源license无需付费即可使用。

zkRISC-V为实现zkVM候选方式的优势在于：

• 支持目标机器的几乎所有编译器
• 开源标准且免费使用
• WASM opcodes可编译为RISC opcode
• 指令集标准化且不复杂

参考资料

[1] Towards a Nova-based ZK VM
[2] Nova-based ZKVM spec