zkVM设计性能分析
1. 引言
本文主要参考:
- 2023年9月ZKSummit10 Wei Dai @1k(x) & Terry Chung @1k(x)分享视频 ZK10: Analysis of zkVM Designs - Wei Dai & Terry Chung
当前有各种zkVM,其设计思想各有不同,且各有取舍,本文重点对现有各zkVM设计进行分析。
zkVMs寒武纪大爆发:
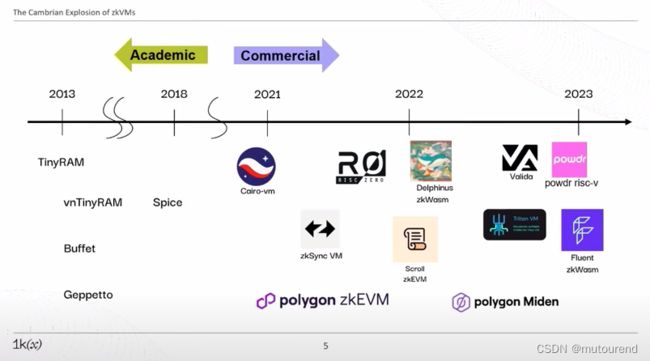
- 2020年之前的zkVM方案均是学术性的,不具备实用性,具体有:
- TinyRAM(2013年)
- vnTinyRAM
- Buffet
- Geppetto
- Spice等
- 2021年之后开始有商业化的zkVM方案,特别是近两年来各种zkVM方案开始大爆发,有:
- Cairo-VM
- Risc-Zero
- zkSyncVM
- polygon zkEVM
- Scroll zkEVM
- Delphinus zkWasm
- Valida
- Triton VM
- powdr risc-v
- Fluent zkWasm
- Jolt
- polygon Miden等
本文内容框架为:
- 何为zkVMs?为何需要zkVMs?
- zkVM设计性能分析:
- ISA性能分析
- Arithmetization性能分析
- Proof system性能分析
- 结论及开放性问题
2. 何为zkVMs?为何需要zkVMs?
2.1 为何需要zkVMs?
- 编程语言:zk Circuits通常采用Circom、HDL等面向领域编程语言编写;而zkVMs采用Rust、WASM、Risc-V、LLVM等高级通用语言编写。
- 易用性及生态:难于用zk Circuits来表达具有很多分支的复杂逻辑;而zkVMs的程序有大量现有可靠的软件。
- 性能:zk Circuits性能较高,因其对特定计算的约束进行了手动调优;而zkVMs性能要慢约10~100倍。本文重点关注的是如何提升zkVMs的性能。
2.2 何为VMs?
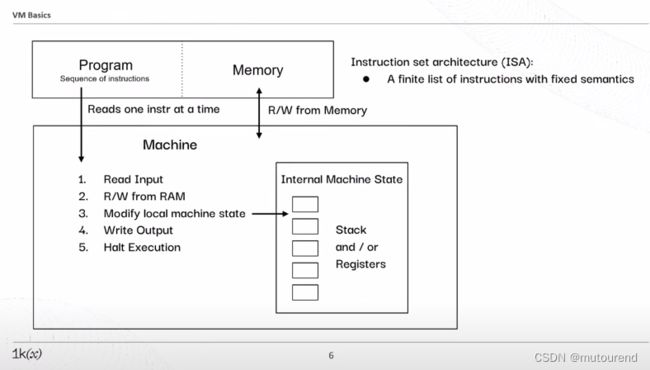
虚拟机采用指令集架构(Instruction set architecture,ISA),即:
- 具有固定语义的一组有限数量的指令集。
虚拟机(Virtual Machine,VM)的主要结构有:
- 程序:由指令序列组成。虚拟机每次仅读取程序中的一条指令。
- 内存
- 虚拟机:主要工作为:
- 1)读取输入
- 2)对内存(RAM)读写
- 3)修改本地机器状态:内部机器状态为:Stack和(或)Registers。
- 4)写输出
- 5)中止执行
现有的VM/zkVM架构,以及内部机器状态内存模型,选型情况为:

2.2.1 VM选择——Harvard架构 vs. Von Neumann架构
前序博客见:
- 哈佛架构 VS 冯·诺依曼架构
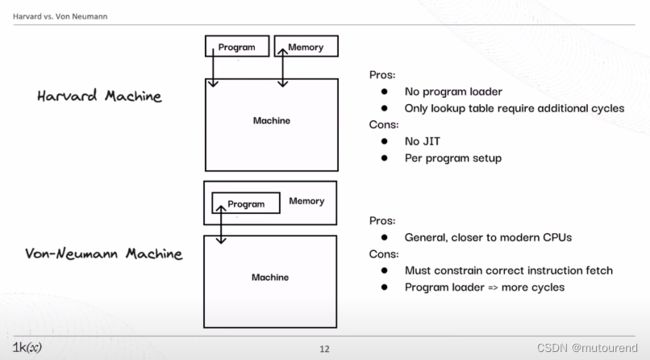
在做zkVM设计时,对应虚拟机(VM)架构通常需考虑在哈佛架构 和 冯·诺依曼架构 之间二选一:
- 哈佛架构:程序和内存分属不同区域。
- 优点为:
- 无program loader
- 仅lookup table需要额外的cycles。
- 缺点为:
- 无JIT
- per program setup(需对每个程序做setup)
- 优点为:
- 冯·诺依曼架构:程序在内存中。
- 优点为:
- 通用,更接近现代CPUs
- 缺点为:
- 必须约束所取指令的正确性
- 需要program loader(来将程序加载到内存中), 意味着需要更多cycles
- 优点为:
2.2.2 VM内部机器状态内存模型选择——Stack, Register, vs. Direct Memory
虚拟机内部机器状态内存模型,通常有3种选择:
- 1)Stack Machine:通过访问stack top来进行数据移动,指令更简单。如:
- EVM
- Miden-asm
- Wasm
- 2)Register Machine:指令比Stack Machine要短,但更复杂,不过数据移动操作要少的多。如:
- RISC-V
- 3)Direct Memory Machine:无需数据移动(zero data movement),但有更多的读写操作。如:
2.3 何为zkVMs?
zkVM的目的在于:
- 给定初始程序、初始程序输入、初始内部机器状态,证明以上VM的有效执行。
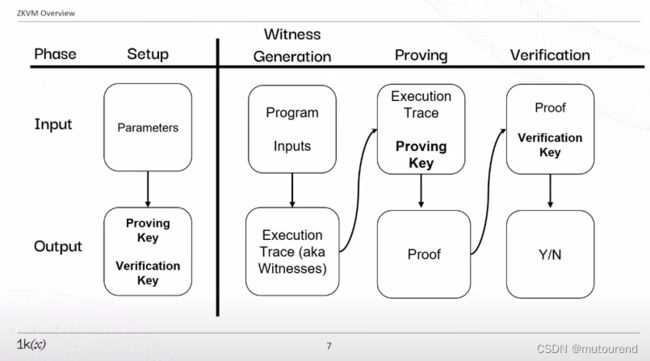
zkVMs主要分为四大阶段:
-
1)Setup阶段:根据参数(如最大trace行数、固定列数、哈希函数等),获得Proving key和Verification key。
-
2)生成Witness阶段:(Executor)根据程序和程序输入,生成execution trace(即witnesses)。该execution trace中包含了:
- 该程序的执行
- 以及,帮助约束该执行有效性的额外信息。
在生成Witness阶段,还包括将程序切分以供后续并行证明的工作。
-
3)Proving阶段:根据execution trace和Proving key,生成proof。
-
4)Verification阶段:根据proof和Verification key,生成验证是否通过的结果Y/N。
3. zkVM设计性能分析
传统虚拟机中,其效率分析的核心思想为:
- VM效率 约等于 (程序中的指令数 x 执行单条指令用时) ,即:
T ≈ P中指令数 × time instruction T\approx \text{P中指令数 }\times \frac{\text{time}}{\text{instruction}} T≈P中指令数 ×instructiontime
当使用zkVM证明某固定、抽象程序P时,借鉴相同的思想:
- zkVM效率 约等于 (程序中的指令数 x 单条指令的约束复杂度 x 单个约束证明用时) ,即:zkVM证明用时 T T T以如下公式来表示:
T ≈ P中指令数 × time instruction ≈ P中指令数 × "Constraint complexity" instruction × time "Constraint complexity" \begin{aligned}T &\approx \text{P中指令数 }\times \frac{\text{time}}{\text{instruction}} \\ &\approx\text{P中指令数 }\times \frac{\text{"Constraint complexity"}}{\text{instruction}} \times \frac{\text{time}}{\text{"Constraint complexity"}}\end{aligned} T≈P中指令数 ×instructiontime≈P中指令数 ×instruction"Constraint complexity"×"Constraint complexity"time
其中的“约束”为:
- 衡量某类proof system复杂度的单位。
取决于所采用的proof system类型,具体的“约束复杂度”是指,如:
- R1CS约束数
- 具有固定配置的Plonk电路中的cells数
- 具有固定depth的GKR电路中的wires数
为此,在对zkVM做性能分析时,将“(程序中的指令数 x 单条指令的约束复杂度 x 单个约束证明用时)”拆分成3个维度来分析,其中:
- 1)程序中的指令数:对应为ISA(Instruction set architecture)性能分析。
- 2)单条指令的约束复杂度:对应为Arithmetization性能分析。
- 3)单个约束证明用时:对应为Proof system性能分析。

3.1 ISA性能分析
ISA(Instruction set architecture)性能分析,主要关注的是程序中的指令数。
传统ISA和“ZK ISA”是针对不同的场景进行了优化:
-
传统ISA为:
- 内存局限性:处理器具有内存上限。
- 程序size(如压缩):无法有太多通用寄存器。
- 执行速度
-
"ZK ISA"为:
- 每个cycle,一条指令:具有指令上限。
- 指令大小的影响小:指令可包含更多信息,如引用更多寄存器或本地变量。
- 证明速度或性能。

以,在软件中实现SHA256 one-round压缩函数 所需的指令数,为例,不同虚拟机对比情况为:

其中:
- 前三种(EVM、Miden-asm、Wasm)为stack machine,具有相对更多的local data movement操作。
- RISC-V为register machine,具有少得多的local data movement操作。
- LLVM-IR为direct memory模式,具有虚拟寄存器,从而具有zero data movement。
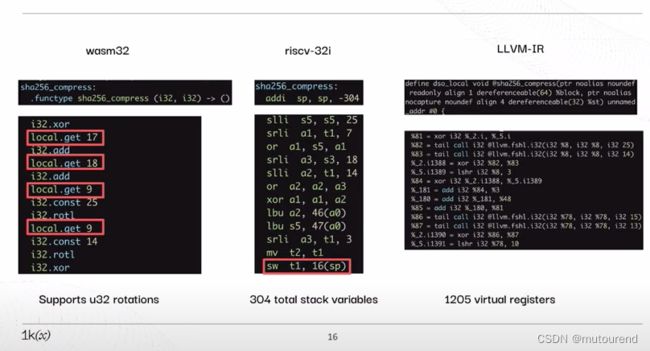

由此可知,实际的ISA性能,取决于所采用的机器内部状态内存模型:
- 1)Stack machines:具有大量stack操作(数据移动操作)(高达50%~60%)。
- 2)Register machines:
- 当寄存器压力低时,其性能好。
- 当寄存器压力高时(~30%),需要大量的数据移动。
- 3)Direct memory machines:
3.2 Arithmetization性能分析
Arithmetization性能分析,关注的是:
- 单条指令的约束复杂度。

实际在对Arithmetization性能分析时,主要分为2大块:
- Segment性能分析
- “Recursion复杂度”+“Continuation复杂度” 性能分析。
3.2.1 Segment性能分析
算术化是指将对程序执行segment的约束,转换为:
- Permutation check、
- Gate check、
- lookup、
- Copy check
等组合,然后进一步转换为2大类子约束表达:
- Zero check
- Product check
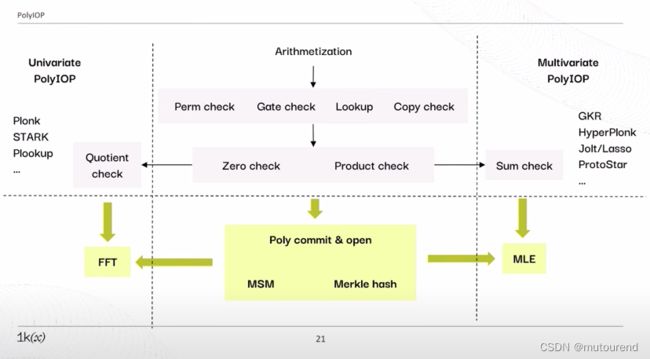
取决于具体所采用的PolyIOP方案,后续的方案以及影响性能的关键运算也有所不同:
- 单变量PolyIOP:相关方案有Plonk、STARK、Plookup等,对应为Quotient check,影响性能的关键运算为FFT。
- 多变量PolyIOP:相关方案有GKR、HyperPlonk、Jolt/Lasso、ProtoStar等,对应为Sum check,影响性能的关键运算为MLE。

以基于STARK的zkVM为例,将程序正确执行的execution trace切分为多个segment。其Prover的证明用时由:
- 派生多项式,以及对多项式进行承诺
所主导。根据RISC0、Triton、Plonky2所提供的数据:
- 经典的STARK Provers有60%~80%的证明时长用于派生和commit多项式。
3.2.1.1 STARK VMs vs. SNARK VMs
- Risc0
- Miden
- Cairo
- Valida
- Nock
- TritonVM
- zkSync VM
- Polygon zkEVM
这些STARK zkVMs的性能分析对比情况为:【关键数据见最后2列】

现有的基于SNARK方案的zkVMs,采用的都是基于Halo2的方案,具体有:
- zkWasm
- Powdr的Risc-v
- Scroll的zkEVM
3.2.2.2 segment性能提升措施
为提升Arithmetization segment性能,其目标应为:
- 尽可能使,单个指令的committed cells,数量最少。
具体措施有:
- 1)移除重复的cells。仅对每个指令的“state change”进行commit。
- 对“non-local” 数据/计算,采用permutation/lookups。
- powdr risc-v中的寄存器(编码在列中),占约50%的列。
- 2)采用表达性更好的IOP arguments:
- 3)具有“flexible area”的co-processors,有助于改进单个指令开销。
3.2.2“Recursion复杂度”和“Continuation复杂度” 性能分析

当将1个完整的execution trace切分为 t t t个segment时,总的复杂度为:
- 证明所有 t t t个(具有 n n n-step)segments复杂度
- 证明所有 t − 1 t-1 t−1个 recursive proofs的复杂度
相应的关键路径为:
- 1个segment proof
- log ( t ) \log(t) log(t)个recursive proofs
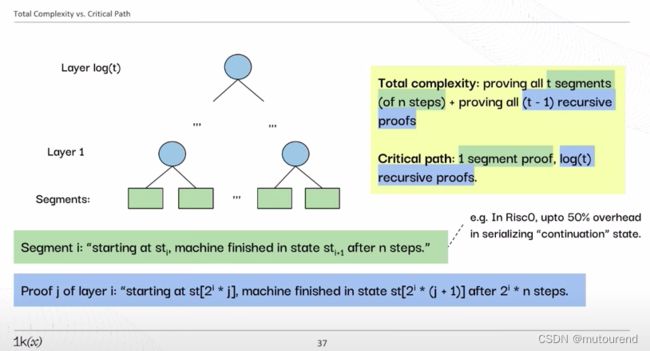
如Risc0中,有多达50%的开销用于对“continuation” state进行序列化。
对比SNARKs(Plonk)、Folding/Accumulation、STARKs等方案的recursion threshold开销为:


3.3 Proof system性能分析
Proof system性能分析,关注的是:
- 单个约束证明用时。
对于多项式承诺方案(PCS,Polynomial Commitment Scheme),基于FRI的PCS性能要由于基于MSM的多项式承诺方案性能:【其中y轴表示的是每秒承诺的域元素数】


4. 结论及开放性问题
关于ISA的开放性问题有:
- 如何将现有工具应用到zk-efficient ISA中?
- 可进一步消除data movement么?如对memcpy进行direct argument?
关于Arithmetization的开放性问题有:
- 降低单个指令的复杂度
- 降低递归(recursion)复杂度
- “doubly-fast”哈希函数(如Poseidon2、Tip5、XHash{8,12}、Monolith等)
- 降低"continuation"复杂度
关于proof system/PCS的开放性问题有:
- FFT、MLE、PCS应封装为库,项目方可受益于这些原语的更好实现。
- 更好的bench工具,来对比各个方案的性能。
参考资料
[1] 2023年9月ZKSummit10 Wei Dai @1k(x) & Terry Chung @1k(x)分享视频ZK10: Analysis of zkVM Designs - Wei Dai & Terry Chung【1k(x)为早期密码学投资基金】