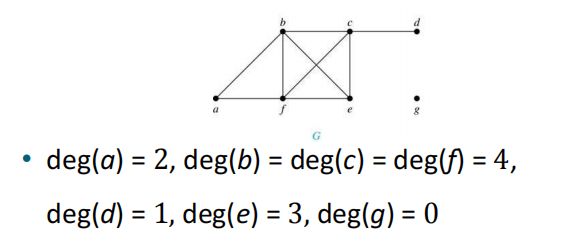离散数学期末复习(4):图论(Graphs)
目录
10.1 Graphs and Graph Models (图和图模型)
10.2 Graph Terminology and Special Types of Graphs (图的术语和几种特殊图)
1.基础概念
2. 度(degree)
(1)无向图中一个顶点v的度是这个点相关的边的数量,写作deg(v)
(2)握手定理
(3)出度和入度
3.图的分类
(1)圈图(Cycles)
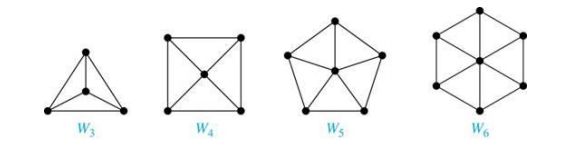
(2)轮图
(3)n维超立方体
(4)二部图(Bipartite Graphs)
4.子图
(1)概念
(2)导出子图
(3)删除边和添加边
(4)边收缩(edge contraction)
(5)图合并
10.3 Representing Graphs and Graph Isomorphism (图的表示和图的同构)
1.邻接
(1)邻接表
(2)邻接矩阵(adjacency matrix)
2.关联矩阵(Incidence Matrices)
3.同构(Isomorphism)
10.4 Connectivity (连通度)
1.路(path)
2.连通(connectedness)
(1)连通图
(2) 连通分支(connected components)
(3)强连通和弱连通
3. 割割割
(1)割点
(2)割边
(3)不可分割图
(4)点割集(vertex cut):割点组成的集合
(5)点连通度(Vertex Connectivity)
(6)边连通度 (Edge Connectivity)
4.计算顶点之间的路径数量
10.1 Graphs and Graph Models (图和图模型)
图的概念
图G = (V, E),V表示vertices(点),E表示edges(边),每一条边都有一到两个点连接着,这些点也被称为端点
点的数量有限的图被称为有限图,点数量无线被称为无限图
简单图:两点之间只有一条边连接的图
多重图(Multigraphs):每两个点之间有m(m>=2)条边相连,这里的m被称为重数
将顶点和自己连接的边被称为环
伪图(pseudograph):包含边和环的图
有向图(digraph):有箭头从始点指向终点的图
无向图:没箭头的图
10.2 Graph Terminology and Special Types of Graphs (图的术语和几种特殊图)
1.基础概念
如果两个点u和v之间由一条边e连接,这两个点被称为邻接点(adjacent),连接他们的边被称为关联(incident)。
G =(V,E)的一个顶点v的所有邻域的集合,用N (v)表示,称为v的邻域
2. 度(degree)
(1)无向图中一个顶点v的度是这个点相关的边的数量,写作deg(v)
一个环的度数为2
(2)握手定理
如果G =(V,E)是一个有m条边的无向图,则
(3)出度和入度
在有向图G中,(u,v)是一条边,这里的u是这条边的起点,v是这条边的终点。对于环来说,起点和终点是一样的。
入度:deg![]() (v),就是从外面射向点的边的数量
(v),就是从外面射向点的边的数量
出度:deg![]() (v),就是从点射向外面的边的数量
(v),就是从点射向外面的边的数量
边的总数量
3.图的分类
(1)圈图(Cycles)
(2)轮图
(3)n维超立方体
(4)二部图(Bipartite Graphs)
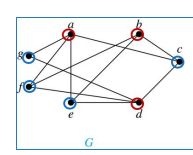
如果V可以被划分为两个不相交的子集V1和V2,这样每条边都连接着V1的一个顶点和V2的一个顶点,换句话说,在V1或V2中没有边连接来自同个点集的两个顶点
这里的G是一个二部图,所有顶点被划分成两个点集{a, b, d}和{g,f,e,c}
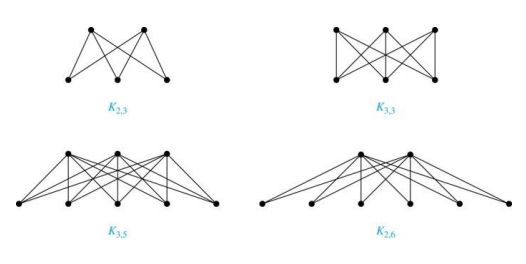
完全二部图
图Km,n,其顶点集划分为两个大小为m的子集v1和大小为n的v2的子集,这样从v1的每个顶点到v2的每个顶点都有一条边
匹配
点集里的一个点对应连接到不同点集的另一个点,就叫做匹配
最大匹配是这个点和另外一个点集里面的所有点能进行匹配的边的数量
完全匹配是点集v1里面的每个点和点集v2里面所有点都有最大匹配
4.子图
(1)概念
图G =(V,E)的一个子图(子图)是一个图(W,F),其中W⊂V和F⊂E
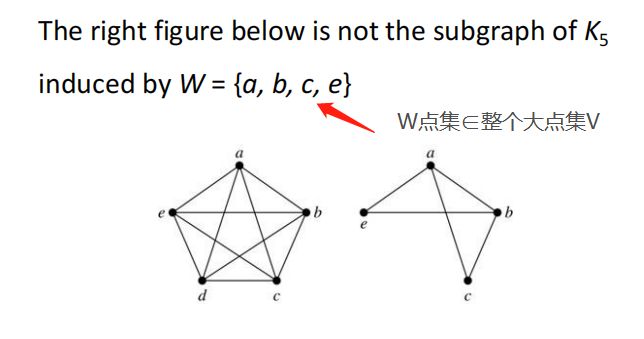
(2)导出子图
(3)删除边和添加边
(4)边收缩(edge contraction)
用一个顶点代替多个顶点,并把多条边浓缩成少量的边的过程
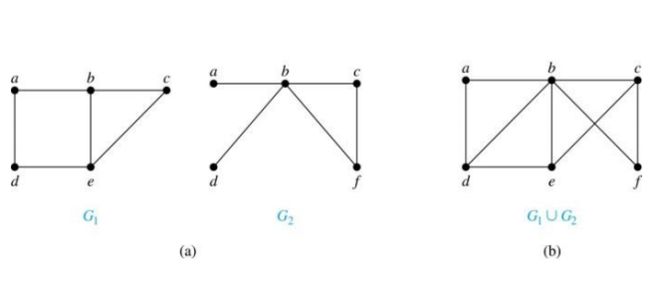
(5)图合并
10.3 Representing Graphs and Graph Isomorphism (图的表示和图的同构)
1.邻接
(1)邻接表
邻接表可以通过指定相邻于图的每个顶点的顶点来表示没有多个边的图
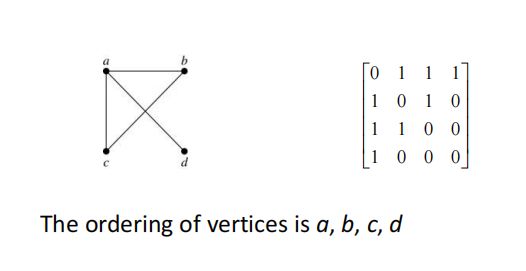
(2)邻接矩阵(adjacency matrix)
假设G是一个简单图,任意地将G的顶点列为v1,v2,……,vn
邻接矩阵A![]() 是一个n×n的零1矩阵,A
是一个n×n的零1矩阵,A![]() = [a
= [a![]() ]有下面的定义
]有下面的定义
伪图的邻接矩阵里面的项不一定都是0和1
有向图的邻接矩阵
2.关联矩阵(Incidence Matrices)
设G =(V,E)是一个无向图,其顶点为v1,v2...,vn,边为e1,e2...,em
关联矩阵M = [mij]是一个零1矩阵,而且有下面的定义
注意:邻接矩阵问的是点和点之间是否有边(简单图)和边的数量(伪图,多重图)
关联矩阵问的是点是否有在指定边上
3.同构(Isomorphism)
![]()
如何判断两个图是否同构
1.看点数目是否相同
2.看边数目是否相同
3.度数相同的点相邻点的度数是否相同
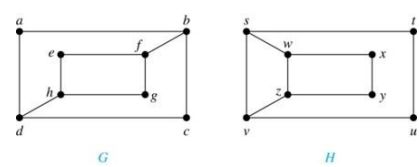
判断G和H是否同构
很显然G和H不同构,因为deg(a) = 2,说明G里面的a应该和H里面的t,u,x或者y相对应,但是t,u,x和y分别相邻的点的读书都是2,而a相邻的点(b和d)的度数为3, 所以这两个图不同狗
10.4 Connectivity (连通度)
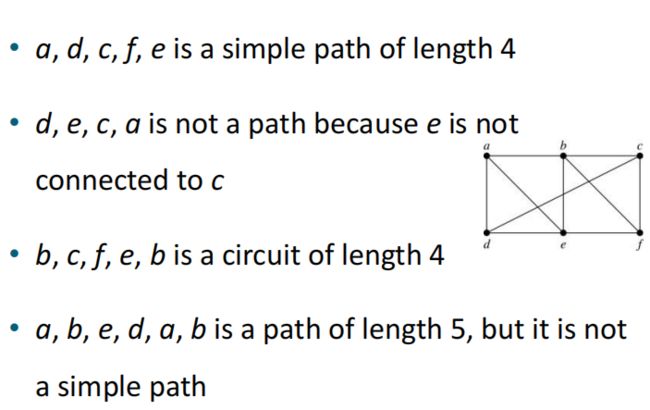
1.路(path)
路径(路)是一组边序列,它从图的顶点开始,沿着图的边从一个顶点移动到另一个顶点。当路径沿其边移动时,它会访问这条路径的端点。
路的长度指从a到b期间经过的边的数量(比如a和b之间有一个点c,a先到c再到b而且没有a到b的直达边,那就会有两条边,这时路的数量为2)
如果遇到环(或者走回头路了),走过相同的路就不再重复计算了
2.连通(connectedness)
(1)连通图
如果一个无向图没对顶点之间都有一天路径,这个无向图就被称为连通图。反之为不连通图。
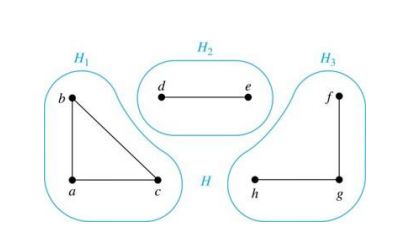
(2) 连通分支(connected components)
G的连通分支是它的一个连通子图,如下图,G有三个连通分支H1,H2,H3
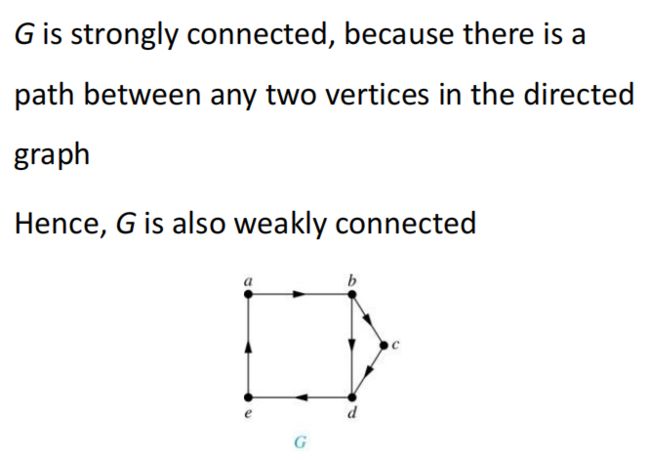
(3)强连通和弱连通
在有向图中,如果有一条边从a指向b,又有一条边从b指向a,那这个有向图称为强连通
如果一个图(不管有无向)里面每两个点之间有一跳路径,那这个图称为弱连通。
弱连通里面包含强连通,因为只要两点之间有路径就行,不用双向边
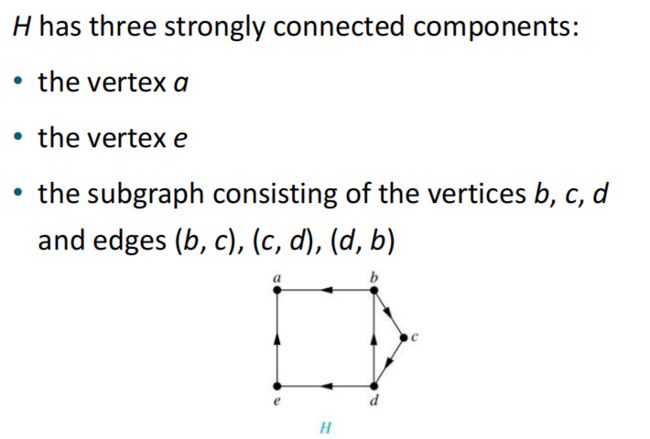
有向图G的子图是强连通的,但不包含在较大的强连通子图中,它们被称为强连通分支或G的强分量。强连通分支也可以是一个点,比如下面的例子
这里的a和e,无论再加什么点也没办法使(a,b,d,e)变成强连通分支,又因为b和d两个顶点被并到(b,d,e)里面了,所以遗留在外面的a和e自己成为一个强连通分支。
3. 割割割
(1)割点
有时,在一个图中把一个顶点和其所有入射边移除,会产生一个具有更多连通分支的子图,这样的点就叫做割点
(2)割边
如果把一条边割掉会产生更多连通分支的图,这条边就叫做割边
(3)不可分割图
没有割点的连通图被称为不可分割图,它比普通的连通图更加连通
(4)点割集(vertex cut):割点组成的集合
(5)点连通度(Vertex Connectivity)
删除多少点后,图不连通?
在n个点的图中0≤k(G)≤n-1
无向完全图点连通度:k(G)=n-1
平凡图(不连通图)点连通度为0.(平凡图只有一个顶点,无边)
比如G1这幅图,我们删除c或者e就能使这个图不连通,也就是说最小割点数量是1,k(G1) = 1
k连通(k(G)≥k)
如果图G是1-连通的(k=1),它是1连通的;如果图是2-连通的(k=2),它是不可分的
(6)边连通度 (Edge Connectivity)
删除最少多少边后,图不连通
在n个点的图中,0≤![]() (G)≤n-1
(G)≤n-1
当图不连通时,λ(G) = 0
图是完全图时λ(G) = n - 1
还是刚刚的G1
在这个图里面我们只用去掉ce这一条边是就能使图不连通,所以λ(G1) = 1
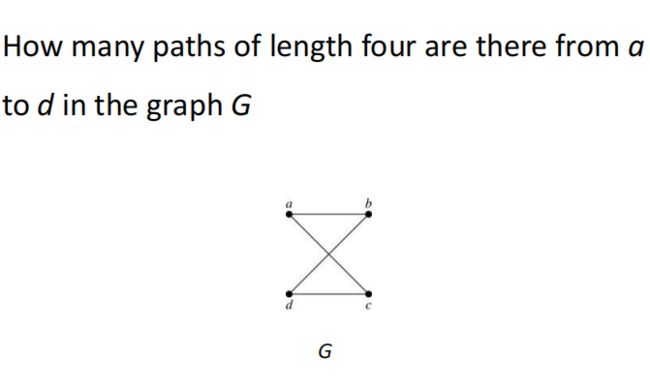
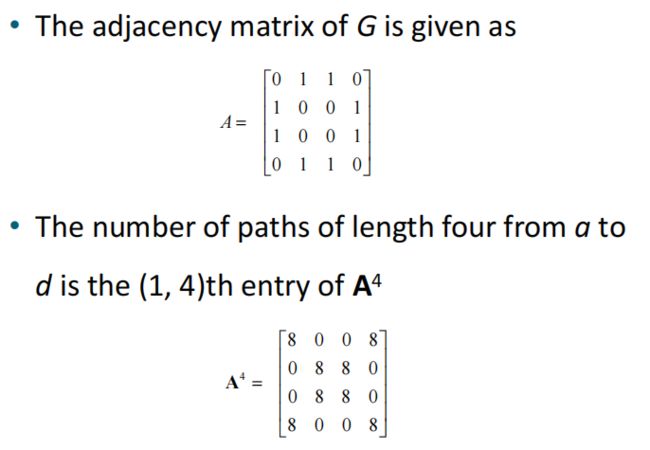
4.计算顶点之间的路径数量
设G是一个具有邻接矩阵A的图,有v1,v2,....vn这些顶点
长度为r的从vi到vj的不同路径的数量等于A^r