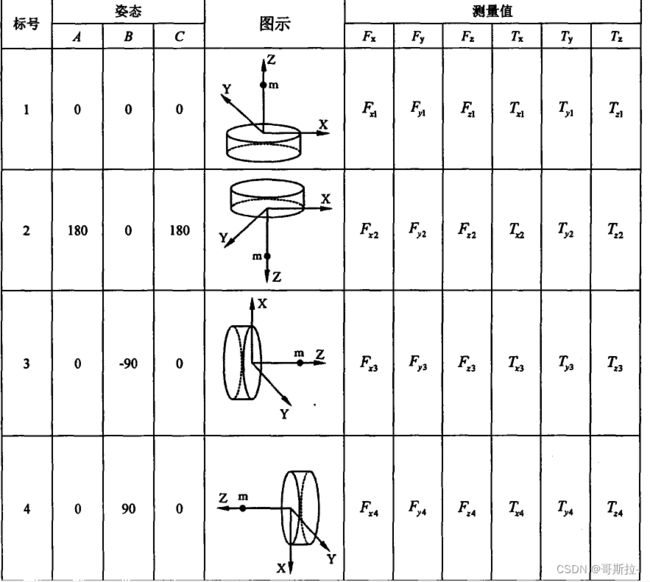
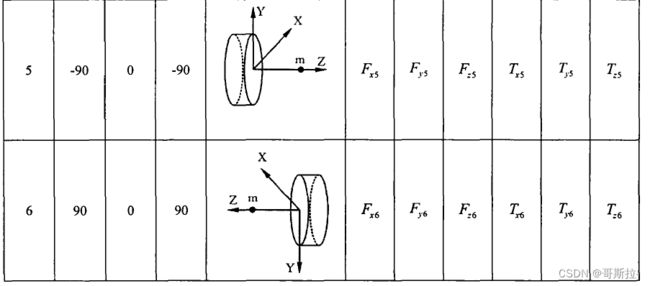
末端工具重力辨识

辨识工具重力

法一：6点标定

已知，工件重力在世界坐标系的大小为$\{0,0,-G\}$,假设工件重心在工具坐标系下的坐标为 $\{L_x,L_y,L_z\}$，重力在工件的三个坐标轴分量为 $\{G_x,G_y,G_z\}$,重力矩在三个坐标轴的分量为$\{M_x,M_y,M_z\}$

根据力和力矩关系：
$$\{\begin{array}{l}{M}_x=G_z\ast L_y-G_y\ast L_z\\ M_y=G_x\ast L_z-G_z\ast L_x\\ M_z=G_y\ast L_x-G_x\ast L_y\end{array}\text{\hspace{1em}(1)}$$
求重力 $G$ 与质心数据 $\{L_x,L_y,L_z\}$，先测量力传感器处于这几个姿态下的力传感器读数：

计算质量数据和质心数据：

$G=\frac{F_{z2}-F_{z1}+F_{x4}-F_{x3}+F_{y6}-F_{y5}}{6}$

$L_x=\frac{T_{y1}-T_{y2}+T_{z6}-T_{z5}}{4G}$

$L_y=\frac{T_{x2}-T_{x1}+T_{z3}-T_{z4}}{4G}$

$L_z=\frac{T_{y4}-T_{y3}+T_{x5}-T_{x6}}{4G}$

法二：最小二乘参数辨识

将式一写成矩阵的形式

[ M x M y M z ] = [ 0 F z − F y − F z 0 F x F y − F x 0 ] [ x y z ] \begin{bmatrix} M_x \\ M_y\\M_z \end{bmatrix}=\begin{bmatrix} 0& F_z& -F_y \\ -F_z& 0& F_x\\F_y&-F_x&0\\\end{bmatrix}\begin{bmatrix} x \\ y\\z \end{bmatrix} ​Mx​My​Mz​​ ​= ​0−Fz​Fy​​Fz​0−Fx​​−Fy​Fx​0​ ​ ​xyz​ ​

控制机器人变换末端姿态,取N个不同的负载姿态,为了避免矩阵奇异，至少要求有三个姿态下机器人末端的指向向量不共面，且尽量不接近共面。根据N组传感器数据可得：

[ M x 1 M y 1 M z 1 M x 2 M y 2 M z 2 . . . M x N M y N M z N ] = [ 0 F z 1 − F y 1 − F z 1 0 F x 1 F y 1 F x 1 0 0 F z 2 − F y 2 − F z 2 0 F x 2 F y 2 − F x 2 0 . . . . . . . . . 0 F z N − F y N − F z N 0 F x N F y N − F x N 0 ] [ x y z ] \begin{bmatrix} M_{x1} \\ M_{y1}\\M_{z1}\\ M_{x2} \\ M_{y2}\\M_{z2}\\ .\\.\\.\\M_{xN} \\ M_{yN}\\M_{zN}\\ \end{bmatrix}=\begin{bmatrix} 0& F_{z1}& -F_{y1} \\ -F_{z1}& 0& F_{x1}\\F_{y1}&F_{x1}&0\\ 0& F_{z2}& -F_{y2} \\ -F_{z2}& 0& F_{x2}\\F_{y2}&-F_{x2}&0\\ .&.&.\\ .&.&.\\ .&.&.\\ 0& F_{zN}& -F_{yN} \\ -F_{zN}& 0& F_{xN}\\F_{yN}&-F_{xN}&0\\ \end{bmatrix}\begin{bmatrix} x \\ y\\z \end{bmatrix} ​Mx1​My1​Mz1​Mx2​My2​Mz2​...MxN​MyN​MzN​​ ​= ​0−Fz1​Fy1​0−Fz2​Fy2​...0−FzN​FyN​​Fz1​0Fx1​Fz2​0−Fx2​...FzN​0−FxN​​−Fy1​Fx1​0−Fy2​Fx2​0...−FyN​FxN​0​ ​ ​xyz​ ​
即
$$\mathbf{m}=F\mathbf{p}$$
由伪逆得：
$$\mathbf{p}=(F^{T}F{)}^{-1}{F}^T\mathbf{m}$$

两种方法在实际情况不太好实现，即使调零了，变换一下方向六维力传感器的读数也会变化，在工具不重的情况下影响很大，所以最好每个使用的位姿，都调一下零，或者知道六维力传感器的初始读数。

如何对末端工具进行补偿

已知工具重力在base坐标系(b)下的方向为 ${}^b{P}_g=\{0;0;-G\}$,在工具坐标系（t）中的坐标为 $L=\{0;0;l_Z\}$, 求 $G_x,G_y,G_z,T_{gx},T_{gy},T_{gz}$

则在工具坐标系下，重力的方向为：

$${}^{t}P{=}_b^{t}R{\cdot }^b{P}_g$$

力矩大小为：
$$n=L{\times }^{t}P$$

参考文献,
[1]张立建,胡瑞钦,易旺民.基于六维力传感器的工业机器人末端负载受力感知研究[J].自动化学报,2017,43(03):439-447.DOI:10.16383/j.aas.2017.c150753.
[2]赵敏. 装配机器人作业过程控制系统应用与软件开发[D].东南大学,2016.