统计学中的「标准差和方差」

标准差(Standard deviation)

简单来说，标准差是一组数值自平均值分散程度的一种测量观念。一个较大的标准差，代表大部分的数值和其平均值之间差异较大，一个较小的标准差，代表这些数值较接近平均值。
 

例如：

两组数的集合 {0， 5， 9， 14} 和 {5， 6， 8， 9} 其平均值都是7，但第二个集合具有较小的标准差

• 标准差公式：

• 公式描述：公式中数值为X1,X2,X3,……XN（皆为实数），其平均值（算数平均值）μ，标准差为σ

标准差可以当作不确定性的一种测量。在物理科学中，做重复性测量时，测量数值集合的标准差代表这些测量的精确度。当要决定测量值是否符合预测值，测量值的标准差占有决定性重要角色。如果测量平均值与预测值相差太远(同时与标准差数值做比较)，则认为测量值与预测值互相矛盾。这很容易理解，因为如果测量值都落在一定数值范围之外，可以合理推论预测值是否正确。

标准差应用于投资上，可作为量度回报稳定性的指标。标准差数值越大，代表回报远离过去平均数值，回报较不稳定故风险越高。相反，标准差数值越小，代表回报较为稳定，风险亦较小。
 

例如：

A，B两组各有6位学生参加同一次语文测验，A组的分数为95，85，75，65，55，45　　

B组的分数为73，72，71，69，68，67

 

这两组的平均数都是70，但A组的标准差为17.078分，B组的标准差为2.160分，说明A组学生之间的差距要比B组学生之间的差距大得多

方差(variance)

两人的5次测验成绩如下：

A：50，100，100，60，50　　-->Average(A) = 72

B：73，70，75，72，70　　    -->Average(B) = 72
 

平均成绩相同，但A不稳定，对平均值偏大

方差描述随机变量对于数学期望的偏离程度

• 方差公式：

• 公式描述：公式中x为平均数，n为这组数据个数，x1,x2,x3……xn为这组数据具体数值。

可以看到方差是标准差的平方

除了期望，方差(variance)是另一个常见的分布描述量。如果说期望表示的是分布的中心位置，那么方差就是分布的离散程度。方差越大，说明随机变量取值越离散。

比如射箭时，一个优秀的选手能保持自己的弓箭集中于目标点附近，而一个经验不足的选手，他弓箭的落点会更容易散落许多地方。

上面的靶上有两套落点。尽管两套落点的平均中心位置都在原点 (即期望相同），但两套落点的离散程度明显有区别。蓝色的点离散程度更小。

数学上，我们用方差来代表一组数据或者某个概率分布的离散程度。可见，方差是独立于期望的另一个对分布的度量。两个分布，完全可能有相同的期望，而方差不同，正如我们上面的箭靶。

对于一个随机变量XX来说，它的方差为：Var(X)=E[(X−μ)2]Var(X)=E[(X−μ)2]

其中，μμ表示XX的期望值，即μ=E(X)μ=E(X)

我们可以代入期望的数学表达形式。

比如连续随机变量：Var(X)=E[(X−μ)2]=∫+∞−∞(x−μ)2f(x)dxVar(X)=E[(X−μ)2]=∫−∞+∞(x−μ)2f(x)dx
 

方差概念背后的逻辑很简单：一个取值与期望值的“距离”用两者差的平方表示。该平方值表示取值与分布中心的偏差程度，平方的最小取值为0，当取值与期望值相同时，此时不离散，平方为0，即“距离”最小；当随机变量偏离期望值时，平方增大。由于取值是随机的，不同取值的概率不同，我们根据概率对该平方进行加权平均，也就获得整体的离散程度——方差。

方差的平方根称为标准差(standard deviation， 简写std)。我们常用σσ表示标准差。σ=Var(X)−−−−−−√σ=Var(X)

标准差也表示分布的离散程度。

 正态分布的方差 

根据上面的定义，可以算出正态分布：

E(X)=1σ2π−−√∫+∞−∞xe−(x−μ)2/2σ2dxE(X)=1σ2π∫−∞+∞xe−(x−μ)2/2σ2dx的

方差为：Var(X)=σ2Var(X)=σ2
 

正态分布的标准差正等于正态分布中的参数σσ。这正是我们使用字母σσ来表示标准差的原因！

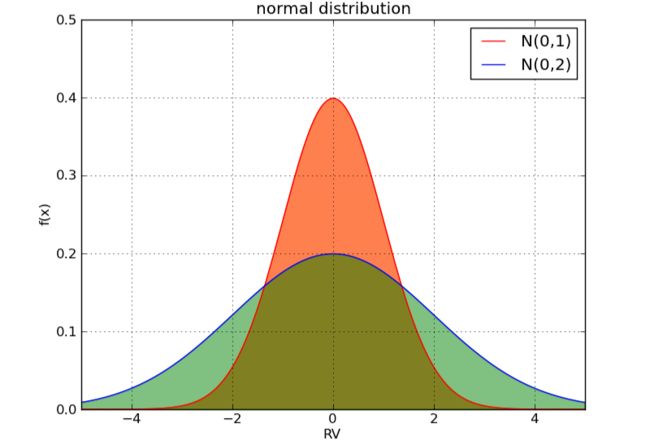
可以预期到，正态分布的σσ越大，分布离散越大，正如我们从下面的分布曲线中看到的：

当方差小时，曲线下的面积更加集中于期望值0附近。当方差大时，随机变量更加离散。此时分布曲线的“尾部”很厚，即使在取值很偏离0时，比如x=4x=4时，依然有很大的概率可以取到。

代码如下:

# 

from scipy.stats import normimport numpy as npimport matplotlib.pyplot as plt

# Note the difference in "scale"， which is stdrv1 = norm(loc=0， scale = 1)rv2 = norm(loc=0， scale = 2)

x = np.linspace(-5， 5， 200)

plt.fill_between(x， rv1.pdf(x)， y2=0.0， color="coral")plt.fill_between(x， rv2.pdf(x)， y2=0.0， color="green"， alpha = 0.5)

plt.plot(x， rv1.pdf(x)， color="red"， label="N(0，1)")plt.plot(x， rv2.pdf(x)， color="blue"， label="N(0，2)")

plt.legend()plt.grid(True)

plt.xlim([-5， 5])plt.ylim([-0.0， 0.5])

plt.title("normal distribution")plt.xlabel("RV")plt.ylabel("f(x)")

plt.show()

 指数分布的方差 

指数分布的表达式为：f(x)={λe−λx0ififx≥0x<0f(x)={λe−λxifx≥00ifx<0
 

它的方差为：Var(X)=1λ2Var(X)=1λ2
 

如下图所示：
 

 Chebyshev不等式 

我们一直在强调，标准差(和方差)表示分布的离散程度。标准差越大，随机变量取值偏离平均值的可能性越大。如何定量的说明这一点呢？我们可以计算一个随机变量与期望偏离超过某个量的可能性。比如偏离超过2个标准差的可能性。即P(|X−μ|>2σ)P(|X−μ|>2σ)

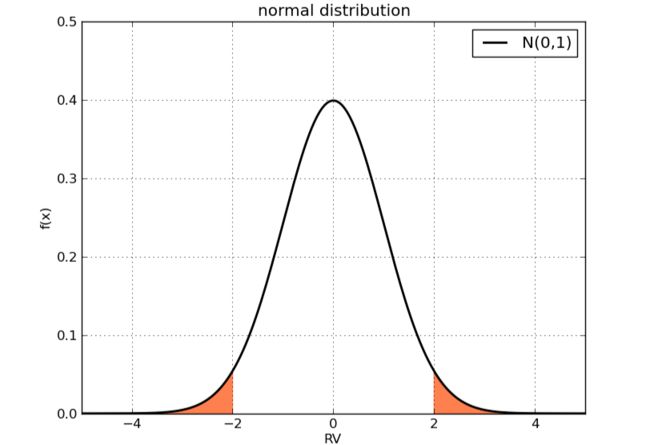
这个概率依赖于分布本身的类型。比如正态分布N(0，1)N(0，1)，这一概率即为x大于2，或者x小于-2的部分对应的曲线下面积：

实际上，无论μμ和σσ如何取值，对于正态分布来说，偏离期望超过两个标准差的概率都相同，约等于0.0455 (可以根据正态分布的表达式计算)。随机变量的取值有约95.545%的可能性落在正负两个标准差的区间内，即从-2到2。如果我们放大区间，比如正负三个标准差，这一概率超过99%。我们可以相当有把握的说，随机变量会落正负三个标准差之内。上面的论述并不依赖于标准差的具体值。这里可以看到标准差所衡量的“离散”的真正含义：如果取相同概率的极端值区间，比如上面的0.0455，标准差越大，该极端值区间距离中心值越远。

然而，上面的计算和表述依赖于分布的类型（正态分布）。如何将相似的方差含义套用在其它随机变量身上呢？

Chebyshev不等式让我们摆脱了对分布类型的依赖。它的叙述如下：

• 对于任意随机变量X，如果它的期望为μμ，方差为σ2σ2，那么对于任意t>0t>0，P(|X−μ|>t)≤σ2tP(|X−μ|>t)≤σ2t

• 无论X是什么分布，上述不等式成立。我们让t=2σt=2σ，那么P(|X−μ|>2σ)≤0.25P(|X−μ|>2σ)≤0.25

也就是说，X的取值超过两个正负标准差的可能性最多为25%。换句话说，随机变量至少有75%的概率落在正负两个标准差的范围内。（显然这是最“坏”的情况下。正态分布显然不是”最坏“的）

from scipy.stats import normimport numpy as npimport matplotlib.pyplot as plt

# Note the difference in "scale"， which is stdrv1 = norm(loc=0， scale = 1)

x1 = np.linspace(-5， -1， 100)x2 = np.linspace(1， 5， 100)x = np.linspace(-5， 5， 200)plt.fill_between(x1， rv1.pdf(x1)， y2=0.0， color="coral")plt.fill_between(x2， rv1.pdf(x2)， y2=0.0， color="coral")plt.plot(x， rv1.pdf(x)， color="black"， linewidth=2.0， label="N(0，1)")

plt.legend()plt.grid(True)

plt.xlim([-5， 5])plt.ylim([-0.0， 0.5])

plt.title("normal distribution")plt.xlabel("RV")plt.ylabel("f(x)")

plt.show()

MAD绝对中位值

中位数：统计学名词，是指将统计总体中的各个变量值按大小顺序排列起来形成一个数列，处于变量数列中间位置的变量值就称为中位数。

MAD：就是先求出给定数据的中位数(注意并非均值)然后原数列的每个值与这个中位数求出绝对差，然后新数列的中位值就是MAD

例如：

数据A：8，5，9，6，3，2，4，9　　2，3，4，5，6，8，9

中位数 = 5

A - 5 = 3，0，4，1，2，3，1，4　　0，1，1，2，3，3，4

MAD = 2

总 结

• 标准差为方差的平方根

• 方差用于表示分布的离散程度，方差越大，“极端区间”偏离中心越远