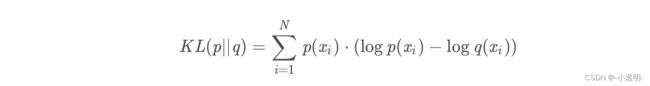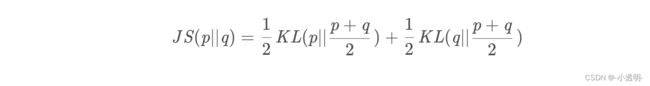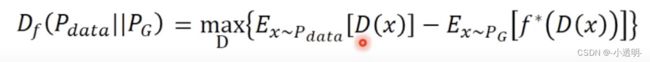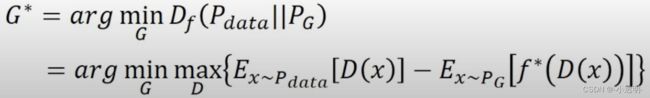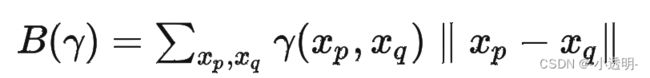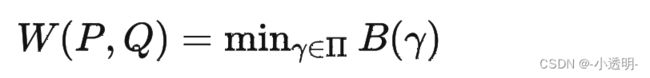图像生成--对抗生成模型

生成模型概述

对抗生成模型

机器学习中的两大主要问题：

1. 判别
2. 生成

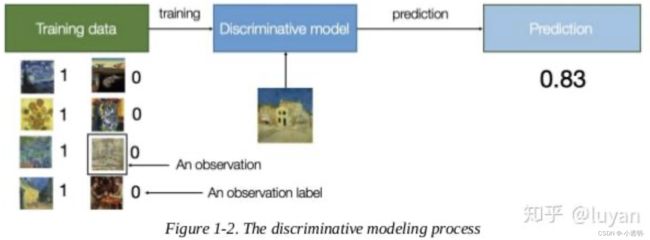
判别模型的典型代表即为图像分类任务，即给定一个数据，判定他是哪一类。

判别模型学习到的是一个概率（贝叶斯过程）

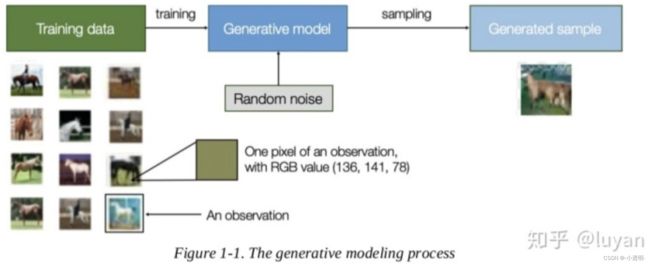
而生成模型的区别在于，给定一个数据，将其生成为预期数据。

 

在数学上，生成模型与判别模型的区别在于：

给定观测值x：

• 判别模型旨在判别得到y的概率

• 生成模型旨在根据指定的y得到x的概率

生成模型的应用

超分辨率

图像生成(风格迁移)

生成模型原理简要说明

在GoodFellow的论文中，以最大似然估计进行举例。

首先需要说明的问题是：

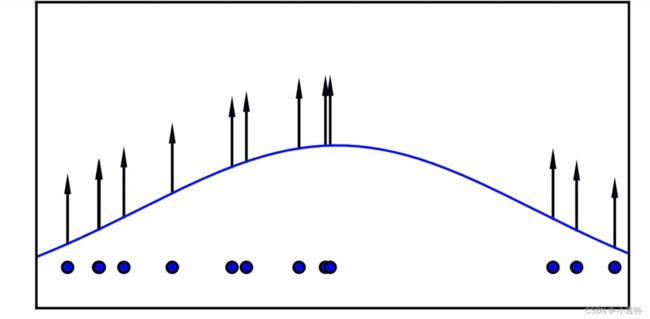
生成模型的本质，在于从训练数据中学习到数据的分布

学习到了分布之后，给定一个随机的噪声。

过程可以简单地理解为：这个噪声中，符合指定分布的内容得到加强，不符合指定分布的内容会被削弱。

当在迭代过程中，数据逐渐贴合预期的输入，从而看上去更逼真。

方法分类

基于最大似然估计的数据生成，是生成模型的理论基础。

按照不同的形式和流派，大致可以分成下面的类别。

此处不对研究脉络的具体细节进行探究，只是对原理进行比喻式介绍。

1. Explicit density： 显性密度。也就是说，我们在这类方法中，需要给出分布模型的具体形式（密度函数），通过各种迭代运算，来得到模型的真实参数。

2. Implicit density：隐性密度。在这类方法中，不指定数据分布密度函数，而是通过数据分布所满足的条件，用拟合能力比较强的模型来寻找合适的模型和分布参数。

而GAN则属于隐式密度方法，不需要指定模型的具体分布密度函数，来得到较好的分布拟合。

拓展：生成模型可以视为一种损失函数

该部分内容会在后续进行进一步展开，此处只做简单介绍。

首先，我们通常会采用显式的函数作为损失函数。

这种方式带来很多便利，但并不一定精确(对特定任务来说)。

我们用对抗生成式的模型对网络进行约束，从而能够不使用显性的函数来约束模型。

对于用于约束的网络，我们将一些必须要满足的条件作为约束目标，从而令约束模型进一步地摸索出更好的约束边界。

生成对抗模型GAN

Generative Adversarial Network，GAN是一种深度学习模型，属于一种无监督学习的方法。

其目的在于，从数据中学习分布，来得到足以以假乱成真的数据。

为了达到这个目的，通常包含两个基本模型：生成器和判别器。(generative model, G)和(discriminative model, D)

判别模型学习“分界面（分解曲线）”

在训练过程中，利用合理的结构和设定，令二者满足纳什均衡，来得到最优解。

GAN原理

GAN的过程，离不开两个关键内容：生成与对抗。

Goodfellow的例子如下：

一个城市中，有一群小偷(生成器)和一群警察（判别器）。

小偷的目的在于，想方设法地欺骗警察；

而警察的目的在于，想方设法地不受欺骗。

这样一来，小偷在不断的欺骗和被识破的过程中不断精进技能，从而掌握了更加不易被识破的欺骗技能；

警察则在被欺骗的过程中，不断提高辨识功能，从而对欺骗的细节做出判断，更加接近本质。

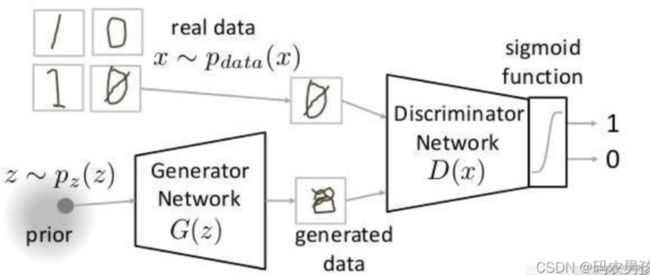
生成器 生成器采用随机输入，尝试输出样本数据。根据输入的样本随机产生一个数据，将其送入鉴别器

鉴别器 鉴别器的任务在于，接受两个输入，分别是生成器的输入和真实数据，判别器的目的在于判断生成器的输入是不是真的。

数学表达

上述过程中，希望判别器能够最大程度地判别出真实数据为真，生成数据为假。

而生成器则是能够最大程度地令判别器产生误判。

训练过程

两阶段训练：

1. 固定生成器参数，训练判别器

2. 固定判别器，训练生成器

GAN模型的训练过程是一个非常复杂的训练过程，早期的GAN训练也非常麻烦。

训练难度之所以大，一个重要的原因在于，难以掌控生成器和判别器的能力。

理解：

如果小偷很厉害，则警察无法从中提升判别能力；

如果警察很厉害，小偷则会被一网打尽，无法提升其“造假能力”

理论上，如果判别器过于强大，生成器则会由于步长太大无法找到全局最优解。

一个简单的例子在于，人类现代科技无法从外星人科技中吸收影响，从而无法引发科技进步。

因此，通常是训练多轮生成器，再训练少轮判别器。

通俗来说，GAN训练的过程应当是一个循序渐进，相辅相成的过程。如果一开始，通过载入与训练模型令判别器具有很高的能力，往往会令GAN难以有效收敛。

代码实践

参考

In [1]:

import torch
import torchvision
import torch.nn as nn
from torchvision import transforms
from tqdm import tqdm

In [2]:

transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize(.5, .5)
])
train_data = torchvision.datasets.MNIST('data', 
                                        train=True,
                                        transform=transform,
                                        download=True)

dataloader = torch.utils.data.DataLoader(train_data, batch_size=64, shuffle=True)
Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz to data/MNIST/raw/train-images-idx3-ubyte.gz

  0%|          | 0/9912422 [00:00 
  
Extracting data/MNIST/raw/train-images-idx3-ubyte.gz to data/MNIST/raw

Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz to data/MNIST/raw/train-labels-idx1-ubyte.gz
 
  
  0%|          | 0/28881 [00:00 
  
Extracting data/MNIST/raw/train-labels-idx1-ubyte.gz to data/MNIST/raw

Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz to data/MNIST/raw/t10k-images-idx3-ubyte.gz
 
  
  0%|          | 0/1648877 [00:00 
  
Extracting data/MNIST/raw/t10k-images-idx3-ubyte.gz to data/MNIST/raw

Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz to data/MNIST/raw/t10k-labels-idx1-ubyte.gz
 
  
  0%|          | 0/4542 [00:00 
  
Extracting data/MNIST/raw/t10k-labels-idx1-ubyte.gz to data/MNIST/raw

 
  
In [3]:
 
  
# generator
class Gen(nn.Module):
    def __init__(self):
        super(Gen, self).__init__()
        self.gen = nn.Sequential(nn.Linear(100, 256), 
                                 nn.ReLU(),
                                 nn.Linear(256, 512), 
                                 nn.ReLU(), 
                                 nn.Linear(512, 28*28), 
                                 nn.Tanh())
    
    def forward(self, x):
        img = self.gen(x)
        img = img.view(-1, 28, 28)
        return img
 
  
In [4]:
 
  
# discriminator
class Dis(nn.Module):
    def __init__(self):
        super(Dis, self).__init__()
        self.dis = nn.Sequential(nn.Linear(28*28, 512), 
                                 nn.LeakyReLU(),
                                 nn.Linear(512, 256), 
                                 nn.LeakyReLU(), 
                                 nn.Linear(256, 1),
                                 nn.Sigmoid())
    
    def forward(self, x):
        x = x.view(-1, 28*28)
        x = self.dis(x)
        return x
 
  
In [5]:
 
  
gen = Gen().to('cpu')
dis = Dis().to('cpu')

d_optim = torch.optim.Adam(dis.parameters(), lr=1e-4)
g_optim = torch.optim.Adam(gen.parameters(), lr=1e-4)

loss_func = torch.nn.BCELoss()
 
  
In [6]:
 
  
# train
loss_d = []
loss_g = []

for epoch in range(50):
    d_epoch_loss = 0
    g_epoch_loss = 0
    batch_count = len(dataloader)
    
    for i, (img, _) in enumerate(tqdm(dataloader)):
        img = img.to('cpu')
        size = img.size(0)
        random_noise = torch.randn(size, 100, device='cpu')
        
        d_opt.zero_grad()
        real_output = dis(img)
        d_real_loss = loss_func(real_output, 
                                torch.ones_like(real_output))
        d_real_loss.backward()
        
        gen_img = gen(random_noise)
        fake_output = dis(gen_img.detach())
        d_fake_loss = loss_func(fake_output, 
                                torch.zeros_like(fake_output))
        d_fake_loss.backward()
        
        d_loss = d_real_loss + d_fake_loss
        d_optim.step()
        
        g_optim.zero_grad()
        fake_output = dis(gen_img)
        g_loss = loss_func(fake_output, 
                           torch.ones_like(fake_output))
        
        g_loss.backward()
        g_optim.step()
    
        torch.save(gen.state_dict(), str(epoch).zfill(2) + ".pth")
 
  
100%|█████████████████████████████████████████| 938/938 [00:22<00:00, 42.29it/s]
100%|█████████████████████████████████████████| 938/938 [00:22<00:00, 42.55it/s]
100%|█████████████████████████████████████████| 938/938 [00:22<00:00, 42.48it/s]
100%|█████████████████████████████████████████| 938/938 [00:22<00:00, 42.15it/s]
 57%|███████████████████████▍                 | 537/938 [00:12<00:09, 41.52it/s]
 
  
---------------------------------------------------------------------------
 
  
In [7]:
 
  
# show result
def result_show(weight, test_input):
    gen = Gen().to('cpu')
    gen.load_state_dict(torch.load(weight))
    gen.eval()
    plot_img(gen, test_input)
 
  
In [8]:
 
  
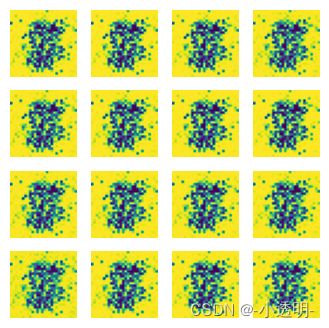
# plot image
import matplotlib.pyplot as plt

def plot_img(model, _input):
    prediction = model(_input).detach().cpu().numpy()
    print(prediction.shape)
    fig = plt.figure(figsize=(4, 4))
    for i in range(16):
        plt.subplot(4, 4, i+1)
        plt.imshow((prediction[i]+1)/2)
        plt.axis('off')
    plt.show()
 
  
In [9]:
 
  
random_noise = torch.randn(size, 100)
import numpy as np

result_show('./00.pth', random_noise)
 
  
(64, 28, 28)
 
  
 
  
GAN模型进阶
 
  
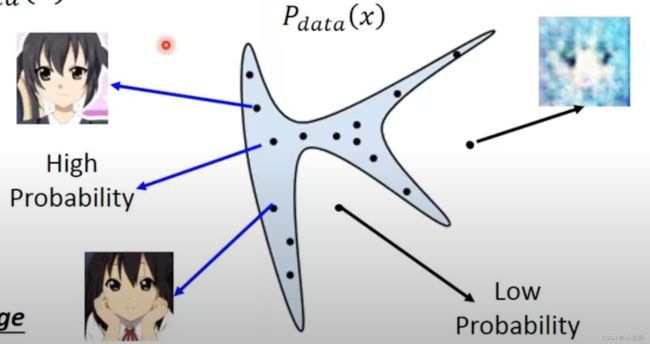
GAN模型的本质
 
  
 
  
学习训练数据的分布，符合训练数据分布的数据，具有较好的可视化效果；
 
  
在分布之外的数据，可视化效果较差。
 
  
那么GAN模型的根本问题是：
 
  
找一个生成模型G，该模型定义了概率分布
 
  
 
  
给定一个分布z，找到一个G，可以使分布比较相似。
 
  
 
  
 具体上，从符合z分布中采样多个点，得到了多个x。
 
  
进而，从创造一个D，用于引导采样。
 
  
 
  
需要说明的是，D的loss值与生成数据和真实数据的内容息息相关。
 
  
如果说损失越大，则越说明生成的数据和真实数据越接近。
 
  
一个直观的例子
 
  
 
  
李宏毅推荐的例子
 
  
 
  
GAN的本质：散度
 
  
散度定义（divergence）：p(x)和q(x)到底有多不一样
 
  
 
  
性质1: 散度取值在0-1之间，越接近于0，分布越相似。否则分布区别越大。
 
  
那么GAN的本质，在于如何度量散度，即如何设定一个合适的函数f，来得到一个良好的分布拟合。
 
  
 
  
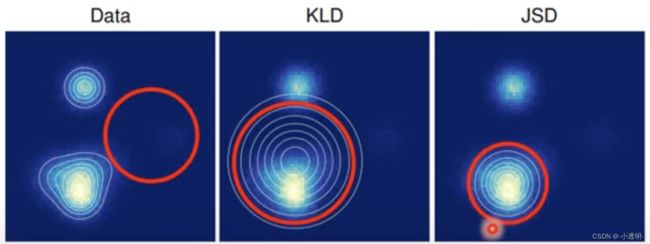
KL散度：描述数据分布之间的相似性
 
  
卡方散度：判断两个样本是否符合相同的分布
 
  
关于散度和GAN的关系
 
  
散度用于评价分布的相似程度。
 
  
常用的KL散度，公式为
 
  
 
  
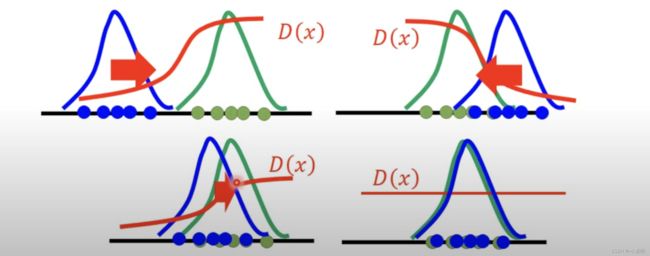
但KL散度存在不对称性，在basic gan里，用的是JS散度
 
  
 
  
使用JS散度存在一个比较大的问题，即如果分布相差较远，则会等于一个恒定的值。不利于模型收敛。
 
  
 
  
因此，可以灵活地调整散度，来适应不同类型的数据。
 
  
 
  
如何把散度作为优化目标？
 
  
散度可以衡量两个分布，那么如何将散度作为他的优化函数呢？
 
  
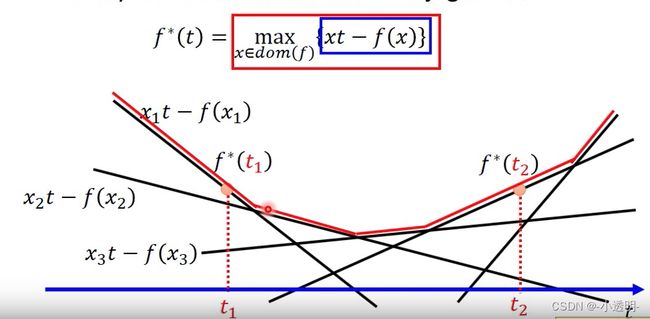
凸共轭
 
  
 
  
 
 
  
 
  
红线部分即共轭函数的曲线，可以看出他也是凸函数。
 
  
如何求解一个函数的凸函数？
 
  
采用极值求导的方式求解。
 
  
例如f(x)=xlog⁡x
 
  
一般形式的GAN
 
  
 
  
回到GAN中，有
 
  
 
  
那么我们的目的就在于：
 
  
 
  
直观上的感受：
 
  
 
  
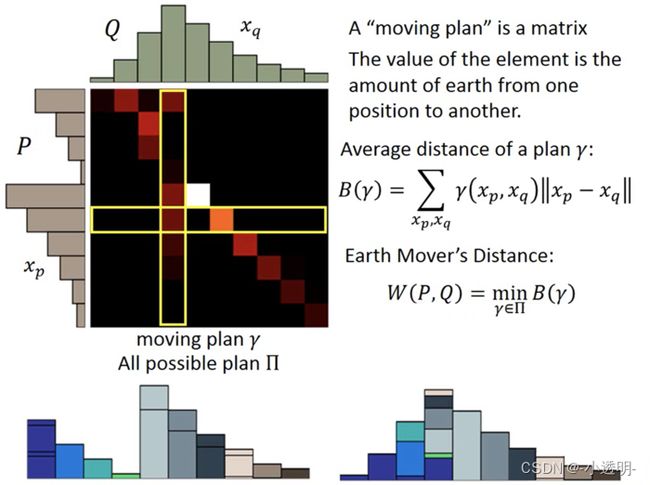
另一种思路 WGAN
 
  
 
  
有颜色的色块表示把第i行的分布，修改到第j行。(推土机)
 
  
运送路径越多，运送的货物越多，则做的功越大。
 
  
那么首先定义运送的功
 
  
 
  
进而，只需要找到运送功最小的那个方案就可以了
 
  
 
  
 
  
 
  
注意，这里需要定义D的函数需要满足1-Lipschitz，即
 
  
 
  
其中，k=1
 
  
这样的作用在于，令y的增长不超过x。也就是限制模型不要更新的太快。
 
  
否则，如果取消限制，那么就会令D直接爆炸。
 
  
求解