二叉搜索树之AVL树

目录

1.概念

2.定义

3.插入

4.旋转

1. 新节点插入较高左子树的左侧---右单旋

2. 新节点插入较高右子树的右侧---左单旋

3. 新节点插入较高左子树的右侧：先左单旋再右单旋【左右双旋】

4. 新节点插入较高右子树的左侧---右左：先右单旋再左单旋【右左双旋】

5.验证

6.删除

7.性能分析

---

1.概念

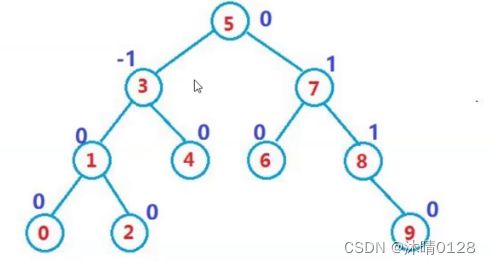
高度平衡的二叉搜索树

一颗AVL树或者是空树,或者是具有以下性质的二叉搜索树 (中序遍历是递增的):

1.左右树都是AVL树

2.左右子树高度之差的绝对值不超过1(-1/0/1)

2.定义

孩子双亲表示法

 static class TreeNode{
        public int val;
        public int bf;
        public Tree left;
        public Tree right;
        public Tree parent;
        public TreeNode(int val){
            this.val=val;
        }
    }

3.插入

1.把数据插入到AVL树当中(和二叉搜索树一样)

1. 为空-->直接插入
2. parent:父节点 cur:当前结点
3. 遍历直到为null
   1. cur.val小,parent=cur,cur指向右结点
   2. 相等,return false-->已经有不用插入
   3. cur.val大,parent=cur,cur指向左结点
4. cur==null 插入结点(此时parent为叶子结点)
   1. parent.val插入parent的右边
   2. parent.val>val -->插入parent的左边

2,插入后,根据平衡因子对树调整

1. 先看cur是parent的左还是右,决定平衡因子是++,还是--
   1. 如果是右树,右树高度++,平衡因子++
   2. 如果是左树,左树高,平衡因子--
2. 检查平衡
   1. 0代表整棵树平衡-->break;
   2. 1和-1表示当前平衡,不保证整棵树平衡,-->向上调整
   3. 2或者-2,当前不平衡
      1. bf==2-->右树高,左旋
      2. bf==-2-->左树高,右旋

public boolean insert(int val){
      TreeNode node=new TreeNode(val);
      if(root==null){
          root=node;
          return true;
      }
      
      TreeNode parent=null;
      TreeNode cur=root;
      while (cur!=null){
          if(cur.val

4.旋转

1.如果在一棵原本是平衡的AVL树中插入一个新节点，可能造成不平衡，此时必须调整树的结构，使之平衡化。根据节点插入位置的不同，AVL树的旋转分为四种：

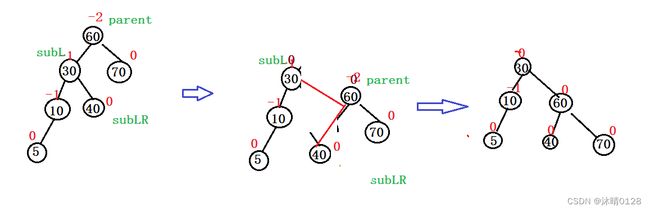
1. 新节点插入较高左子树的左侧---右单旋

 

1.定义结点   subL   subLR

2.改变指向     parent指向subLR    subL指向parent   subLR指向parent

3.如果把subL提起来,要把subL的parent改为parent的parent

4.调整parent和上面的结点,判断parent是否是根节点

        1.如果是,subL变为根节点  root.parent为null

        2.如果是parent是pparent的左子树,subL改为pparent的左子树

        3.如果是parent是pparent的右子树,subL改为pparent的右子树

        4.subL指向pparent

4.平衡因子变为0

 private void rotateRight(TreeNode parent) {
        TreeNode subL=parent.left;
        TreeNode subLR=subL.right;
        //改变指向
        parent.left=subLR;
        subL.right=parent;

        if(subLR!=null){
            subLR.parent=parent;
        }
        //调整parent和上面的结点
        TreeNode pparent=parent.parent;
        parent.parent=subL;

        if(parent==root){
            root=subL;
            root.parent=null;

        }else{
            if(pparent.right==parent){
                pparent.right=subL;
            }else{
                pparent.left=subL;
            }
            subL.parent=pparent;
        }
        //调整平衡因子
        subL.bf=0;
        parent.bf=0;
    }

2. 新节点插入较高右子树的右侧---左单旋

1.定义结点

2.改变指向

3.如果把subR提起来,要把subR的parent改为parent的parent

4.平衡因子变为0

 

private void rotateLeft(TreeNode parent) {
        TreeNode subR=parent.right;
        TreeNode subRL=subR.left;

        parent.right=subRL;
        subR.left=parent;
        if(subRL!=null){
            subRL.parent=parent;
        }

        TreeNode pparent=parent.parent;
        if(parent==root){
            subR=root;
            root.parent=null;
        }else{
            if(pparent.right==parent){
                pparent.right=subR;
            }else{
                pparent.left=subR;
            }
            subR.parent=pparent;
        }
        subR.bf=0;
        parent.bf=0;
    }

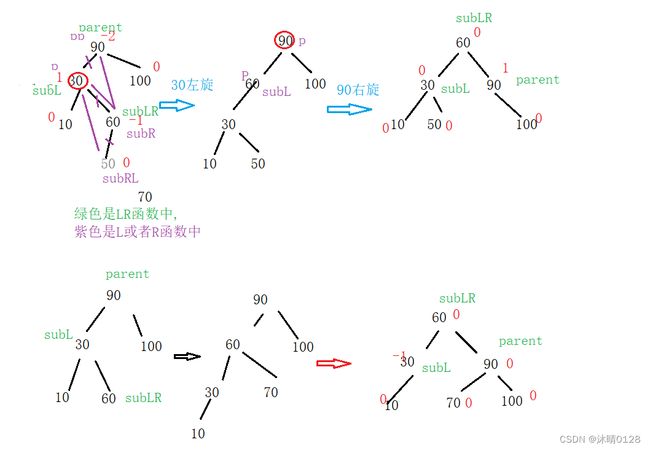
3. 新节点插入较高左子树的右侧：先左单旋再右单旋【左右双旋】

 

因为两种平衡因子的结果不同,所以要区分

1.区分是哪一种情况

2.调用左旋函数

3,调用右旋函数

4.设置平衡因子

 private void rotateLR(TreeNode parent) {
       TreeNode subL=parent.left;
       TreeNode subLR=subL.right;
       int bf=subLR.bf;
       rotateLeft(parent.left);
       rotateRight(parent);
        if(bf==-1){
            subL.bf=0;
            subLR.bf=0;
            parent.bf=1;
        }else if(bf==1){
            subL.bf=-1;
            subLR.bf=0;
            parent.bf=0;
        }

    }

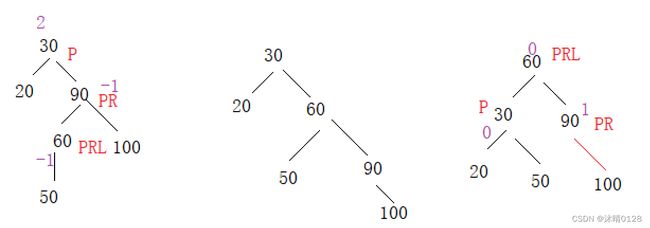
4. 新节点插入较高右子树的左侧---右左：先右单旋再左单旋【右左双旋】

 

private void rotateRL(TreeNode parent) {
        TreeNode subR=parent.right;
        TreeNode subRL=subR.left;
        int bf=subRL.bf;
        rotateRight(parent.right);
        rotateLeft(parent);
        if(bf==-1){
            parent.bf=0;
            subR.bf=1;
            subRL.bf=0;
        }else if(bf==1){//原先新插入的在右边
            parent.bf=-1;
            subR.bf=0;
            subRL.bf=0;
        }

    }

5.验证

1.验证为二叉搜索树

如果中序遍历可得到一个有序的序列，就说明为二叉搜索树

//中序遍历的结果是有序
public void inorder(TreeNode root){
    if(root==null) return;
    inorder(root.left);
    System.out.println(root.val+" ");
    inorder(root.right);
}

2. 验证其为平衡树

• 每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
• 节点的平衡因子是否计算正确

• private int height(TreeNode root){
      if(root==null) return 0;
      int leftH=height(root.left);
      int rightH=height(root.right);
      return leftH > rightH ? leftH+1 : rightH+1;
  }
  
  //判断是否是平衡二叉树
  public boolean isBalanced(TreeNode root){
      if(root==null) return true;
      int leftH=height(root.left);
      int rightH=height(root.right);
  
      if(rightH-leftH !=root.bf){
          System.out.println("这个节点"+root.val+"平衡因子异常");
          return false;
      }
      return Math.abs(leftH-rightH) <=1
              && isBalanced(root.left)
              && isBalanced(root.right);
  
  }

3.验证用例

public static void main(String[] args) {
   int[] array={16,3,7,11,9,26,18,14,15};
    //int[] array={4, 2, 6, 1, 3, 5, 15, 7, 16, 14};
    AVLTree avlTree=new AVLTree();
    for(int i=0;i< array.length;i++){
        avlTree.insert(array[i]);
    }
    System.out.println(avlTree.isBalanced(avlTree.root));
}

6.删除

思路:

1、找到需要删除的节点

2、按照搜索树的删除规则删除节点

3、更新平衡因子，如果出现了不平衡，进行旋转。--单旋，双旋

7.性能分析

如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修改，就不太适合。