论文笔记-Multi-Task Learning as Multi-Objective Optimization

Intro

在深度学习，使用多个任务（loss）训练模型时，通常使用最小化加权线性和的方式来训练整个模型。但是这要求多任务之间不存在相互竞争。因此作者提出新的多任务学习方法，将多任务学习转化成多目标优化问题，借助凸优化问题求帕累托（pareto）最优解。

method

问题定义

对一个输入空间X和任务集合空间${\left\{{\mathcal{Y}}^t\right\}}_{t\in [T]}$上的多任务问题（MSL）进行研究，在数据集中数据点可以表示为${\left\{{\mathbf{x}}_i,y_i^1,\dots ,y_i^T\right\}}_{i\in [N]}$，其中T表示任务数量，N表示数据点个数。每一个任务的表示为$f^t\left(\mathbf{x};{\mathbf{\theta }}^{sh},{\mathbf{\theta }}^t\right):\mathcal{X}\to {\mathcal{Y}}^t$。损失函数表示为${\mathcal{L}}^t(\cdot ,\cdot ):{\mathcal{Y}}^t\times {\mathcal{Y}}^t\to {\mathbb{R}}^{+}$。
多任务的总损失函数通常被表示为：
$$\underset{\begin{array}{c}{\mathbf{\theta }}^{sh},{\mathbf{\theta }}^1,\dots ,{\mathbf{\theta }}^T\end{array}}{\min }\sum _{t=1}^T{c}^t{\hat{\mathcal{L}}}^t\left({\mathbf{\theta }}^{sh},{\mathbf{\theta }}^t\right)$$
对每个任务静态或者动态计算权重$c^t$，其中${\hat{\mathcal{L}}}^t\left({\mathbf{\theta }}^{sh},{\mathbf{\theta }}^t\right)$表示任务t的经验损失（${\hat{\mathcal{L}}}^t\left({\mathbf{\theta }}^{sh},{\mathbf{\theta }}^t\right)\triangleq \frac{1}{N}{\sum }_i\mathcal{L}\left(f^t\left({\mathbf{x}}_i;{\mathbf{\theta }}^{sh},{\mathbf{\theta }}^t\right),y_i^t\right)$）。
加权求和在直观上很吸引人，但是它通常需要在各种规模进行复杂的网格搜索，或者使用启发式算法。
另外，在MTL中不能定义全局最优性。假设两个解决方案$\theta$和$\overline{\theta }$，它们使得${\hat{\mathcal{L}}}^{t_1}\left({\mathbf{\theta }}^{sh},{\mathbf{\theta }}^{t_1}\right)<{\hat{\mathcal{L}}}^{t_1}\left({\overline{\mathbf{\theta }}}^{sh},{\overline{\mathbf{\theta }}}^{t_1}\right)$和${\hat{\mathcal{L}}}^{t_2}\left({\mathbf{\theta }}^{sh},{\mathbf{\theta }}^{t_2}\right)>{\hat{\mathcal{L}}}^{t_2}\left({\overline{\mathbf{\theta }}}^{sh},{\overline{\mathbf{\theta }}}^{t_2}\right)$。也就是说对于任务$t_1$参数$\theta$ 更好，对于任务$t_2$参数$\overline{\theta }$ 更好。如果没有关于两任务重要性的说明，是不能对比两种解决方案即两种参数的优劣。
MTL可以表述为多目标优化，优化一个可能相互冲突的目标集合，使用损失L表示：
$$\underset{\begin{array}{c}{\mathbf{\theta }}^{sh},{\mathbf{\theta }}^1,\dots ,{\mathbf{\theta }}^T\end{array}}{\min }\mathbf{L}\left({\mathbf{\theta }}^{sh},{\mathbf{\theta }}^1,\dots ,{\mathbf{\theta }}^T\right)=\underset{\begin{array}{c}{\mathbf{\theta }}^{sh},{\mathbf{\theta }}^1,\dots ,{\mathbf{\theta }}^T\end{array}}{\min }{\left({\hat{\mathcal{L}}}^1\left({\mathbf{\theta }}^{sh},{\mathbf{\theta }}^1\right),\dots ,{\hat{\mathcal{L}}}^T\left({\mathbf{\theta }}^{sh},{\mathbf{\theta }}^T\right)\right)}^{\top }.$$
这个多目标优化目标其实也就是求pareto帕累托最优点。
只有当但所有任务t上${\hat{\mathcal{L}}}^t\left({\mathbf{\theta }}^{sh},{\mathbf{\theta }}^t\right)\le {\hat{\mathcal{L}}}^t\left({\overline{\mathbf{\theta }}}^{sh},{\overline{\mathbf{\theta }}}^t\right)$都成立并且$\mathbf{L}\left({\mathbf{\theta }}^{sh},{\mathbf{\theta }}^1,\dots ,{\mathbf{\theta }}^T\right)\ne \mathbf{L}\left({\overline{\mathbf{\theta }}}^{sh},{\overline{\mathbf{\theta }}}^1,\dots ,{\overline{\mathbf{\theta }}}^T\right)$时，$\theta$优于$\overline{\theta }$。帕累托最优点也就是优于所有其他点的最优解${\theta }^{\star }$。

MGDA（多重梯度下降算法）

作者首先将帕累托静止点定义为满足以下条件的点
（1）存在${\alpha }^1,\dots ,{\alpha }^T\ge 0$，使得${\sum }_{t=1}^T{\alpha }^t=1$ 并且 ${\sum }_{t=1}^T{\alpha }^t{\nabla }_{{\mathbf{\theta }}^{sh}}{\hat{\mathcal{L}}}^t\left({\mathbf{\theta }}^{sh},{\mathbf{\theta }}^t\right)=0$
（2）对所有任务，${\nabla }_{{\mathbf{\theta }}^t}{\hat{\mathcal{L}}}^t\left({\mathbf{\theta }}^{sh},{\mathbf{\theta }}^t\right)=0$。
最优点必定是静止点。因此可以使用如下优化问题来确定a：
min ⁡ α 1 , … , α T { ∥ ∑ t = 1 T α t ∇ θ s h L ^ t ( θ s h , θ t ) ∥ 2 2 ∣ ∑ t = 1 T α t = 1 , α t ≥ 0 ∀ t } \min _{\alpha^1, \ldots, \alpha^T}\left\{\left\|\sum_{t=1}^T \alpha^t \nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)\right\|_2^2 \mid \sum_{t=1}^T \alpha^t=1, \alpha^t \geq 0 \quad \forall t\right\} α1,…,αTmin​⎩ ⎨ ⎧​ ​t=1∑T​αt∇θsh​L^t(θsh,θt) ​22​∣t=1∑T​αt=1,αt≥0∀t⎭ ⎬ ⎫​
该优化问题的解各项${\nabla }_{{\mathbf{\theta }}^t}{\hat{\mathcal{L}}}^t\left({\mathbf{\theta }}^{sh},{\mathbf{\theta }}^t\right)=0$且结果满足KKT条件，要么该解给出一个改进所有任务的下降方向。同时通过最小化这个${\alpha }^t{\nabla }_{{\mathbf{\theta }}^{sh}}{\hat{\mathcal{L}}}^t\left({\mathbf{\theta }}^{sh},{\mathbf{\theta }}^t\right)$的范数，实现如果梯度的范数较大，损失函数下降较快时，对这个损失函数乘以一个小的权重；如果梯度的范数较小，损失函数下降较慢，就乘以一个大的权重。实现让每个损失函数同步进行优化。

优化问题的解

以两个优化为例，优化问题可以被定义为 min ⁡ α ∈ [ 0 , 1 ] ∥ α ∇ θ s h L ^ 1 ( θ s h , θ 1 ) + ( 1 − α ) ∇ θ s h L ^ 2 ( θ s h , θ 2 ) ∥ 2 2 \min _{\alpha \in[0,1]}\left\|\alpha \nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^1\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^1\right)+(1-\alpha) \nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^2\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^2\right)\right\|_2^2 minα∈[0,1]​ ​α∇θsh​L^1(θsh,θ1)+(1−α)∇θsh​L^2(θsh,θ2) ​22​，它的解析解是：
α ^ = [ ( ∇ θ s h L ^ 2 ( θ s h , θ 2 ) − ∇ θ s h L ^ 1 ( θ s h , θ 1 ) ) ⊤ ∇ θ s h L ^ 2 ( θ s h , θ 2 ) ∥ ∇ θ s h L ^ 1 ( θ s h , θ 1 ) − ∇ θ s h L ^ 2 ( θ s h , θ 2 ) ∥ 2 2 ] + , 1 T \hat{\alpha}=\left[\frac{\left(\nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^2\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^2\right)-\nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^1\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^1\right)\right)^{\top} \nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^2\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^2\right)}{\left\|\nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^1\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^1\right)-\nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^2\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^2\right)\right\|_2^2}\right]_{+, \underset{T}{1}} α^= ​ ​∇θsh​L^1(θsh,θ1)−∇θsh​L^2(θsh,θ2) ​22​(∇θsh​L^2(θsh,θ2)−∇θsh​L^1(θsh,θ1))⊤∇θsh​L^2(θsh,θ2)​ ​+,T1​​
其中$[\cdot {]}_{+,\frac{1}{T}}$表示截取到[0,1]。结果可视化如下

在MIL中运用解析解如下：

编解码器架构中的高效优化

上述方法需要计算${\nabla }_{{\mathbf{\theta }}^{sh}}{\hat{\mathcal{L}}}^t\left({\mathbf{\theta }}^{sh},{\mathbf{\theta }}^t\right)$，需要对每个任务的共享参数进行反向传播。因此得到的梯度计算是向前的，然后再T次反向传播，考虑向后传播开销大，这导致了训练时间的线性增加。
作者提出优化目标的上届，这样只需要一次反向传播。作者也进一步证明了在现实假设下，优化这个上界可以得到一个帕累托最优解。
将表示函数和特定于任务的决策函数结合再一起表示为：
$$f^t\left(\mathbf{x};{\mathbf{\theta }}^{sh},{\mathbf{\theta }}^t\right)=\left(f^t\left(\cdot ;{\mathbf{\theta }}^t\right)\circ g\left(\cdot ;{\mathbf{\theta }}^{sh}\right)\right)(\mathbf{x})=f^t\left(g\left(\mathbf{x};{\mathbf{\theta }}^{sh}\right);{\mathbf{\theta }}^t\right)$$
其中g是所有任务共享的表示函数，$f^t$输入表示并用于特定任务的函数。如果表征结果$\mathbf{Z}=\left({\mathbf{z}}_1,\dots ,{\mathbf{z}}_N\right)$，其中${\mathbf{z}}_i=g\left({\mathbf{x}}_i;{\mathbf{\theta }}^{sh}\right)$，由链式求导法则，再根据柯西不等式，可以得到这个上界：
∥ ∑ t = 1 T α t ∇ θ s h L ^ t ( θ s h , θ t ) ∥ 2 2 ≤ ∥ ∂ Z ∂ θ s h ∥ 2 2 ∥ ∑ t = 1 T α t ∇ Z L ^ t ( θ s h , θ t ) ∥ 2 2 \left\|\sum_{t=1}^T \alpha^t \nabla_{\boldsymbol{\theta}^{s h}} \hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)\right\|_2^2 \leq\left\|\frac{\partial \mathbf{Z}}{\partial \boldsymbol{\theta}^{s h}}\right\|_2^2\left\|\sum_{t=1}^T \alpha^t \nabla_{\mathbf{Z}} \hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)\right\|_2^2 ​t=1∑T​αt∇θsh​L^t(θsh,θt) ​22​≤ ​∂θsh∂Z​ ​22​ ​t=1∑T​αt∇Z​L^t(θsh,θt) ​22​
如此优化问题可以被转化为：
min ⁡ α 1 , … , α T { ∥ ∑ t = 1 T α t ∇ Z L ^ t ( θ s h , θ t ) ∥ 2 2 ∣ ∑ t = 1 T α t = 1 , α t ≥ 0 ∀ t } \min _{\alpha^1, \ldots, \alpha^T}\left\{\left\|\sum_{t=1}^T \alpha^t \nabla_{\mathbf{Z}} \hat{\mathcal{L}}^t\left(\boldsymbol{\theta}^{s h}, \boldsymbol{\theta}^t\right)\right\|_2^2 \mid \sum_{t=1}^T \alpha^t=1, \alpha^t \geq 0 \quad \forall t\right\} α1,…,αTmin​⎩ ⎨ ⎧​ ​t=1∑T​αt∇Z​L^t(θsh,θt) ​22​∣t=1∑T​αt=1,αt≥0∀t⎭ ⎬ ⎫​
虽然MGDA-UB是原始优化问题的近似，但作者证明一个定理，表明MGDA-UB在一定假设下产生帕累托最优解。

实验

baseline

（1）uniform scaling：最小化损失函数的统一权重的加权和
（2）single task：独立的处理每个任务
（3）grid search：网格搜索所有的可能权重
（3）Kendall：使用不确定度加权
（4）gradNorm：使用正规化

MultiMNIST

对每个图像都随机选另一个不同的图像，两张图片分别放置左上角和右下角。由此得到两个任务对左上角图片进行分类的任务L和对右下角图片分类的任务R。

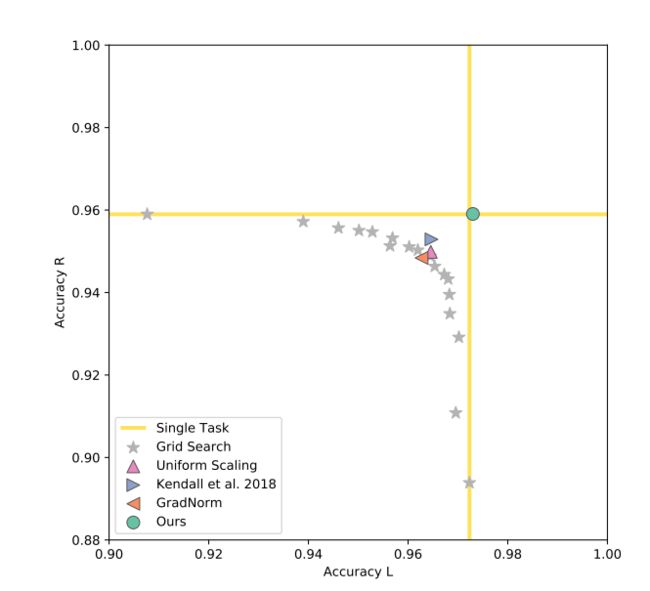
多标签分类

模型需要根据给定的一组attributes确定每个attributes是否适用于输入图像。也就是每一个attributes就一个二分类任务。

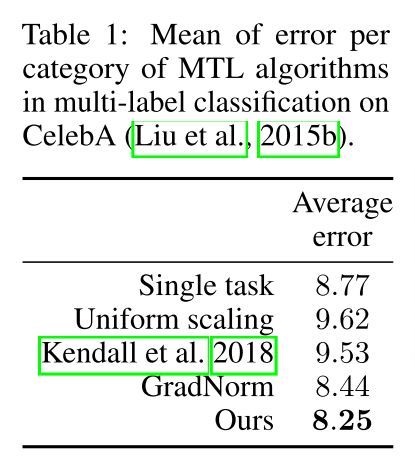
场景理解

给定一个RGB图像，解决三个任务:语义分割，实例分割，monocular深度估计。

论文代码（https://github.com/isl-org/MultiObjectiveOptimization）。