《离散数学》：特殊的图

〇、前言

这一节会重点讨论一下一些特殊的图，这些图会解决一些特殊的问题。

一、欧拉图

给定无向连通图 G，若存在一条路经过 G 中每边一次且仅一次，则该路为欧拉路。若存在一条回路经过 G 中每边一次且仅一次，则该回路称为欧拉回路。

• 具有欧拉路的图称为半欧拉图。
• 具有欧拉回路的图称为欧拉图。

1、（半）欧拉图的判定

这些判定很简单，我们可以找一个欧拉图的充要条件：G的所有结点的度数都是偶数。
同样，我们也可以找一个半欧拉图的充要条件：连通图 G 具有一条连接顶点 u 和 v 的欧拉通路当且仅当 u 和 v 是 G 中仅有的奇数度顶点。

2、有向（半）欧拉图

一个连通有向图具有（单向）欧拉回路的充要条件是图中每个结点的入度等于出度。
一个连通有向图具有单向欧拉路的充要条件是最多除两个结点外的每个结点的入度等于出度，但在这两个结点中，一个结点的入度比出度大1，另一个结点的入度比出度少1。

3、应用欧拉回路的一个经典例子：中国邮递员问题

问题是这样叙述的：邮递员从邮局出发，走遍他负责的街区投递邮件，最后回到邮局。问如何走才能使他走的路最短？
从图论的观点来看，该问题就是：给定一个带权无向图，其中每条边的权为非负实数，求每条边至少经过一次的最短回路。
这个问题是我国管梅谷教授1962年提出的，故被称为中国邮递员问题。

注意：每条边至少走一遍，可以走多遍，只要遍历完后路程最短就是该问题的解。

邮递员负责的街区如下图所示，长度单位是百米，邮局位于 a 处。试设计邮递员的最短投递路线：

解：如果图中有欧拉回路，显然欧拉回路就是最短的投递路线。
图中有 4 个奇数度顶点b, c, e, j，不存在欧拉回路，因此邮递员必须重复走某些边。
为此，只需把 4 个奇数度顶点分成两对，在每对顶点之间沿着某些路重复走一遍，要求重复走的路线最短，以使投递的路线最短。这样就得到了解：

二、哈密尔顿图

和欧拉图类似，人们想要寻找一个能同时遍历图中所有结点，且只遍历一次的回路。如果该回路存在，那么就是一个哈密尔顿图。看起来很简单，其实哈密尔顿图比欧拉图复杂得多，完全不是一个等级。

1859年英国数学家威廉-汉密尔顿图爵士发明了一个小玩具，这个小玩具是一个木刻的正十二面体，每面系正五角形，共有20个顶点，每个顶点标有世界上一个重要城市。他提出一个问题：要求沿正十二面体的边寻找一条路通过20个城市，而每个城市只通过一次，最后返回原地。

事实上，任何一个凸多面体都能“平铺”在平面上，并形成一个“平面图”。

汉密尔顿问题既应用广泛又具有实际价值。

若给无向图的每一条边带上不同的权重，问题又转化为在多条路线中寻找最优路线使得既能实现遍游，又代价最小的最优化问题。

结果不唯一：

严格的定义：给定图G，若有一条路通过 G 中每个顶点恰好一次，则这样的路称为汉密尔顿路； 若有一个圈，通过 G 个每个顶点恰好一次，这样的圈称为汉密尔顿回路（或汉密尔顿圈）。 具有汉密尔顿路的图称为半汉密尔顿图。具有汉密尔顿回路的图称为汉密尔顿图。

1、哈密尔图的判定

但是到目前为止还找不到一个图为汉密尔顿图的充要条件，寻找该充要条件仍是图论中尚未解决的主要问题之一。下面先给出一个简单而有用的必要条件：
定理一：设图G＝〈V ,E〉是汉密尔顿图， 则对于V 的每个非空子集 S， 均有 W(G－S )≤|S| 。

这个定理是在说，对于哈密尔顿图 G，如果删去结点集合 S，那么形成的子图的个数（连通分支）一定少于删去的点集数目。

推论 设图G＝〈V ,E〉是半哈密顿图， 则对于V 的每个非空子集 S，均有 P(G－S )≤|S|+1。

比如：

若取S＝{v1, v4}，则G－S 有3个连通分支故，该图不是哈密顿图。

因为这是一个必要条件，即 P->Q，那么我们是能通过非 Q ->非 P，来证明一个图不是哈密尔顿图，即只能用来证否。因此如果一个图满足 Q，那么它什么都不能证明。

比如彼得森图：任意删除 1 个顶点或者 2 个顶点都连通，任意删除 3 个顶点最多产生两个连通分支。可以进行实验，彼得森图总能满足：W(G－S )≤|S|。

该定理不能证明彼得森图是哈密尔顿图，实际上彼得森图不是哈密尔顿图。

2、哈密尔顿图的充分条件

定理：设 G＝〈V ,E〉是有 n 个结点的简单图，

• (1) 如果任两结点u，v∈V， 均有deg(u)＋deg(v)≥ n－1，则在G中存在一条哈密尔顿路；
• (2) 如果对任两结点u，v∈V， 均有deg(u)＋deg(v)≥ n，则G是哈密尔顿图。

这些是充分条件，即 P->Q，但是非P 什么都推不出来。

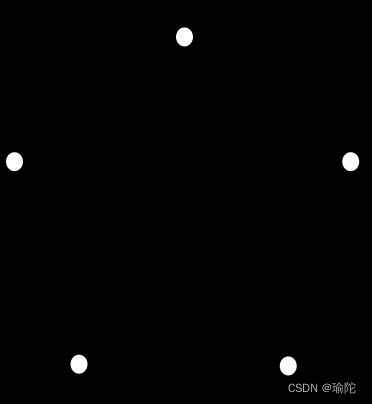
例1： 某地有5个风景点。若每个景点均有两条道路与其他景点相通，问是否可经过每个景点恰好一次而游完这5处？

解 将景点作为结点，道路作为边，则得到一个有5个结点的无向图。
由题意，对每个结点vi，有deg(vi)＝2（i∈N5）。
则对任两点vi，vj（i，j∈N5）均有
deg(vi)＋deg(vj)＝2＋2＝4＝5－1
可知此图一定有一条汉密尔顿路，本题有解。

例 2：考虑在七天内安排七门课程的考试，使得同一位老师所任的两门课程的考试不排在接连的两天中，试证明如果没有老师担任多于四门课程，则符合上述要求的考试安排总是可能的。

如果一个老师担任了四门课，那么显然可以满足要求；但是如果一个老师担任了 5 门课以及以上的课程，那么7 天中至少有两门课相邻，不符合要求。那么怎么用图论来解决呢？

假设 A 老师担任了四门课，每个顶点的度数至少是3，任意两个顶点的度数至少是6，故存在哈密顿路：

假设 A 老师担任了五门课，每个顶点的度数至少是2，任意两个顶点的度数至少是4，4 < 6，故不存在哈密顿路：

例3：货郎担问题

作为汉密尔顿回路的自然推广是著名的货郎担问题。问题是这样叙述的：设有一个货郎，从他所在的城镇出发去n-1个城镇。要求经过每个城镇恰好一次，然后返回原地，问他的旅行路线怎样安排才最经济？从图论的观点来看，该问题就是：在一个带权完全图中找一条权最小的汉密尔顿回路。

解答：

根据上面的充分性定理，完全图一定是一个哈密尔顿图。
因此步骤如下：
(1)由任意选择的结点开始，找与该点最靠近（即权最小）的点， 形成有一条边的初始路径。
(2)设x表示最新加到这条路上的结点，从不在路上的所有结点中选一个与x最靠近的结点， 把连接x与这一结点的边加到这条路上。重复这一步，直到G中所有结点包含在路上。
(3)将连接起始点与最后加入的结点之间的边加到这条路上，就得到一个圈，即为问题的近似解。
遗憾的是，这个方法得到的并不是最小回路，因为贪心法在这个问题中并不能得到最值。

以上就是哈密尔顿图的一些讨论。

三、二分图

二分图的概念很简单，本质上来说，这就是在研究图与图之间的关系。

1、二分图的判定

定理： 一个无向图 G 是二分图，当且仅当 G 中所有回路的长度均为偶数。这是一个充要条件，因此判断起来就很简单。

2、匹配问题

定义： 无向图 G= ，M 为 E 的子集。若 M 中任意两条边都不相邻，则称 M 为 E 中的匹配。若 M 中再添加任意一条边就不是 G 中的匹配了，则称 M 为极大匹配。边数最多的匹配称为最大匹配，最大匹配中边的条数称为 G 的匹配数。其中，M 中的点就是饱和点，若 G 中每个结点都是M饱和点，则称 M 为完美匹配。

鉴于此，有以下结论：

• （1）极大匹配不是任何其它匹配的子集。
• （2）一个图的极大匹配可能是不唯一的。
• （3）一个图的最大匹配可能是不唯一的。
• （4）每个最大匹配都是极大匹配，反之不真。
• （5）在完美匹配中，图 中的每个结点都关联匹配中的一条边。
• （6）如果图 存在完美匹配，则图 的匹配数为图 的阶数的一半，且图 为偶数阶。
• （7）每一个完美匹配都是最大匹配，反之不真。

3、完备匹配

定义：设 $G=<V_1,V_2,E>$ 是一个二分图，|V1| $\le$ |V2|，M为 G 的一个最大匹配，若|M| = |V1|，则M 为G 中V1 到V2 的完备匹配。如果|V2| = |V1|，那么就是完备匹配。

一个充要条件（相异性条件）： $G=<V_1,V_2,E>$ 是一个二分图，|V1| $\le$ |V2|， $G$中存在$V_1$到 $V_2$ 的完备匹配当且仅当 $V_1$ 中任何k个结点至少邻接$V_2$中的k个结点。

一个充分条件：设二分图 $G=<V_1,V_2,E>$ ，如果存在 $t>0$，使得：

• (1) 中每个结点至少关联 条边；
• (2) 中每个结点至多关联 条边。

则$G$中存在$V_1$到$V_2$的完备匹配。

例1：

某学校有3个课外小组：物理组、化学组、生物组。有张、王、李、赵、陈5名同学。问在以下3种情况下能否选出3名不兼任的组长？
已知： 张、王为物理组成员，张、李、赵为化学组成员，李、赵、陈为生物组成员；

解答：

设$V_1，V_2，V_3，V_4，V_5$分别表示张、王、李、赵、陈5名同学。$U_1，U_2，U_3$ 分别表示物理组、化学组、生物组。
这个问题就可以转化为，二分图中 $G<V，U，E>$ 是否存在一个 U到 V 的完备匹配。

答案是显然。

四、平面图

平面图是一种很特殊的图，并且很具有应用的价值，比如设计单层电路板的时候，为了减少感抗、电感等，就使得电器原件之间的走线成为一个平面图。

定义： 设图 $G＝〈V,E〉$是一个无向图，如果能把图 G 的所有结点和边画在平面上，且使得任何两条边除了端点外没有其它的交点，就称图G是一个平面图，否则称图G为非平面图。

以下两个图为最简单的非平面图：$K_3{,}_3$

$K_5$:

前者是变数最少的非平面图，后者是点数最少的非平面图，这两个图也是最基本的非平面图。称为Kuratowski图。

定义：设G是一个平面图，由G的边所包围的区域（其内部不包含图的结点，也不包含图的边）称为G的一个面(Facet)，包围一个面$r$的所有边所组成的回路称面$r$的边界，边界的长度称为该面的次数，记为$deg(r)$。如果面的面积有限，则称该面为有限面，否则称为无限面。如果两个面的边界至少有一条公共边，则称这两个面是相邻的，否则是不相邻的。

定理：一个有限平面图G=〈V，E〉，面的次数之和等于其边数的两倍。

定理（Euler定理)：设图G是连通平面图，有v个结点e条边和r个面，则Euler公式 $v-e+r=2$ 成立。

欧拉公式是凸多面体的公式，为什么能用在这里？

前面说了，任何一个凸多面体都能铺在平面上，并且在平面上形成的是一个平面图，而且，任何一个平面图，只要满足了一些基本条件都一定能映射出一个凸多面体。不满足基本条件的平面图，人们发现它们恰好也是满足欧拉公式的，因此欧拉公式就能用在平面图上了~

关于映射：

对于任何一个平面图（Planar Graph），并不一定能够映射出一个凸多面体（Convex Polyhedron）。

虽然平面图可以在平面上进行绘制，其中顶点由点表示，边由线段表示，并且没有边交叉，但并非所有的平面图都能对应到一个凸多面体。

为了能够映射出一个凸多面体，平面图需要满足一些特定的性质，即必须是一个平面图的特例，称为平面图的平面嵌入（Planar Embedding）。

一个平面嵌入要求满足以下条件：

• 图的边不能交叉。
• 每个面都是一个多边形，包括外部的无限面。
• 每个面的边界由一条简单封闭曲线组成。
• 每个面的边界经过的顶点和边都是连续的，没有间断。

在平面图的平面嵌入满足上述条件的情况下，可以使用多种算法将平面图转换为凸多面体，例如使用凸包算法（Convex Hull Algorithm）或平面图嵌入算法（Planar Embedding Algorithm）。

定理：Euler公式的推广形式：对于任何具有p个连通分支的平面图，有 $v-e+r=p+1$。

定理：设图$G$是有 $v$ 个结点 $e$ 条边的连通简单平面图，若 $v\ge 3$，则 $e\le 3v-6$。

注意：

• 以上只是连通平面图的必要条件，即 $P->Q$，只能用来证否；
• 当结点数和边数较多时，应用Euler公式等判别一个图是非平面图会相当困难。

因此，1930年，Kuratowski给出了判断一个图为平面图的充要条件，这极大地推动了平面图的研究。

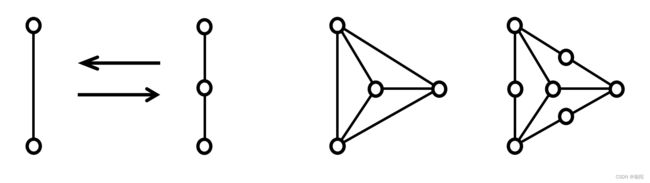
定义：给定两图G1和G2，如果它们是同构的，或者通过反复插入或除去度数为2的结点，使G1和G2同构，则称G1和G2是在2度结点内同构的（或称G1和G2同胚）。

例如以下两组图都是同胚的：

充要条件：一个图是平面图的充要条件是它不包含与$K_3{,}_3$ 或 $K_5$同胚的子图。

一般地，判定图G是否为平面图的步骤如下：

• ①若$e<9或v<5$，则G是平面图；如果$e>3v-6$，则G是非平面图；
• ②如果 G 是不连通的，则分别检测每个分图；当且仅当每个分图都是平面图时，G是平面图；
• ③如果G中存在割点，可把图G的割点删除，构成若干个不含割点的连通子图。显然，G是平面图当且仅当每个连通子图是平面图；
• ④移去自回路；
• ⑤否则利用Kuratowski定理检测，或尝试看能否画一个相应的边不相交的图解；
• ⑥移去平行边。
• 反复运用⑤ 和⑥，并结合①进行检测。

以上就是关于几种常见特殊的图的讨论，全文完，感谢阅读。