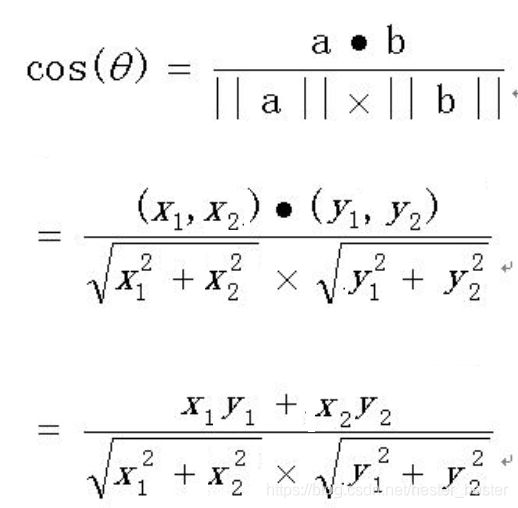深度学习-Word Embedding的详细理解（包含one-hot编码和cos余弦相似度）

        这两天在费劲的研究单词嵌入Embedding，好不容易稍微懂了一点，赶紧记下来省的忘了。

ont-hot编码：

        一般在输入的时候，都会将所有的单词看作一个向量，只把当前的单词置为1，以下为几组单词表和单词向量的表示方式：

当前单词为apple

[apple,man,banana,cat......,orange,kite]

[1,0,0,0...0,0]

当前单词为cat

[apple,man,banana,cat......,orange,kite]

[0,0,0,1...0,0]

 

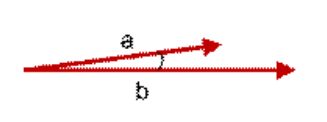
cos余弦相似度：

图中向量a和向量b夹角重合，余弦值等于1，表示完全相同

图中向量a和向量b夹角很小，余弦值接近1，表示很相似

图中向量a和向量b夹角很大，余弦为负，表示相似度很低

 

二维坐标系中的向量相似度计算：

因此，当向量不是二维而是n维时，可以得出以下公式：

举例，对以下两句话判断相似度：

        这只小狗特别可爱，那只小猫也很可爱。

        这只小狗不可爱，那只小猫可爱。

划分词语：

        这只/小狗/特别/可爱，那只/小猫/也/很/可爱。

        这只/小狗/不/可爱，那只/小猫/可爱。

生成词汇向量：

        【这只，小狗，特别，可爱，那只，小猫，也，很，不】

两句话对应的向量，元素即对应单词在该句中出现的频率：

        [1,1,1,2,1,1,1,1,0]

        [1,1,0,2,1,1,0,0,1]

带入公式计算：

 

        因此对于上边那个one-hot编码，每一个单词对应的向量只有一位为1其余为0，值是离散的，所以各向量之间的cos余弦相似度为0，这样很不利于判断句子中各单词的关系因此要进行降维，将离散值变为连续值，使不同向量的相似度发生改变而不全部为0.

 

词嵌入Word Embedding:

        通常一个词在一开始的one-hot编码时维度为几千上万的，这时候，向量之间cos余弦相似度为0，完全没有联系，通常较为完整的代码中进行降维会通过Embedding使之降维到128维或者256维，降维后每个元素表示的是一个概率值，是连续的。

举例，假设有十个名词：足球、比赛、教练、队伍、裤子、上衣、编织、折叠、拉，这里降到二维可视化显示如图所示：

         我们可以发现，十个词基本被分为了三类，每一类包含的内容大致很像，有都属于衣物的，有都属于动作的，有都属于运动的。

 

对于将一个高维one-hot编码向量降维成为一个低维向量，简单代码如下：

import torch as t
from torch import nn as nn

embedding = nn.Embedding(10, 4)  # num_embeddings表示10个词，embedding_dim表示每个词2维
input = t.arange(0, 6).view(3, 2).long()  # 将0-6中6个数字分配为3个句子，每个句子有2个词（其实是3行2列的矩阵），其中N为3，M为2
output = embedding(input)#如果Embedding层的输入形状为NxM（N是batch size,M是序列的长度），则输出的形状是N*M*embedding_dimension.
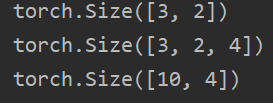
print(input.size())
print(output.size())
print(embedding.weight.size())   #权重大小为num_embeddings*embedding_dim

运行结果：

单独的看嵌入的那个过程是这个样的：这里注意画成矩形只是为了方便看，这都是矩阵，是高维的，不要理解成平面矩形的二维。

对于整个嵌入层来说，执行过程如下图，上图的10->4可以认为是对高这个维度进行变化：

 注意Embedding的输入形状是n*w，n是batch_size表示一共有几个句子，就是图中的3，w是seq_size表示每个句子有几个单词，就是图中的2，embedding_dim表示降维后的维度，就是图中的4，因此Embedding的最终输出维n*w*embedding_dim。