华为又开始放大招了?CV新架构:VanillaNet: the Power of Minimalism in Deep Learning 论文阅读笔记
华为又开始放大招了?CV新架构:VanillaNet: the Power of Minimalism in Deep Learning 论文阅读笔记
- 一、Abstract
- 二、引言
- 三、单个 Vanilla 的神经结构
- 四、训练 VanillaNet
-
- 4.1 深度训练策略
- 4.2 Series Informed Activation Function
- 五、实验
-
- 5.1 消融实验
-
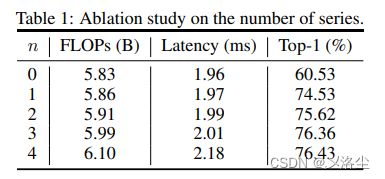
- 激活函数中 series 数量的影响
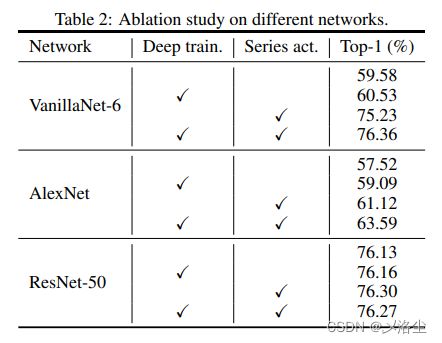
- 训练技巧的影响
- 捷径分支的影响
- 5.2 注意力的可视化
- 5.3 与 SOTA 架构的比较
- 5.4 COCO 数据集上的实验
- 六、结论
- 附录 A:网络结构
- 附录 B:训练细节
写在前面
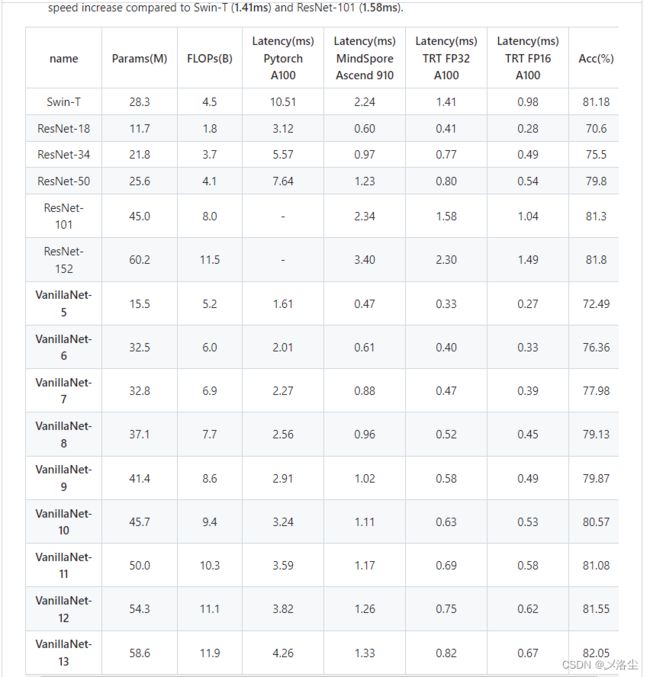
前两天在 VALSE 会议上,华为这篇文章吓我一跳,说实话这性能有点炸裂。看了下 Github 上面的表格,这个参数量随着层数的递增也是恐怖,但是推理速度真是远超前面的模型太多。
- 论文地址:VanillaNet: the Power of Minimalism in Deep Learning
- 代码地址:https://github.com/huawei-noah/VanillaNet
- 预训练模型地址:https://gitee.com/mindspore/models/tree/master/research/cv/vanillanet
- 预计投稿:24 年的某个顶会
- 其他微信文章解读:华为诺亚极简网络,靠13层就拿下83%精度(附源代码)
- Ps:23 年每周一篇博文阅读笔记,主页更多干货,欢迎关注吖,期待 5 千粉丝有您的参与呦~
一、Abstract
纵观整个 Abstract,没啥具体内容,就是说本文提出的 VanillaNet 能够一手左勾拳 ResNet,右勾手 Swim-Transformer 等。主要原因在于避免了超深、捷径、自注意力机制的引入,也没有复杂的激活函数。
二、引言
第一段浅谈 AI 的发展与作用,第二段从 AlexNet 的引入,ResNet 的后续,表明这模型啊,是越来越设计的复杂了,但同时性能也越来越好。第三段是 Transformer 的主场,仍然强调模型的深度。第四段是承上启下的转折,表明更深和更复杂的模型结构很难去部署了。第五段表明问题,扁平的网络会出现梯度消失问题,而一些深度网络的性能远超之前的 AlexNet、VGG,因而再有很少人关注模型结构的设计了。
第六段引出话题,本文提出 VanillaNet,模型结构简单:去掉了模型的超深度、捷径分支、自注意力操作。相应地提出了一种训练策略,逐渐地消除非线性层,来保持推理速度。为了增强网络的非线性,提出基于 series 的激活函数,效果远超其他模型。最后来一句,VanillaNet 都这么强了,赶紧来 follow 我的工作吧。
三、单个 Vanilla 的神经结构
大部分 SOTA 的分类模型由三个部分组成:stem 块将输入的 3 通道图像变为多通道,并伴随下采样,主要的 body 模块用于学习有用的信息,一个全连接层用于分类器的输出。body 模块有四个阶段,每个阶段由多个相同的 blocks 堆叠而成。每个阶段之后特征通道数量将会增加,而宽度和高度将会减小。
下一段吐槽下 ResNet 和 ViT 整的太多太深了,而且 ViT 需要多个自注意力层。
目前 AI 芯片的发展,当初制约的 FLOPs 或者参数量目前已不再是瓶颈了,因为老黄的 NVIDIA GPU 确实发展起来了。于是模型的复杂设计和更深的 blocks 成了制约速度的主要因素。于是本文提出 VanillaNet,如下图所示:

VanillaNet 仍然是三个阶段的设计,不同的是深度,每个阶段仅用一层来搭建。
以 6 层的 VanillaNet 举个例子,stem:卷积层 4 × 4 × 3 × C 4\times4\times3\times C 4×4×3×C,步长为 4 4 4,将 3 3 3 层通道的输入图像映射到 C C C 个通道上。在阶段 1,2,3 上,使用步长为 2 2 2 的最大池化层来减小特征图的尺寸,而通道数量增加 2 2 2 倍。在阶段 4,由于之后的平均池化而不增加通道数量。最后一层全连接层输出分类结果。每个卷积层的 kernel 尺寸都为 1 × 1 1\times1 1×1,之后跟着一层激活层,同时也加了一层 Batch 归一化。这就是全部的结构了,没有捷径和额外的 blocks。
由于 VanillaNet 相对简单且是个浅层网络,这弱化了模型的性能,于是提出一系列技术来增强其非线性。
四、训练 VanillaNet
4.1 深度训练策略
训练两个卷积层加个激活层的策略不同于训练单个卷积层,需要随着训练 epoch 的增加,逐渐地减少激活函数。在训练结束时,两个卷积层就能融合成一个从而减少推理时间。
对于一个激活函数 A ( x ) A(x) A(x),例如 ReLU 和 Tanh,用一种独特的映射来组合:
A ′ ( x ) = ( 1 − λ ) A ( x ) + λ x A'(x)=(1-\lambda)A(x)+\lambda x A′(x)=(1−λ)A(x)+λx
其中 λ \lambda λ 为平衡修改后的 A ′ ( x ) A'(x) A′(x) 激活函数的非线性超参数。令 e e e、 E E E 分别表示当前的 epoch 和总体的 epoch 数量,则 λ = e E \lambda=\frac{e}{E} λ=Ee。于是在训练开始时, e = 0 , A ′ ( x ) = A ( x ) e=0,A'(x)=A(x) e=0,A′(x)=A(x),意味着模型有很强的非线性。随着训练收敛,最终有 A ′ ( x ) = x A'(x)=x A′(x)=x,表明两个卷积层间没有激活函数了。
接下来将每层 batch 归一化和后续的卷积变成单个卷积操作。
令 W ∈ R C o u t × ( C i n × k × k ) W\in\mathbb R^{C_{out}\times(C_{in}\times k\times k)} W∈RCout×(Cin×k×k), B ∈ R C o u t B\in \mathbb R^{C_{out}} B∈RCout 分别为卷积层的权重和偏置,输入 C i n C_{in} Cin 个通道,输出 C o u t C_{out} Cout 个通道,卷积核尺寸为 k k k。batch 归一化的尺度、平移、平均、微分分别用 γ , β , μ , σ ∈ R C o u t \gamma,\beta,\mu,\sigma\in\mathbb{R}^{C_{out}} γ,β,μ,σ∈RCout 表示,于是 batch 归一化和卷积的融合操作可表示为:
W i ′ = γ i σ i W i , B i ′ = ( B i − μ i ) γ i σ i + β i W_i'=\frac{\gamma_i}{\sigma_i}W_i,B_i'=\frac{(B_i-\mu_i)\gamma_i}{\sigma_i}+\beta_i Wi′=σiγiWi,Bi′=σi(Bi−μi)γi+βi其中下标 i ∈ { 1 , 2 , … , C o u t } i\in\{1,2,\ldots,C_{out}\} i∈{1,2,…,Cout} 表示第 i i i 个通道的输出值。
之后融合两个 1 × 1 1\times1 1×1 卷积。输入和输出特征分别表示为 x ∈ R C i n × H × W x\in\mathbb R^{C_{in}\times H\times W} x∈RCin×H×W、 y ∈ R C o u t × H ′ × W ′ y\in\mathbb R^{C_{out}\times H'\times W'} y∈RCout×H′×W′,于是卷积操作可表示为:
y = W ∗ x = W ⋅ i m 2 c o l ( x ) = W ⋅ X y=W*x=W\cdot\mathrm{im}2\mathrm{col}(x)=W\cdot X y=W∗x=W⋅im2col(x)=W⋅X其中 ∗ * ∗ 表示卷积操作, ⋅ \cdot ⋅ 表示矩阵乘法, X ∈ R ( C i n × 1 × 1 ) ( H ′ × W ′ ) X\in\mathbb R^{(C_{in}\times1\times1)(H'\times W')} X∈R(Cin×1×1)(H′×W′) 源于 im2col {\text{im2col}} im2col 操作,将输入转化为对应于卷积核的形状。对于 1 × 1 1\times1 1×1 卷积来说,无需在重叠的部分上滑动卷积核(因为没有重叠部分)。于是将两个卷积层的权重矩阵表示为 W 1 W^1 W1 和 W 2 W^2 W2,没有激活函数的两个卷积操作可表示为:
y = W 1 ∗ ( W 2 ∗ x ) = W 1 ⋅ W 2 ⋅ im 2 col ( x ) = ( W 1 ⋅ W 2 ) ∗ X y=W^1*(W^2*x)=W^1\cdot W^2\cdot\text{im}2\text{col}(x)=(W^1\cdot W^2)*X y=W1∗(W2∗x)=W1⋅W2⋅im2col(x)=(W1⋅W2)∗X至此,两个 1 × 1 1\times1 1×1 卷积顺利融合且并未降低推理速度。
4.2 Series Informed Activation Function
目前一些主流的激活函数有 Rectified Linear Unit (ReLU) 及其变体 PReLU、GeLU、Swish,受限于简单和浅层网络的非线性,相较于深层网络,这些激活函数还没有被系统研究过。
有两种方式来提升神经网络的非线性:堆叠非线性激活层或增加每层激活层的非线性,大多数的主流网络选择前者,这就使得在并行计算时会留有很高的潜力。
其中一个直接的想法是去提高堆叠激活层的非线性能力,而一连串地堆叠激活层是深度网络的关键,相比之下,转向同时堆叠激活层是个不错的办法。将单层激活函数表示为 A ( x ) A(x) A(x),其中 x x x 为输入,该函数可以是 ReLU 和 Tanh。堆叠 A ( x ) A(x) A(x) 可以表示为:
A s ( x ) = ∑ i = 1 n a i A ( x + b i ) A_s(x)=\sum_{i=1}^n a_i A(x+b_i) As(x)=i=1∑naiA(x+bi)其中 n n n 表示堆叠激活函数的数量, a i a_i ai、 b i b_i bi 分别是激活函数的尺度和偏置。激活函数的非线性可通过同时堆叠而增强。
为了进一步增强 Series 的近似能力,通过改变输入的邻居来改变输入,从而学习全局信息,类似于 BNET。具体来说,给定输入特征 X ∈ R H × W × C X\in\mathbb R^{H\times W\times C} X∈RH×W×C,其中 H H H、 W W W、 C C C 分别是输入的宽、高、通道数量。于是激活函数塑造如下:
A s ( x h , w , c ) = ∑ i , j ∈ { − n , n } a i , j , c A ( x i + h , j + w , c + b c ) A_s(x_{h,w,c})=\sum\limits_{i,j\in\{-n,n\}}a_{i,j,c}A(x_{i+h,j+w,c}+b_c) As(xh,w,c)=i,j∈{−n,n}∑ai,j,cA(xi+h,j+w,c+bc)其中 h ∈ { 1 , 2 , … , H } h\in\{1,2,\ldots,H\} h∈{1,2,…,H}、 w ∈ { 1 , 2 , … , W } w\in\{1,2,\ldots,W\} w∈{1,2,…,W}、 c ∈ { 1 , 2 , … , C } c\in\{1,2,\ldots,C\} c∈{1,2,…,C}。当 n = 0 n=0 n=0 时, A s ( x ) = A ( x ) A_s(x)=A(x) As(x)=A(x)。本文采用 ReLU 作为激活函数来构建 series。
接下来分析其计算复杂度:对于一个有着卷积核尺寸为 K K K 的卷积层,输入和输出通道数量分别为 C i n C_{in} Cin、 C o u t C_{out} Cout,计算复杂度为:
O ( C O N V ) = H × W × C i n × C o u t × k 2 \mathcal{O}(\mathrm{CONV})=H\times W\times C_{in}\times C_{out}\times k^2 O(CONV)=H×W×Cin×Cout×k2而 series 激活层的成本为:
O ( SA ) = H × W × C i n × n 2 \mathcal{O}(\text{SA})=H\times W\times C_{in}\times n^2 O(SA)=H×W×Cin×n2于是:
O ( CONW ) O ( SA ) = H × W × C i n × C o u t × K 2 H × W × C i n × n 2 = C o u t × k 2 n 2 \frac{\mathcal{O}(\text{CONW})}{\mathcal{O}(\text{SA})}=\frac{H\times W\times C_{in}\times C_{out}\times K^2}{H\times W\times C_{in}\times n^2}=\frac{C_{out}\times k^2}{n^2} O(SA)O(CONW)=H×W×Cin×n2H×W×Cin×Cout×K2=n2Cout×k2以 VanillaNet-B 中第 4 4 4 个阶段为例,其中 C o u t = 2048 C_{out}=2048 Cout=2048, k = 1 k=1 k=1, n = 7 n=7 n=7,上式比例为 84 84 84。因此提出的激活层计算复杂度比卷积层低。
五、实验
ImageNet 数据集。
5.1 消融实验
激活函数中 series 数量的影响
训练技巧的影响
捷径分支的影响
5.2 注意力的可视化
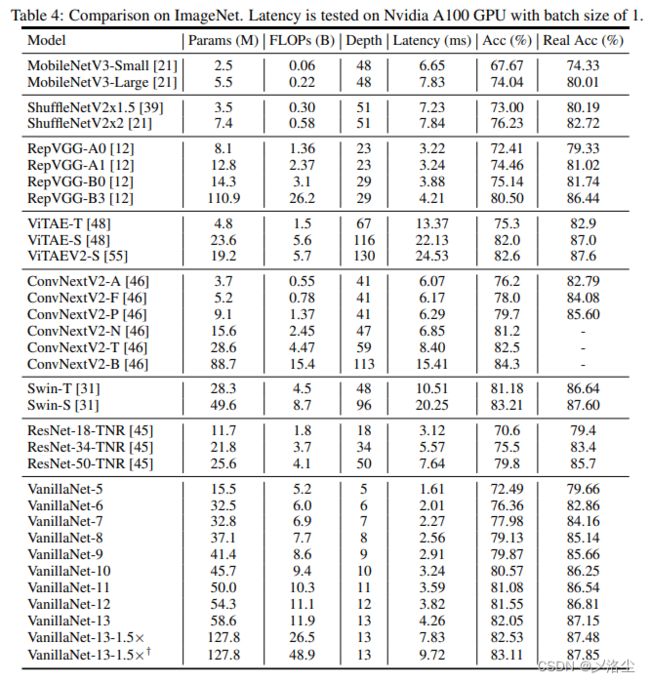
5.3 与 SOTA 架构的比较
5.4 COCO 数据集上的实验
六、结论
本文研究了简单、浅层神经网络的可行性,为训练 VanillaNets 提出一种深度训练策略与 series 激活函数来增强模型的非线性。实验结果表明 VanillaNets 很有效,希望大家都来试一下。
附录 A:网络结构
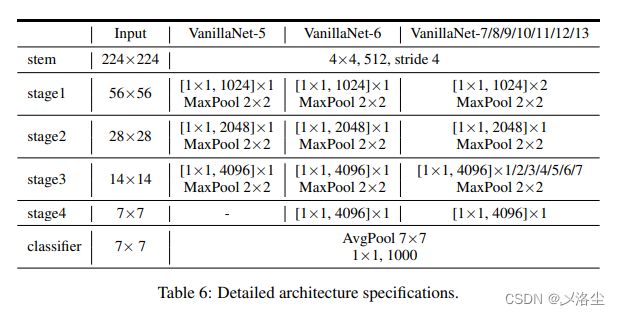
其中每个卷积层后接一个激活层。对于 VanillaNet-13-1.5×,通道数量 x1.5。对于 VanillaNet-13-1.5׆,进一步在阶段 2,3,4 采用自适应池化,相应的形状为 40 × 40 40\times40 40×40、 20 × 20 20\times20 20×20、 10 × 10 10\times10 10×10。
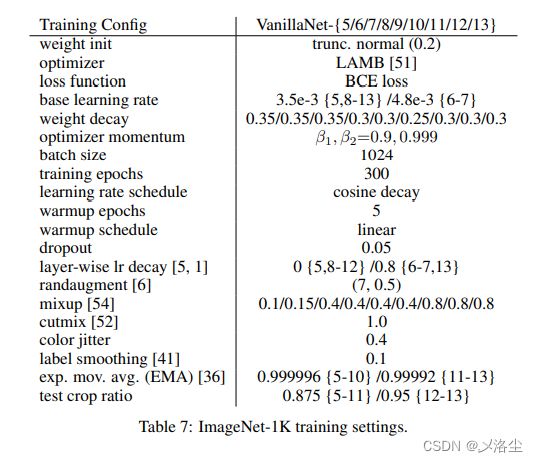
附录 B:训练细节
华为的这篇文章短小精悍,着实体现了功底。在这个“深度”学习时代,敢于挑战下浅层网络,实属牛批。