【论文精读】LORA: LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS
LORA: LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS
- 前言
- ABSTRACT
- 1. INTRODUCTION
- 2. PROBLEM STATEMENT
- 3. AREN'T EXISTING SOLUTIONS GOOD ENOUGH?
-
- Adapter Layers Introduce Inference Latency
- Directly Optimizing the Prompt is Hard
- 4. OUR METHOD
-
- 4.1 LOW-RANK-PARAMETRIZED UPDATE MATRICES
-
- A Generalization of Full Fine-tuning
- No Additional Inference Latency
- 4.2 APPLYING LORA TO TRANSFORMER
-
- Practical Benefits and Limitations
- 5. EMPIRICAL EXPERIMENTS
-
- 5.1 BASELINES
- 5.2 ROBERTA BASE/LARGE
- 5.3 DEBERTA XXL
- 5.4 GPT-2 MEDIUM/LARGE
- 5.5 SCALING UP TO GPT-3 175B
- 6. RELATED WORKS
-
- Transformer Language Models
- Prompt Engineering and Fine-Tuning
- Parameter-Efficient Adaptation
- Low-Rank Structures in Deep Learning
- 7. UNDERSTANDING THE LOW-RANK UPDATES
-
- 7.1 WHICH WEIGHT MATRICES IN TRANSFORMER SHOULD WE APPLY LORA TO?
- 7.2 WHAT IS THE OPTIMAL RANK r FOR LORA?
-
- Subspace similarity between different r
- Subspace similarity between different random seeds
- 7.3 HOW DOES THE ADAPTATION MATRIX ∆W COMPARE TO W ?
- 8. CONCLUSION AND FUTURE WORK
- 阅读总结
前言
当下大模型时代最火的低资源微调大模型方法之一,方法简单易懂,道理清晰明了,对未来的工作有很强的启发性。如果想要深入了解LoRA的底层原理,建议仔细看一看这篇文章,如果只是应用,那么简单了解就好了~
ABSTRACT
大模型预训练后的全量微调往往由于算力缺口而不可行,因此本文提出低秩适应,即LoRA,它冻结了预训练模型的权重,并将可训练的低秩分解矩阵注入到Transformer的每一层,大大减少了下游任务的参数量。与GPT-3相比,LoRA可以减少10000倍的参数训练量和3倍的显存需求。LoRA在RoBERTa、DeBERTa、GPT-2、GPT-3上表现与微调相当或更好,并且与Adapters相比没有额外的推理延迟。LoRA与部分模型的集成实现见https://github.com/microsoft/LoRA。
1. INTRODUCTION
传统的微调范式需要更新所有模型参数,但是随着模型的规模越来越大,带来了极大的不便和挑战。很多想法希望只微调一部分参数或者为新任务添加额外的模块,这样可以大大提高部署时的效率,但是这些方法通过扩展模型深度或减少模型的可用序列长度来引入推理延迟,并且与微调结果有差距。
作者发现学习到的过度参数化模型(模型规模远超任务所需)实际上存在于较低的内在维度上,即参数的权重集中在具有较高信息量的维度上,忽略了其它维度,这导致了模型在一个较低的内在维度空间中进行有效的表示和学习。因此作者假设模型在adaptation的过程中也有”内在秩“,从而提出了低秩适应方法——LoRA。LoRA通过优化自适应过程中密集层变化的秩分解矩阵来间接训练神经网络中的密集层,同时保持预训练的权重不变(Frozen)。如下图所示:

以GPT-3为例,上图的r甚至为1或2(完整rank为12288)就足够了,这表明LoRA既能节省空间,又能减少计算成本。
总结一下,LoRA的优势如下:
- 预训练模型可以共享为不同任务构建的LoRA模块。
- LoRA让训练更高效,降低了硬件门槛达3倍多。
- 简单的线性设计允许在部署时可以将训练矩阵和冻结矩阵合并,不会引入推理延迟。
- LoRA可以结合多种方法,例如prefix-tuning。
2. PROBLEM STATEMENT
LoRA方法是通用的范式,本文以自然语言任务为例,来证明其优越性。
如果是full fine-tuning,需要对每个参数进行学习,在存储和部署上都极具挑战。目标函数如下所示:
max Φ ∑ ( x , y ) ∈ Z ∑ t = 1 ∣ y ∣ log ( P Φ ( y t ∣ x , y < t ) ) \max _{\Phi} \sum_{(x, y) \in \mathcal{Z}} \sum_{t=1}^{|y|} \log \left(P_{\Phi}\left(y_t \mid x, y_{
而LoRA相当于修改了目标函数,只对参数量极少的 Θ \Theta Θ进行优化,如下所示:
max Θ ∑ ( x , y ) ∈ Z ∑ t = 1 ∣ y ∣ log ( p Φ 0 + Δ Φ ( Θ ) ( y t ∣ x , y < t ) ) \max _{\Theta} \sum_{(x, y) \in \mathcal{Z}} \sum_{t=1}^{|y|} \log \left(p_{\Phi_0+\Delta \Phi(\Theta)}\left(y_t \mid x, y_{
3. AREN’T EXISTING SOLUTIONS GOOD ENOUGH?
自动迁移训练以来,许多工作都在寻求让模型在参数和计算上高效性的方法,第六节会有所提及。以语言模型为例,在高效适应方面有两种突出的策略:添加adapter层或者优化输入层的Prompt。但是这两种方式都有局限性,特别是在大规模和低延迟场景。
Adapter Layers Introduce Inference Latency
适配器的形式有多种,虽然可以通过剪枝或者多任务设置来减少整体延迟,但是适配器中的额外计算无法消除。虽然Adapter中的参数量很小,但是大型神经网络只能顺序处理Adapter,无法发挥其并行计算的优势来保持低延迟,在在线推理场景,往往只有一个样本,这使得Adapter的延迟更加明显。此外,如果对模型进行切分训练,额外的深度需要更多的同步GPU操作,例如AllReduce和Broadcast。

Directly Optimizing the Prompt is Hard
Prefix tuning难以优化,性能不稳定。此外,微调保留一部分序列或导致下游任务输出长度的减少,这可能会对prompt的微调产生不利的影响。
4. OUR METHOD
4.1 LOW-RANK-PARAMETRIZED UPDATE MATRICES
神经网络中包含很多执行矩阵乘法的密基层,权重都是满秩的,作者受“内在秩”的启发,对预训练的权重矩阵 W 0 W_0 W0,通过低秩分解 W 0 + Δ W = W 0 + B A W_0 + \Delta W = W_0 + BA W0+ΔW=W0+BA来约束其更新,其中 B ∈ R d × r B \in \mathbb{R}^{d \times r} B∈Rd×r, A ∈ R r × k A \in \mathbb{R}^{r \times k} A∈Rr×k。训练过程中, W 0 W_0 W0被冻结,A和B进行参数的更新。对于 h = W 0 x h = W_0x h=W0x,我们修改后的前向传播如下:
h = W 0 x + Δ W x = W 0 x + B A x h = W_0x + \Delta Wx = W_0x + BAx h=W0x+ΔWx=W0x+BAx
作者对A使用随机高斯分布初始化,对B使用0初始化,因此 Δ W \Delta W ΔW在开始训练时为0,然后使用 α r \frac{\alpha}{r} rα对 W x Wx Wx进行缩放。 α \alpha α在微调时可以像学习率一样调整,这种scaling的方式可以在改变r时不需要重新去调节超参数。
A Generalization of Full Fine-tuning
一种更通用的微调范式是只微调预训练参数的子集。LoRA进一步降低了约束,在训练中不要求满秩,可以更灵活应对新任务。总而言之,随着模型可训练参数的增加,LoRA大致收敛到原始模型,而基于Adapter的方法收敛到MLP,基于Prefix Tuning的方法收敛到不能接受长输入的模型。
:::info
这样一对比,随着可训练参数量的增加,LoRA的优势就更加显现出来,我最差也不过和原始模型一样的开销,而另外两种方法不是开销更大了就是可用性大大降低了。
:::
No Additional Inference Latency
推理过程和原先一致,当更换不同的下游任务时,只需要更换不同的BA来恢复 W 0 W_0 W0,大大减少了内存开销,并且保证了推理过程不会引入任何额外的延迟。
4.2 APPLYING LORA TO TRANSFORMER
原则上,LoRA可以用于任何神经网络的子集中,以减少可训练参数。Transformer架构中,自注意力模块有四个权重矩阵( W q , W k , W v , W o W_q,W_k,W_v,W_o Wq,Wk,Wv,Wo),MLP模块有两个。可以将 W q W_q Wq(或者 W k , W v W_k, W_v Wk,Wv)视为 d m o d e l × d m o d e l d_{model} \times d_{model} dmodel×dmodel的单个矩阵,作者只对下游任务注意力的权重进行调整,并冻结MLP模块,以实现简单性和高效性。
Practical Benefits and Limitations
LoRA最显著的优势在于极大节省显存空间,避免了GPU的I/O瓶颈。另外,可以通过仅交换 LoRA 权重而不是所有参数来以更低的成本在任务之间切换。但是LoRA也有自己的局限性,在批处理不同任务的数据时,需要对每个任务进行单独处理,实现复杂,但是也可以实现根据任务动态选择LoRA模块。
5. EMPIRICAL EXPERIMENTS
5.1 BASELINES
作者将LoRA和以下方法进行了实验上的对比:
- 微调。
- Bias-only or BitFit。只训练bias向量,同时冻结其它参数。
- Prefix-embedding tuning (PreEmbed)。在输入token中插入特殊的token。是线性的Embedding,通常无法对应到词表。可训练的参数数量是 ∣ Θ ∣ = d m o d e l × ( l p + l i ) |\Theta|=d_{model} \times (l_p + l_i) ∣Θ∣=dmodel×(lp+li)。
- Prefix-layer tuning (PreLayer)。学习每一层Transformer的激活输出,可训练的参数量是 ∣ Θ ∣ = L × d m o d e l × ( l p + l i ) |\Theta|=L \times d_{model} \times (l_p + l_i) ∣Θ∣=L×dmodel×(lp+li),L是Transformer的层数。
- Adapter tuning。在自注意力模块(和 MLP 模块)和后续的残差连接之间插入适配器层。Adapter是两层带有偏差的全连接层,当然还有很多变种。
5.2 ROBERTA BASE/LARGE
RoBERTa优化了BERT的预训练方法,在不引入更多参数的情况下提升其性能。为了对比不同方法的性能,使用GLUE基准进行评估。所有任务采用相同的batch_size,并且不是在通用模型下测试,而是在不同任务的预训练模型下测试,来验证其在不同任务上的能力。
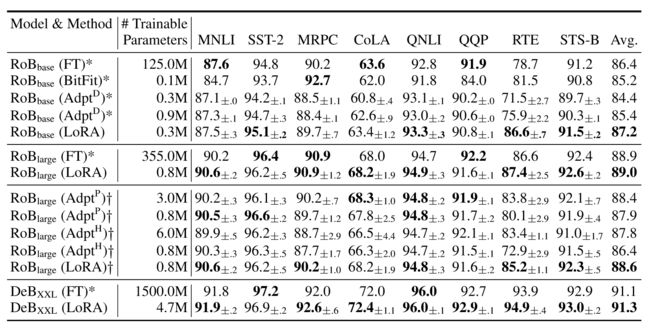
5.3 DEBERTA XXL
DeBERTa是另一个BERT的变体,经过了更大规模的训练,结果如上表的下面所示。
5.4 GPT-2 MEDIUM/LARGE
LoRA在NLU模型上基于可以替代完全微调,因此希望在NLG模型上也能够有很好的表现,以GPT-2为例,下面是E2E NLG挑战赛上的结果:

5.5 SCALING UP TO GPT-3 175B
进一步扩大模型的规模,应用在175B的GPT-3上,结果如下表所示:

注意到并不是所有模型的可训练参数越大越好。如下图所示,观察到当使用超过256个特殊token进行前缀嵌入调整或使用超过32个特殊token进行前缀层tuning时,性能显著下降。

6. RELATED WORKS
Transformer Language Models
略。
Prompt Engineering and Fine-Tuning
GPT-3的输出结果很大程度上决定于其输入提示,需要一种经验主义的技巧来编写格式化提示,最大化提高模型在所需任务上的性能,称为Prompt工程。
微调是将预训练模型重新训练去解决特定的任务。完全微调由于占据巨大内存空间,因此门槛很高。
Parameter-Efficient Adaptation
为了参数有效性学习,很多工作设计了Adapter层嵌入在神经网络中,本文的低秩分解也有异曲同工之妙,LoRA的优势在于学习的权重在推理过程中与固定的权重合并,因此不会引入延迟。此外,prefix-tuning的出现虽然可以代替微调,但是会占用输入可用token长度。
Low-Rank Structures in Deep Learning
低秩结构在机器学习中很普遍,在过度参数化的神经网络模型中就更为常见了,很多方法考虑了低秩分解,但是没有想到冻结其它参数。还有理论认为,低秩适应可能对对抗学习有用。
7. UNDERSTANDING THE LOW-RANK UPDATES
本节通过一系列实证研究来回答以下问题:
- 给定参数预算约束,应该调整Transformer中权重矩阵的哪个子集以最大化下游性能?
- 最优的适应矩阵 Δ W \Delta W ΔW真的是低秩矩阵吗,在实践中秩应该多少更合适?
- Δ W \Delta W ΔW和 W W W之间有什么联系?二者是否高度相关, Δ W \Delta W ΔW有多大?
问题2,3其实揭示了微调的真正原则。
7.1 WHICH WEIGHT MATRICES IN TRANSFORMER SHOULD WE APPLY LORA TO?
只考虑自注意模块中权重矩阵,结果如下:
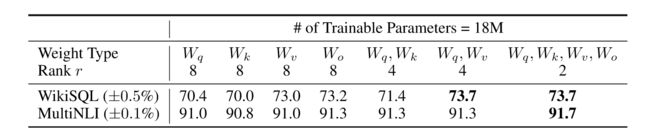
注意到将同时调整 Δ W q \Delta W_q ΔWq或 Δ W k \Delta W_k ΔWk会导致性能降低,而同时调整 Δ W q \Delta W_q ΔWq和 Δ W v \Delta W_v ΔWv会产生最佳结果。因此,调整更多权重矩阵的参数比仅调整某一个权重矩阵的参数更可取。
7.2 WHAT IS THE OPTIMAL RANK r FOR LORA?
根据选取不同的r进行实验,结果如下表所示:
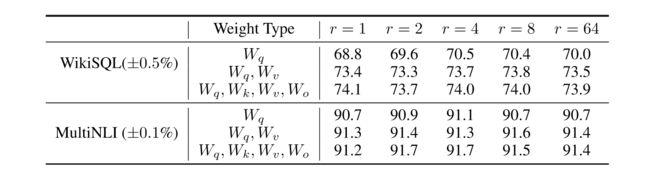
LoRA在非常小的r下表现出竞争力,这更说明更新矩阵 Δ W \Delta W ΔW具有非常小的内在秩,为了进一步支持这种发现,作者在不同的随机种子设定下进行实验,都取得了相似的结果。
但是这里并不能说明对于所有的任务,非常小的内在秩都有很好的表现,这是和具体的下游任务相关的,如果下游任务和预训练任务差距过大,那么微调相当于重新训练,这种情况下高秩往往比低秩要好。
Subspace similarity between different r
给定秩为8和64的用预训练模型学习到适应矩阵,进行奇异值分解, 并获得对应秩的右奇异矩阵,当前的问题是,对于前i个奇异向量张成的子空间(1 ≤ i ≤ 8),有多少包含在秩为64的矩阵所张成的子空间中。作者使用基于格拉斯曼距离的归一化子空间来衡量。
ϕ ( A r = 8 , A r = 64 , i , j ) = ∥ U A r = 8 i ⊤ U A r = 64 j ∥ F 2 min ( i , j ) ∈ [ 0 , 1 ] \phi\left(A_{r=8}, A_{r=64}, i, j\right)=\frac{\left\|U_{A_{r=8}}^{i \top} U_{A_{r=64}}^j\right\|_F^2}{\min (i, j)} \in[0,1] ϕ(Ar=8,Ar=64,i,j)=min(i,j) UAr=8i⊤UAr=64j F2∈[0,1]
ϕ ( ⋅ ) \phi(·) ϕ(⋅)的范围为[0, 1],1代表子空间完全重叠,0表示完全分离,下图是改变i和j时 ϕ ( ⋅ ) \phi(·) ϕ(⋅)的变化情况。

上图可以发现秩为8和64的top向量之间显著重叠,而其他方向则没有,可能原因是其他方向主要包含训练期间累积的噪声,因此,自适应矩阵确实可以具有非常低的秩。
Subspace similarity between different random seeds
为了进一步证实这一点,作者通过绘制r=64下的两个随机种子的标准化子空间相似度图进行比较,如下图所示:

Δ W q \Delta W_q ΔWq比 Δ W v \Delta W_v ΔWv有更高的内在秩,可以由上图观察得到。
7.3 HOW DOES THE ADAPTATION MATRIX ∆W COMPARE TO W ?
作者进一步探讨 Δ W \Delta W ΔW和 W W W之间的联系,或者从数学角度出发,探索 Δ W \Delta W ΔW是否主要包含在 W W W的主要奇异方向,以及 Δ W \Delta W ΔW与 W W W原始方向相比有多大。作者通过奇异值分解将 W W W投影到 Δ W \Delta W ΔW的r维子空间,接着比较原始 W W W和 U ⊤ W V ⊤ U^{\top}WV^{\top} U⊤WV⊤的F范数,为了进一步对比,还用 W W W的前r个奇异向量或随机矩阵来替换U和V。

上表可以得出如下的结论:
- 与随机矩阵相比, Δ W \Delta W ΔW比 W W W具有更强的相关性;
- Δ W \Delta W ΔW只放大了 W W W中未强调的方向。
- 放大系数相当大(6.91/0.32=21.5)。
此外根据附录的内容,可以表明低秩适应矩阵可能会方法下游任务的重要特征,这些任务是预训练模型中学习到但是没有强调的。
8. CONCLUSION AND FUTURE WORK
LoRA是一种有效的低秩分解策略,既不会引入推理延迟,也不会减少输入序列长度,同时保持模型的性能。未来LoRA的方向可以有如下几点:
- 与其它有效的微调方法相结合。
- 如何让预训练期间学习到的特征在下游任务上表现出色。
- 有没有更严谨的方法找到LoRA的使用模块。
- Δ W \Delta W ΔW的低秩特性表明 W W W本身可能也是低秩的。
阅读总结
一篇21年的关于微调优化的工作,却在大模型盛行的23年又火了一把,我认为有几点重要的原因:
- 原理简单。就是将之前串行的Adapter改成了并行,两层MLP,学习后并入冻结的权重中以推理。
- 优势明显。既不像Adapter需要额外的推理时间,又不像Prefix-tuning占用输入token序列长度。
- 效果显著。通过实验表明,LoRA不输于全量微调。
- 即插即用。训练好的LoRA模块可以直接用在相似的下游任务场景。
- 故事精妙。作者追踪溯源,先提出方法,再探索方法的奥秘。LoRA为什么效果好,是因为大模型微调的本质是参数有效性利用,如何证明参数有效性利用,那就通过实验和计算证明低秩特性,利用了什么样的参数?再通过实验证明放大了预训练中未强调但是在下游任务重要的参数。
虽然在证明上并没有特别严谨,但是整体的思路清晰明了,具有说服力,还是特别值得学习的。这对我也有了一定的启发,做工作不能浮于表面,要往深处看,透过现象看本质,参透本质后,灵感肯定会喷涌而出。